相关试卷

1、计算： $(4 - \sqrt{3})^{0} - 3 t a n 6 0^{°} + (- \frac{1}{2})^{- 2}$ .

查看解析
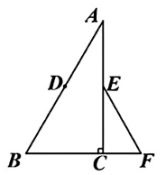
2、如图，在Rt△ABC中，AB=8，∠B=60°，点D，E分别是AB，AC边上的中点，点F
在BC的延长线上，连接EF，∠F=60°.点P从点D出发，沿D→B→F运动到点F，在边EF上找一点Q，连结PQ，使得∠APQ=∠B，则在点P的运动的过程中，点Q的运动路径长为.

查看解析
3、如图，在 $△ A B C$ 中， $∠ A = 9 0^{°}$ ， $t a n B = \frac{1}{2}$ ，点M，N分别在边AB和AC上，且 $∠ A M N = ∠ C$ ，作 $D M ⊥ A B$ 交BC于D， $N E ⊥ A C$ 交BC于E（D在E左侧），若MN上存在一点P，使得 $∠ M D P = ∠ D P E = ∠ P E N = 9 0^{°}$ ，则 $\frac{A M}{A B} =$ .

查看解析
4、如图是某圆锥的主视图和左视图，该圆锥的侧面积是（结果保留π）·

查看解析
5、现将背面相同，正面分别写有“中”、“考”、“必”、“胜”的四张卡片，洗匀后背面朝上放在桌面上，同时抽取两张，则抽取的两张卡片上的文字恰好能组成“必胜”的概率是.

查看解析
6、如图，点A，B，C是⊙O上的三点，若∠BAC=36°，则∠BOC的度数是.

查看解析
7、计算：a²-4b²=.

查看解析
8、如图，点G，H，P，Q分别在等腰 $△ A B C$ 的腰上，连接GH，PQ，已知 $G H ∥ P Q ∥ B C$ ， $A G = B P$ ，且 $s i n A = a s i n B$ ， $P Q + G H = b$ ， AB的长为定值.当a与b发生变化时，下列代数式的值不变的是（）

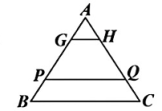A、 $\frac{b}{a}$ B、ab C、a+b D、 $\frac{b}{a^{2}}$

查看解析
9、如图，点D，E，F分别在 $△ A B C$ 的边上， $∠ A F D = ∠ F D E = ∠ D E B$ ，点G是EF的中点，连接AG并延长交BC于点H，已知 $\frac{D F}{B C} = \frac{3}{7}$ ，则 $\frac{B E}{C H}$ 的值是（）

A、 $\frac{40}{21}$ B、 $\frac{4}{3}$ C、 $\frac{7}{3}$ D、 $\frac{49}{30}$

查看解析
10、下列图形不能被边长为4的正方形完全覆盖的是（）

A、半径为2的圆 B、半径为2.5的半圆 C、两边长分别为 $\sqrt{2}$ ， $3 \sqrt{2}$ 的三角形 D、斜边长为5的直角三角形

查看解析
11、已知点 $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ 在反比例函数 $y = - \frac{2}{x}$ 图像上， $x_{1} \neq x_{2}$ .若 $x_{1} \cdot x_{2} < 0$ ，则 $(x_{2} - x_{1}) \cdot (y_{2} - y_{1})$ 的值为（）

A、0 B、正数 C、负数 D、非负数

查看解析
12、端午节是中国的传统节日，某商店销售甲、乙两种礼盒的粽子，经调查发现：用880元购进的甲礼盒数量是用400元购进的乙礼盒数量的2倍，且每个甲礼盒的进价比乙礼盒贵4元，设每个乙礼盒的进价为x元，则下列方程正确的是（）

A、 $2 \times \frac{880}{x - 4} = \frac{400}{x}$ B、 $2 \times \frac{880}{x + 4} = \frac{400}{x}$ C、 $\frac{880}{x - 4} = 2 \times \frac{400}{x}$ D、 $\frac{880}{x + 4} = 2 \times \frac{400}{x}$

查看解析
13、如图，以点O为位似中心的△ABC与△DEF的周长比为2：3，则OA：AD的值是（）

A、4：9 B、3：1 C、2：1 D、2：3

查看解析
14、已知某种彩票的中奖概率为1%，则下列说法正确的是（）

A、买1张彩票，不可能中奖 B、买200张彩票，可能有2张中奖 C、买100张彩票，一定有1张中奖 D、若100人各买1张彩票，一定会有1人中奖

查看解析
15、如图是一个由4个相同的正方体组成的立体图形，它的左视图是（）

A、 B、 C、 D、

查看解析
16、如果温度上升3C记作+3C，那么下降8c记作（）

A、-5℃ B、11° C、C.+8℃ D、-8℃

查看解析
17、如图，AB是 $⊙ O$ 的直径，点 $C$ 在 $⊙ O$ 上，过点 $C$ 作 $C D ⊥ A B$ 交AB于点 $E$ ， $G$ 为 $\overset{⌢}{A D}$ 上的一点，连接AG交CD的延长线于点 $F$ ，连接CG交AB于点 $M$ ，连接DG，MD.

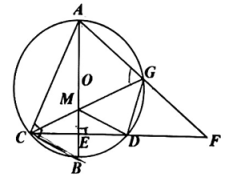(1)、求证：∠AGC=∠DGF.

(2)、设∠MDG=α，∠F=β，∠ACE=γ·
①求证：α=2β.
②若DG=DM，求β和γ的数量关系.

查看解析
18、已知二次函数y=ax²+bx-8a（a，b是常数，a≠0），其图象过点（2，2）.

(1)、用含a的代数式表示b.

(2)、当a=1时，
①若-2≤x≤1时，求二次函数的最大值和最小值。
②若x满足m≤x≤m+3时，二次函数的最小值为2，求m的值.

查看解析
19、根据要求作图并证明.
如图，有一张矩形纸片ABCD，AB=6，AD=10.将纸片进行两次折叠，第一次折叠使得点A与点B重合，复原纸片得到折痕EF；第二次经过点B折叠，使点A的对称点A'落在EF上.得到折痕BG，G为折痕与AD的交点.

(1)、尺规作图：在图中做出点A'及折痕BG（借助无刻度的直尺和圆规、不写作法，保留作图痕迹）·

(2)、连接AA'，A'B，判断△ABA’形状，并证明.

查看解析
20、某校为确保学生安全，开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛，现从七年级和八年级参与竞赛的学生中各随机抽取10名学生的成绩（百分制）进行整理、描述和分析（成绩均不低于70分，用x表示），将学生竞赛成绩分为A，B，C三个等级，A：70≤x<80，B：80≤x<90，C：90≤x≤100.下面给出了部分信息：
七年级10名学生的竞赛成绩为：75，76，85，85，87，87，87，94，96，98.
八年级10名学生的竞赛成绩在B等级中的数据为：82，83，86，89，89.
两组数据的平均数、中位数、众数、方差如下表所示：
学生
平均数
中位数
众数
方差
七年级
87
86
b
52.4
八年级
87
a
89
62.4
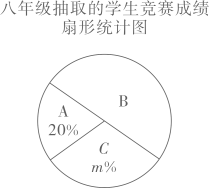
根据以上信息，解答下列问题：

(1)、填空：a= ， b= ， m=.

(2)、根据以上数据，从统计量角度进行分析：哪个年级的成绩更好？请说明理由（一条理由即可）.

(3)、该校七年级共有900人参赛，八年级共有850人参赛，请估计该校七、八年级参赛学生中成绩为“优秀”（x≥90）的总共有多少人?

查看解析

上一页 1026 1027 1028 1029 1030 下一页跳转

学生	平均数	中位数	众数	方差
七年级	87	86	b	52.4
八年级	87	a	89	62.4