-
1、下列计算正确的是( )A、 B、 C、 D、
-
2、已知扇形的半径为6,圆心角为 , 则它的面积是( )A、 B、 C、 D、
-
3、据文化旅游部数据显示,2024年国庆节假期,全国国内出游约1467000000人次,将1467000000个数用科学记数法表示为( )A、 B、 C、 D、
-
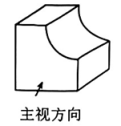
4、如图,该几何体的俯视图是( )
 A、
A、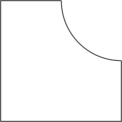 B、
B、 C、
C、 D、
D、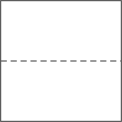
-
5、-2025的绝对值为( )A、2025 B、-2025 C、 D、
-
6、 如图,在矩形中,过A作于点H , 交于点E , 以为直径作与相交于点F , 连接并延长交于点G , 连接并延长交射线于点P .
 (1)、求证:是等腰三角形;(2)、如图1,与相交于点Q , 若点Q为的中点,求的值;(3)、如图2,已知 , , 求的长.
(1)、求证:是等腰三角形;(2)、如图1,与相交于点Q , 若点Q为的中点,求的值;(3)、如图2,已知 , , 求的长. -
7、 在平面直角坐标系中,抛物线 .
 (1)、若 , 抛物线与x轴只有一个交点.
(1)、若 , 抛物线与x轴只有一个交点.①求证:;
②抛物线的顶点为A , 与y轴相交于点B , 直线的表达式为 . 求在范围内,x等于多少时,取得最大值?
(2)、点在该抛物线上, . 若 , 求t的取值范围. -
8、 小明组装了两辆智能机器车进行场地测试,场地内M , N两点相距 , 甲、乙两车先后从M出发沿相同路线驶向N . 设甲车出发行走时间为x(分),两车行走路程y(米)关于x的函数图象如图1所示,两车相距s(米)关于x(分)的函数图象如图2所示.
 (1)、求所在直线的函数表达式;(2)、求点C的坐标,并解释该点的实际意义;(3)、当x为多少时,两车相距n米?
(1)、求所在直线的函数表达式;(2)、求点C的坐标,并解释该点的实际意义;(3)、当x为多少时,两车相距n米? -
9、 如图,在中, , 为的中点, , 分别为 , 上的点,且 , .
 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数. -
10、 为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中信息解答下列问题:

规定:
为增强学生的身体素质,学生每天参加户外活动的平均时间不少于1小时.
(1)、请补全频数分布直方图;(2)、求表示户外活动时间小时的扇形圆心角的度数;(3)、本次调查中,学生参加户外活动的平均时间是否符合要求?试通过计算说明. -
11、 如图,在中, , .
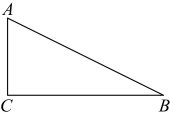 (1)、尺规作图:
(1)、尺规作图:①作的角平分线 , 交于点P;
②作点P到的距离 . (保留作图痕迹,不写作法).
(2)、在(1)的条件下,求的长. -
12、 解不等式: .
小明解答过程如下,请指出其中错误步骤的序号,并写出正确的解答过程.
解:①
②
③
④
-
13、 计算: .
-
14、 如图,在四边形中, , , , . 把四边形的两个角向内折叠,使 , 两点在点处重合,点落在边上的点处, , 是折痕.若 , 则的长度是 .

-
15、 如图是一铺设在人行道上地板砖的一部分,它是由正六边形和四边形镶嵌而成, , , 为各多边形顶点,则的值为 .

-
16、 一无人超市门口的墙AB上装有一个传感器P , 离地面高度 , 当人从门外走到离该传感器及以内时,便自动发出语音“欢迎光临”.身高的小明走到处时,恰好响起“欢迎光临”,则的长为 .

-
17、 某商场在五一期间开展幸运抽奖活动,每个顾客都有奖.下表是奖金等级、金额和中奖人数的分配表:
奖金等级
一等奖
二等奖
三等奖
四等奖
五等奖
奖金额(元)
1000
500
100
20
10
中奖人数
3
8
89
300
600
则中大奖(不低于100元)的概率为 .
-
18、 如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα= ,则t的值是 .

-
19、 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形与正方形 , 射线与的延长线相交于点P . 若 , 则的值是( )
 A、 B、3 C、 D、
A、 B、3 C、 D、 -
20、 如图,点A , B在反比例函数(常数)图象上,作轴于点C , 轴于点D , 过B作于点E , 连接 , , . 则下列三角形中,与的面积一定相等的是( )
 A、 B、 C、 D、
A、 B、 C、 D、