-
1、已知某种彩票的中奖概率为1%,则下列说法正确的是( )A、买1张彩票,不可能中奖 B、买200张彩票,可能有2张中奖 C、买100张彩票,一定有1张中奖 D、若100人各买1张彩票,一定会有1人中奖
-
2、如图是一个由4个相同的正方体组成的立体图形,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
3、如果温度上升3C记作+3C,那么下降8c记作( )A、-5℃ B、11° C、C.+8℃ D、-8℃
-
4、如图,AB是的直径,点在上,过点作交AB于点 , 为上的一点,连接AG交CD的延长线于点 , 连接CG交AB于点 , 连接DG,MD.
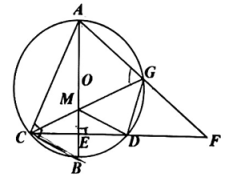 (1)、求证:∠AGC=∠DGF.(2)、设∠MDG=α,∠F=β,∠ACE=γ·
(1)、求证:∠AGC=∠DGF.(2)、设∠MDG=α,∠F=β,∠ACE=γ·①求证:α=2β.
②若DG=DM,求β和γ的数量关系.
-
5、已知二次函数y=ax2+bx-8a(a,b是常数,a≠0),其图象过点(2,2).(1)、用含a的代数式表示b.(2)、当a=1时,
①若-2≤x≤1时,求二次函数的最大值和最小值。
②若x满足m≤x≤m+3时,二次函数的最小值为2,求m的值.
-
6、根据要求作图并证明.
如图,有一张矩形纸片ABCD,AB=6,AD=10.将纸片进行两次折叠,第一次折叠使得点A与点B重合,复原纸片得到折痕EF;第二次经过点B折叠,使点A的对称点A'落在EF上.得到折痕BG,G为折痕与AD的交点.
 (1)、尺规作图:在图中做出点A'及折痕BG(借助无刻度的直尺和圆规、不写作法,保留作图痕迹)·(2)、连接AA',A'B,判断△ABA’形状,并证明.
(1)、尺规作图:在图中做出点A'及折痕BG(借助无刻度的直尺和圆规、不写作法,保留作图痕迹)·(2)、连接AA',A'B,判断△ABA’形状,并证明. -
7、某校为确保学生安全,开展了“远离溺水·珍爱生命”的防溺水安全知识竞赛,现从七年级和八年级参与竞赛的学生中各随机抽取10名学生的成绩(百分制)进行整理、描述和分析(成绩均不低于70分,用x表示),将学生竞赛成绩分为A,B,C三个等级,A:70≤x<80,B:80≤x<90,C:90≤x≤100.下面给出了部分信息:
七年级10名学生的竞赛成绩为:75,76,85,85,87,87,87,94,96,98.
八年级10名学生的竞赛成绩在B等级中的数据为:82,83,86,89,89.
两组数据的平均数、中位数、众数、方差如下表所示:
学生
平均数
中位数
众数
方差
七年级
87
86
b
52.4
八年级
87
a
89
62.4
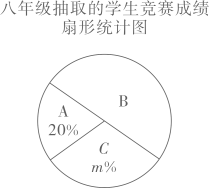
根据以上信息,解答下列问题:
(1)、填空:a= , b= , m=.(2)、根据以上数据,从统计量角度进行分析:哪个年级的成绩更好?请说明理由(一条理由即可).(3)、该校七年级共有900人参赛,八年级共有850人参赛,请估计该校七、八年级参赛学生中成绩为“优秀”(x≥90)的总共有多少人? -
8、如图,在中, , , , 点D在BC边上,且 , , 垂足为E,连结CE
 (1)、求的值.(2)、求的度数.
(1)、求的值.(2)、求的度数. -
9、先化简,再求值: , 其中.
-
10、计算:.
-
11、如图,在菱形ABCD中, , , E是AB边上的一点, , 将四边形AEFD沿着EF折叠得到四边形A'D'FE,当三点A',B,D'在同一条直线上时,°,此时D'F交BC边于点G,CG的长为.

-
12、如图,在平面直角坐标系中,点A(0,4),B(3,4),将向右平移一定距离,得到 , 点F为DE中点,函数的图像经过点C和点F,则k的值是.

-
13、动车组列车的普通坐席位置通常用A,B,C,D,F五个字母表示,其中A,F代表靠窗坐席,小红随机购买了一张动车组列车的普通坐席车票,坐席是靠窗位置的概率为.
-
14、方程组的解为.
-
15、因式分解:a2-6a=.
-
16、如图,在正方形ABCD中,将边AB绕点A逆时针旋转至AF,使F点落在正方形ABCD内部,延长BF交的平分线于点H,连结FD交AH于点G,则下列比值是定值的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、点 , , 在反比例函数的图象上,且 , 则下列判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
18、如图,在中,分别以这个三角形的三边为边长向外侧作正方形,其面积分别记为 , , .若 , 则图中阴影部分的面积为( )
 A、6 B、 C、5 D、
A、6 B、 C、5 D、 -
19、小鹿两次购买相同药物的费用均为200元,第二次购买时每盒降价8元,他多买了2盒.设第一次购买时该药品的单价为x(元/盒),则可列方程为( )A、 B、 C、 D、
-
20、如图,与位似,位似中心为点O,OC':OC=3:4,的面积为9,则面积为( )
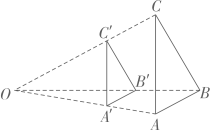 A、12 B、 C、16 D、18
A、12 B、 C、16 D、18