相关试卷

1、如图，在 $R t △ A B C$ 中， $A B = 3$ ， $A C = 5$ ，以点C为圆心， $\sqrt{10}$ 为半径作圆.点D为边AB上的动点，DP，DQ分别切圆C于点P，点Q，连接PQ，分别交AC和BC于点E，F，取PQ的中点M.

(1)、当 $∠ P D Q = 6 0^{°}$ 时，求劣弧PQ的度数；

(2)、当 $C E = C F$ 时，求AD的长；

(3)、连接CM，BM.
①证明： $M E \cdot C A = C M \cdot A D$ .
②在点D的运动过程中，BM是否存在最小值？若存在，直接写出BM的值；若不存在，请说明理由.

查看解析
2、已知点（1，2）在抛物线 $y_{1} = x^{2} + 2 b x + c$ （b，c为常数）的图象上.

(1)、用含b的代数式表示c；

(2)、当b的值变化时， $y_{1} = x^{2} + 2 b x + c$ 的顶点总在另一抛物线 $y_{2} = - x^{2} + p x + q$ 的图象上，
①求p，q的值；
②若抛物线 $y_{1} = x^{2} + 2 b x + c$ 和抛物线 $y_{2} = - x^{2} + p x + q$ 围成的封闭区域内（不包含边界）有且只有2个横纵坐标均为整数的点，求b的取值范围.

查看解析
3、在一条直线上依次有A、B、C三个海岛，某海巡船从A岛出发沿直线匀速经B岛驶向C岛，执行海巡任务，最终到达C岛，设该海巡船行驶x（h）后，与B港的距离为y（km），已知y与x的函数图象如图所示.

(1)、填空：A、C两海岛间的距离为km，a=；

(2)、求线段PN所表示的函数关系式；

(3)、在B岛有一不间断发射信号的信号发射台，发射的信号覆盖半径为15km，求该海巡船能接收到该信号的时间有多长.

查看解析
4、如图为正六边形ABCDEF，请仅用无刻度的直尺按要求完成以下作图（保留作图痕迹），

(1)、在图1的正六边形ABCDEF内部作一点M，连接AM，使得∠BAM=60°.

(2)、在图2的正六边形ABCDEF内部作一点N，连接AN，使得tan∠BAN= $\frac{\sqrt{3}}{2}$

查看解析
5、如图，矩形ABCD的对角线AC，BD相交于点O，DEllAC，CEllBD.

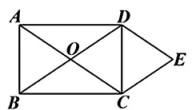(1)、求证：四边形OCED为菱形；

(2)、若AB=3，AC=5，求菱形OCED的面积.

查看解析
6、2025年央视春晚中的《秧BOT》节目标志着我国人工智能的飞速发展.某校为了解学生对人工智能知识的掌握程度，组织相同人数的甲、乙两个科技小组进行一场人工智能知识竞赛，分别绘制了成绩不完整的甲组成绩统计表和乙组成绩统计图如下，并进行公布（满分10分，分数取整数）·
甲组成绩统计表
分数
7分
8分
9分
10分
人数
10
1
2
m

(1)、求甲组成绩统计表中m的值，并将乙组成绩条形统计图补充完整；

(2)、求甲组学生成绩的平均分和中位数；

(3)、成绩公布后，老师发现甲组一名学生成绩登记错误，若将该生成绩修改正确，甲组的位数会超过乙组的中位数，直接写出这名学生至少增加多少分。

查看解析
7、先化简，再求值： $(\frac{a}{a - 1} - 1) \div \frac{a^{2} + a}{a^{2} - 1}$ ，其中 $a = \frac{5}{2}$ .

查看解析
8、计算： $(4 - \sqrt{3})^{0} - 3 t a n 6 0^{°} + (- \frac{1}{2})^{- 2}$ .

查看解析
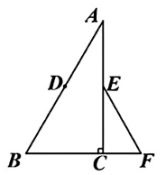
9、如图，在Rt△ABC中，AB=8，∠B=60°，点D，E分别是AB，AC边上的中点，点F
在BC的延长线上，连接EF，∠F=60°.点P从点D出发，沿D→B→F运动到点F，在边EF上找一点Q，连结PQ，使得∠APQ=∠B，则在点P的运动的过程中，点Q的运动路径长为.

查看解析
10、如图，在 $△ A B C$ 中， $∠ A = 9 0^{°}$ ， $t a n B = \frac{1}{2}$ ，点M，N分别在边AB和AC上，且 $∠ A M N = ∠ C$ ，作 $D M ⊥ A B$ 交BC于D， $N E ⊥ A C$ 交BC于E（D在E左侧），若MN上存在一点P，使得 $∠ M D P = ∠ D P E = ∠ P E N = 9 0^{°}$ ，则 $\frac{A M}{A B} =$ .

查看解析
11、如图是某圆锥的主视图和左视图，该圆锥的侧面积是（结果保留π）·

查看解析
12、现将背面相同，正面分别写有“中”、“考”、“必”、“胜”的四张卡片，洗匀后背面朝上放在桌面上，同时抽取两张，则抽取的两张卡片上的文字恰好能组成“必胜”的概率是.

查看解析
13、如图，点A，B，C是⊙O上的三点，若∠BAC=36°，则∠BOC的度数是.

查看解析
14、计算：a²-4b²=.

查看解析
15、如图，点G，H，P，Q分别在等腰 $△ A B C$ 的腰上，连接GH，PQ，已知 $G H ∥ P Q ∥ B C$ ， $A G = B P$ ，且 $s i n A = a s i n B$ ， $P Q + G H = b$ ， AB的长为定值.当a与b发生变化时，下列代数式的值不变的是（）

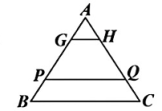A、 $\frac{b}{a}$ B、ab C、a+b D、 $\frac{b}{a^{2}}$

查看解析
16、如图，点D，E，F分别在 $△ A B C$ 的边上， $∠ A F D = ∠ F D E = ∠ D E B$ ，点G是EF的中点，连接AG并延长交BC于点H，已知 $\frac{D F}{B C} = \frac{3}{7}$ ，则 $\frac{B E}{C H}$ 的值是（）

A、 $\frac{40}{21}$ B、 $\frac{4}{3}$ C、 $\frac{7}{3}$ D、 $\frac{49}{30}$

查看解析
17、下列图形不能被边长为4的正方形完全覆盖的是（）

A、半径为2的圆 B、半径为2.5的半圆 C、两边长分别为 $\sqrt{2}$ ， $3 \sqrt{2}$ 的三角形 D、斜边长为5的直角三角形

查看解析
18、已知点 $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ 在反比例函数 $y = - \frac{2}{x}$ 图像上， $x_{1} \neq x_{2}$ .若 $x_{1} \cdot x_{2} < 0$ ，则 $(x_{2} - x_{1}) \cdot (y_{2} - y_{1})$ 的值为（）

A、0 B、正数 C、负数 D、非负数

查看解析
19、端午节是中国的传统节日，某商店销售甲、乙两种礼盒的粽子，经调查发现：用880元购进的甲礼盒数量是用400元购进的乙礼盒数量的2倍，且每个甲礼盒的进价比乙礼盒贵4元，设每个乙礼盒的进价为x元，则下列方程正确的是（）

A、 $2 \times \frac{880}{x - 4} = \frac{400}{x}$ B、 $2 \times \frac{880}{x + 4} = \frac{400}{x}$ C、 $\frac{880}{x - 4} = 2 \times \frac{400}{x}$ D、 $\frac{880}{x + 4} = 2 \times \frac{400}{x}$

查看解析
20、如图，以点O为位似中心的△ABC与△DEF的周长比为2：3，则OA：AD的值是（）

A、4：9 B、3：1 C、2：1 D、2：3

查看解析

上一页 1022 1023 1024 1025 1026 下一页跳转

分数	7分	8分	9分	10分
人数	10	1	2	m