-
1、DeepSeek是一款基于人工智能技术的深度搜索工具,从“DeepSeek”中随机抽取一个字母,抽中字母“e”的概率是.
-
2、如图,用4个全等的 , , , 和2个全等的 , 拼成如图所示的矩形ABCD,则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、已知二次函数y=ax2+bx+c(a≠0)的图象经过点M(-2,m),N(4,n),若m<n,则下列可能成立的是( )A、当a>0时,a+b=0 B、当a>0时,2a+b=0 C、当a<0时,a+b=0 D、当a<0时,2a-b=0
-
4、在AABC中,点D,E分别是AB,AC的中点,如图是甲、乙两位同学添辅助线的作法:
甲同学:如图1,延长DE到点F,使EF=DE,连接DC,AF,FC.

乙同学:如图2,过点E作GE//AB,过点A作AF//BC,GE与AF交于点F.

其中能够用来证明三角形中位线定理的是( )
A、甲、乙都可以 B、甲、乙都不可以 C、甲可以,乙不可以 D、甲不可以,乙可以 -
5、中国古代数学名著《九章算术》第八卷《方程》中一道名题,大意如下:今有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平,并燕、雀重一斤,问燕、雀一枚各重几何?译文为:“今有5只雀、6只燕,分别聚集而且用衡器称之,聚在一起的雀重,燕轻.将一只雀、一只燕交换位置而放,重量相等.5只雀、6只燕重量共为1斤.问雀、燕每只各多重?”现设每只雀x斤,每只燕y斤,则可列出方程组( )A、 B、 C、 D、
-
6、如图,△ABC是⊙O的内接三角形,连接OB,OC,若∠BAC+∠BOC=84°,则∠BOC的度数为( )
 A、28° B、48° C、56° D、60°
A、28° B、48° C、56° D、60° -
7、在体育中考“排球垫球”项目中,某校某小组的5位学生垫球次数如下:70、71、74、74、72,则这组数据的中位数为( )A、70 B、71 C、72 D、74
-
8、一个几何体的三视图如图所示,那么这个几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
9、经文化和旅游部数据中心测算,2025年“五一”假期全国国内出游3.14亿人次.其中数据“3.14亿”用科学记数法表示为( )A、 B、 C、 D、
-
10、下列各式运算正确的是( )A、 B、 C、 D、
-
11、的相反数是( )A、 B、 C、 D、
-
12、如图1,在平面直角坐标系中,抛物线与x轴交于点 , , 交y轴于点C.
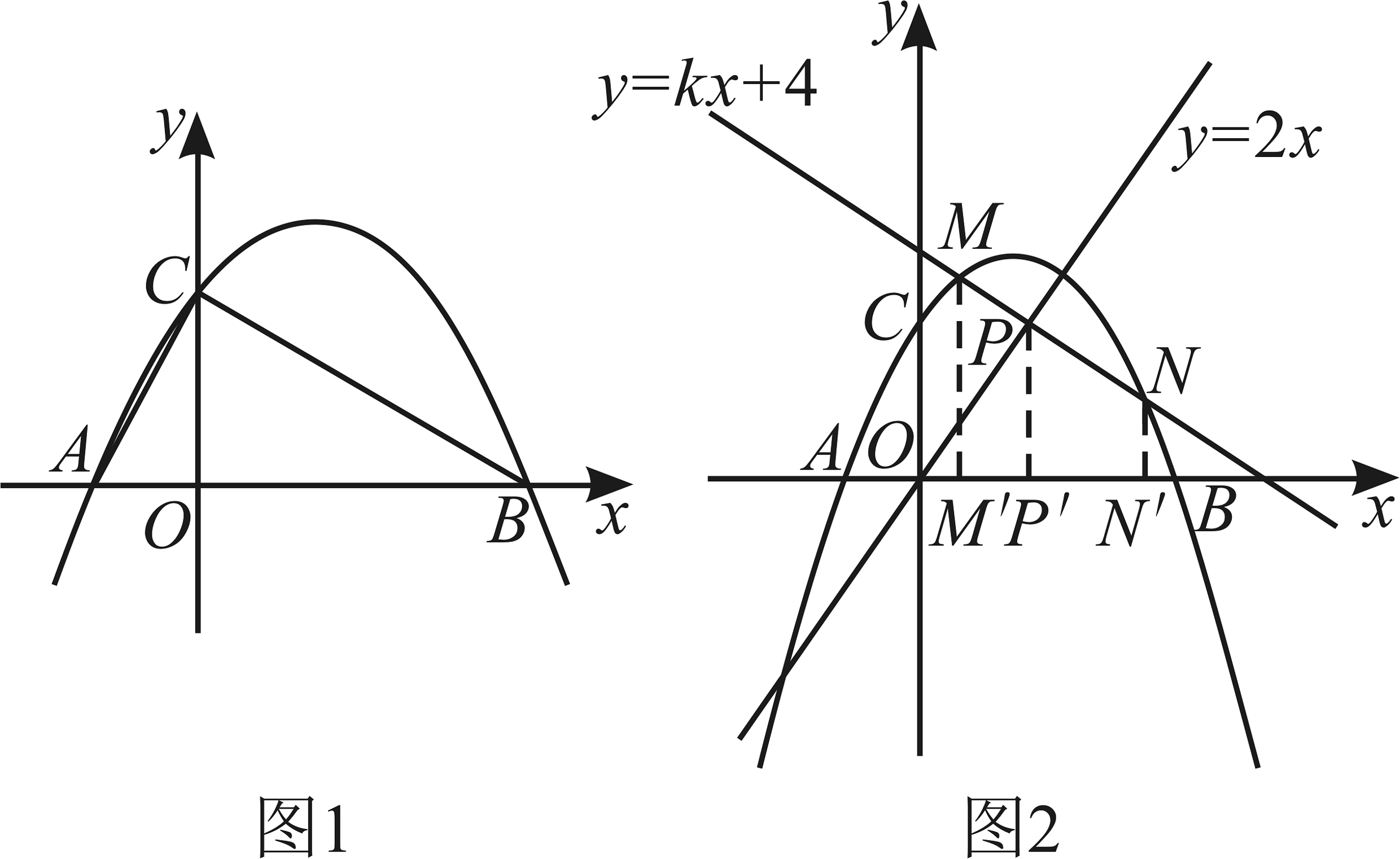 (1)、求抛物线的解析式;(2)、点D为抛物线上一点.若 , 求点D的坐标;(3)、如图2,一次函数与抛物线交于M,N两点,与直线交于P点,分别过点M,N,P作x轴的垂线,其垂足依次为点 , , , 若 , 求m的值.
(1)、求抛物线的解析式;(2)、点D为抛物线上一点.若 , 求点D的坐标;(3)、如图2,一次函数与抛物线交于M,N两点,与直线交于P点,分别过点M,N,P作x轴的垂线,其垂足依次为点 , , , 若 , 求m的值. -
13、近期,学校开展“书香校园”活动,阅览室又购进了一批优质读物.为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成统计图表.

借阅图书的次数
0
1
2
3
4
人数
7
13
a
10
3
请你根据统计图表中的信息,解答下列问题.
(1)、 ________, ________;(2)、求抽取的部分学生一周内平均每人借阅图书的次数;(3)、该校大概有5000名学生,根据调查结果,估计学生在一周内借阅图书“3次及3次以上”的人数. -
14、今年春晚,秧的特别表演惊艳了所有的观众,它的成功无疑是一次科技与人文的璀璨碰撞.高精度激光雷达、深度相机、激光技术等先进技术,实现了实时捕捉环境数据、毫米级空间定位等功能,从而确保了舞蹈动作的精准匹配和协同一致.这不仅展示了机器人在运动控制方面的卓越能力,更体现了科技在文化传承与创新中的重要作用.
活动主题
测试机器人宇树爬坡(坡角)的能力
测量工具
尺、测角仪、计算器等
活动过程
模型抽象

测量方案与数据信息
①机器人的小腿的长度为 , 大腿上点与点的连线与水平面垂直;
②坡角;
③当机器人行走至点时,测得小腿与斜坡的夹角 , 大腿与小腿的夹角 , ;
④参考数据: .
请根据表格中提供的信息,解决下列问题:
(1)、求点到水平面的距离;(2)、计算大腿的长度(结果精确到) -
15、如图,为的内接三角形,其中是的直径.以点为圆心,以任意长为半径画弧,交于点 , 交于点;以点为圆心,以的长为半径画弧,交于点;以点为圆心,以的长为半径画弧,交前弧于点;过点作射线 , 交的延长线于点 .
 (1)、求证:是的切线;(2)、若 , , 求的半径.
(1)、求证:是的切线;(2)、若 , , 求的半径. -
16、当今社会,“直播带货”已经成为商家的一种新型的促销手段.小亮在直播间销售一种进价为每件元的日用商品,经调查发现,该商品每天的销售量(件)与销售单价(元)满足一次函数关系,它们的关系如下表:
销售单价(元)
销售量(件)
(1)、求与之间的函数关系式;(2)、该商家每天想获得元的利润,应将销售单价定为多少元? -
17、计算: .
-
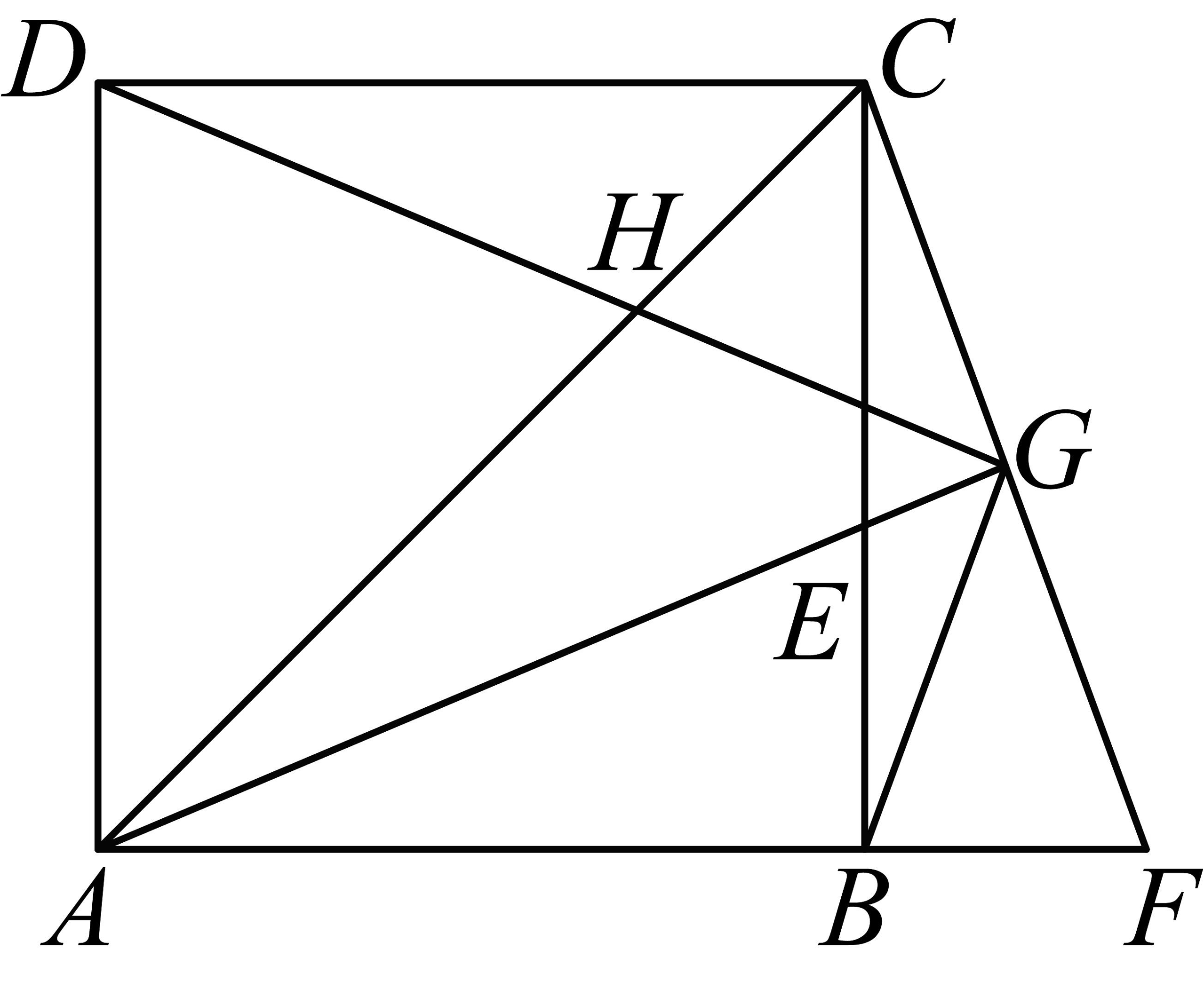
18、如图,四边形为正方形,的平分线交于点 , 将绕点顺时针旋转得到 , 延长交于点 , 连接 , , 与相交于点 . 有下列结论:
①;②;③;④ .
其中正确的是 .
-
19、方程的解是 .
-
20、湖南是著名的吃货大省,“臭豆腐”、“口味虾”、“酱板鸭”、“茶颜悦色”更是声名远扬.若随机从上面美食中选择一种进行品尝,则选中“茶颜悦色”的概率是 .