-
1、如图，在菱形ABCD中，∠A=60°，E，F分别是AB，BC上的动点，连结DF，EF，点M，N分别为DF，EF的中点，则MN的最小值是（ ）
A、 B、 C、1 D、2 -
2、中国古代的《孙子兵法》中记载了一道广为人知的数学问题：现有一百匹马，一百片瓦，大马一匹可以驮三片瓦，小马三匹可以驮一片瓦，问有多少匹大马和多少匹小马？设有大马x匹，小马y匹，则下列方程正确的是（ ）A、 B、 C、 D、
-
3、如图，四边形ABCD与四边形EFGH关于点O位似，且.若四边形ABCD的面积为3，则四边形EFGH的面积为（ ）
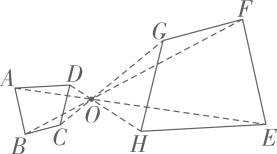A、 B、6 C、12 D、18 -
4、不等式组的所有整数解之和是（ ）A、12 B、13 C、16 D、18
-
5、某班组织一场AI知识竞赛，其中参赛的6名同学得分分别为：72，75，80，78，82，76，则这组数据的中位数是（ ）A、76 B、77 C、78 D、80
-
6、下列各式运算中结果是的是（ ）A、 B、 C、 D、
-
7、由6个大小相同的正方体搭成的几何体如图所示，其主视图是（ ）
A、
B、
C、
D、
-
8、根据温州市统计局发布的《2024年温州市人口主要数据公报》，鹿城区常住人口总量达985.2万人，则985.2万用科学记数法可表示为（ ）A、 B、 C、 D、
-
9、在圆内接四边形ABCD中，AB为直径，D为半圆弧AB的中点，连接AC.
(1)、如图1，①求的度数；
②求证：；
(2)、如图2，过点C作交AB于点E，若 ， 求的值. -
10、已知抛物线у=-x2+bx-3（b为常数）.(1)、若该函数的图象经过（1，0）
①求该二次函数的表达式；
②将该二次函数的图象向右平移m（m>0）个单位长度，得到新的二次函数的图象，若新二次函数的图象的顶点恰好落在直线y=x-3上，求m的值；
(2)、若点P（n，a），Q（n+2，a），M（-2，t）都在这个二次函数图象上，且-3<t<a，求n的取值范围. -
11、载人飞艇已在绍兴及周边区域试飞，未来人们出行将更加便捷，现有甲艇从杭州站经绍兴站飞向宁波站：乙艇从宁波站经绍兴站飞向杭州站，三站均在同一直线上，如图1所示：
两艇同时出发，匀速飞行，图2是甲、乙两艇飞行离绍兴站的距离y（km）与飞行时间x（h）之间的函数图象.
(1)、填空：a的值为；m的值为.(2)、求乙艇离绍兴站的距离y与飞行时间x（0≤x≤3）之间的函数表达式；(3)、乙艇到达杭州站前，两艇与绍兴站的距离之和不超过100km时，求飞行时间x的取值范围. -
12、小张和小李分别完成一个作图问题：
如图1，在□ABCD中，AB<BC，P是边BC上一点，连结AP.利用适当的作图工具在边AD上作一点Q，使得CQIIAP.
小张：如图1，以A为圆心，PC长为半径画弧，交AD于点Q，连结CQ即为所求
小李：我的方法和你不一样，只用无刻度直尺且不用圆规就可以完成作图，……
(1)、给出小张作法中CQIIAP的证明过程；(2)、请在图2中完成小李的作图方法（保留作图痕迹） -
13、某校课外兴趣小组对五一学生外出参加科技馆活动使用交通工具的情况，进行了随机抽样的调查，调查后发现学生选用A、B、C、D四种交通工具的其中一种.A表示乘坐地铁出行，B表示乘坐私家车出行，C表示乘坐公交车出行，D表示公享单车出行或其他，划分类别后的数据整理如下表：
学生外出参加科技馆活动使用交通工具统计表与扇形统计图
类别
人数
比率
A
15
a
B
20
b
C
12
c
D
d
0.06
(1)、求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数；(2)、若该校有1600名学生，估计该校学生中类别为A的人数 -
14、如图，已知菱形ABCD，∠DAB=120°，延长AC至点F，连接DF，∠FDA=90°，延长BC交DF于点E.
(1)、求证：BD=DF；(2)、若AD=1，求△BDE的面积. -
15、解不等式组：
-
16、计算：.
-
17、如图，在△ABC中，AB=AC，过点A作AD⊥AC，交BC于点D，点F是AB上的点，且满足DB=DF，连接CF，若AC=5，CF=6，则CD=.
-
18、如图，在平面直角坐标系中，平行四边形OABC的边AB与反比例函数（k为常数， ， ）的图象交于A，D两点，且与y轴正半轴交于点B，点C在反比例函数（）的图象上，若点D是AB的中点，则k的值为.
-
19、一副三角板ABC和CDE按如图方式摆放，其中∠BAC=∠DCE=90°，∠D=30°，∠B=45°，点A恰好落在DE上，且BC//DE，则∠ACE的度数为.
-
20、已知点P是线段AB的黄金分割点，且AP>PB，若AB=2，则AP=.