相关试卷

1、如图，在平面直角坐标系中，每个正方形小方格的边长都是一个单位长度， $△ A B C$ 的三个顶点 $A (- 1, 1)$ ， $B (- 4, 2)$ ， $C (- 3, 4)$ 均在格点上．

(1)、将 $△ A B C$ 向下平移4个单位长度，请你画出平移后得到的 $△ A_{1} B_{1} C_{1}$ ；

(2)、将 $△ A B C$ 绕点O顺时针旋转 $90 °$ 后得到的 $△ A_{2} B_{2} C_{2}$ ，请你画出 $△ A_{2} B_{2} C_{2}$ ；

(3)、在（2）的条件下，求点C运动路径的长．

查看解析
2、（1）计算： $\sqrt{4} \div {(\frac{1}{2})}^{0} + 5 \times (- 1)$ ；
（2）解不等式组： $\{\begin{array}{l} 3 x \geq x + 2 \\ \frac{2 x + 5}{3} - 1 > x \end{array}$

查看解析
3、如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $B C = 4$ ，点D是 $A C$ 边的中点，点E是 $A C$ 上的动点，连接 $D E$ ，将 $△ A D E$ 沿 $D E$ 翻折得到 $△ A^{'} D E$ ，连结 $A^{'} B$ ，则 $A^{'} B$ 的最小值为．

查看解析
4、如图，在平面直角坐标系中，一次函数 $y_{1} = k x + b$ 的图象与反比例函数 $y_{2} = \frac{m}{x}$ 的图象交于点 $A$ 和 $B$ ．则关于 $x$ 方程 $k x - b = \frac{m}{x}$ 的解是（）

A、 $x_{1} = 1$ ， $x_{2} = 5$ B、 $x_{1} = - 1$ ， $x_{2} = 5$ C、 $x_{1} = 1$ ， $x_{2} = - 5$ D、 $x_{1} = - 1$ ， $x_{2} = - 5$

查看解析
5、随着电影《哪吒2之魔童闹海》的热映，与之相关某漫画册的销量也急剧上升．某书店分两次购进该漫画册共3500套，第二次的总价比第一次多20000元，且两次进价都是40元/套．设该书店第一次购进x套，第二次购进y套，根据题意，所列方程组正确的是（）

A、 $\{\begin{array}{l} x + y = 3500 \\ 40 x - 40 y = 20000 \end{array}$ B、 $\{\begin{array}{l} x = 3500 + y \\ 40 y - 40 x = 20000 \end{array}$ C、 $\{\begin{array}{l} x = 3500 - y \\ 40 y - 40 x = 20000 \end{array}$ D、 $\{\begin{array}{l} x + y = 3500 \\ 40 x - 20000 = 40 y \end{array}$

查看解析
6、下列计算正确的是（）

A、 ${(a^{3})}^{4} = a^{7}$ B、 ${(a + 1)}^{2} = a^{2} + 1$ C、 $3 a + 2 a = 5 a^{2}$ D、 $a^{3} \cdot a^{5} = a^{8}$

查看解析
7、如图， $A B$ 是 $⊙ O$ 的直径，若 $∠ C = 30 °$ ，则 $∠ A O D$ 的度数是（）

A、 $30 °$ B、 $60 °$ C、 $90 °$ D、 $120 °$

查看解析
8、已知关于x的一元二次方程 $x^{2} + 2 x + m = 0$ 有两个不相等的实数根，则m的取值范围是（）

A、 $m < 1$ B、 $m > 1$ C、 $m < 2$ D、 $m > 2$

查看解析
9、小亮的衣柜里有3件上衣，其中有1件是黄色和2件是蓝色，从中任意取出一件正好是蓝色的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{5}$ C、 $\frac{2}{3}$ D、 $\frac{2}{5}$

查看解析
10、如图，已知直线a，b被直线c所截，则 $∠ 1$ 的同位角是（）

A、 $∠ 2$ B、 $∠ 3$ C、 $∠ 4$ D、 $∠ 5$

查看解析
11、若 $x = 2$ 是关于x的方程 $x + a = - 1$ 的解，则a的值是（）

A、 $- 3$ B、0 C、2 D、3

查看解析
12、下列交通指示标志的图案是轴对称图形的是（）

A、 B、 C、 D、

查看解析
13、国家能源局发布数据，截至2024年底，全国累计发电装机容量约为3350000000千瓦，将3350000000用科学记数法表示为（）

A、 $3.35 \times 10^{8}$ B、 $33.5 \times 10^{8}$ C、 $3.35 \times 10^{9}$ D、 $3.35 \times 10^{10}$

查看解析
14、下列图形是平面图形的是（）

A、 B、 C、 D、

查看解析

15、5月中旬，樱桃相继成熟，果农们迎来了繁忙的采摘销售季．为了解樱桃的收益情况，从第1天销售开始，小明对自己家的两处樱桃园连续15天的销售情况进行了统计与分析：

A樱桃园

第x天的单价、销售量与x的关系如下表：

	单价（元/盒）	销售量（盒）
第1天	50	20
第2天	48	30
第3天	46	40
第4天	44	50
…	…	…
第x天		10x+10

第x天的单价与x近似地满足一次函数关系，已知每天的固定成本为745元．

B樱桃园

第x天的利润 $y_{2}$ （元）与x的关系可以近似地用二次函数 $y_{2} = a x^{2} + b x + 25$ 刻画，其图象如图：

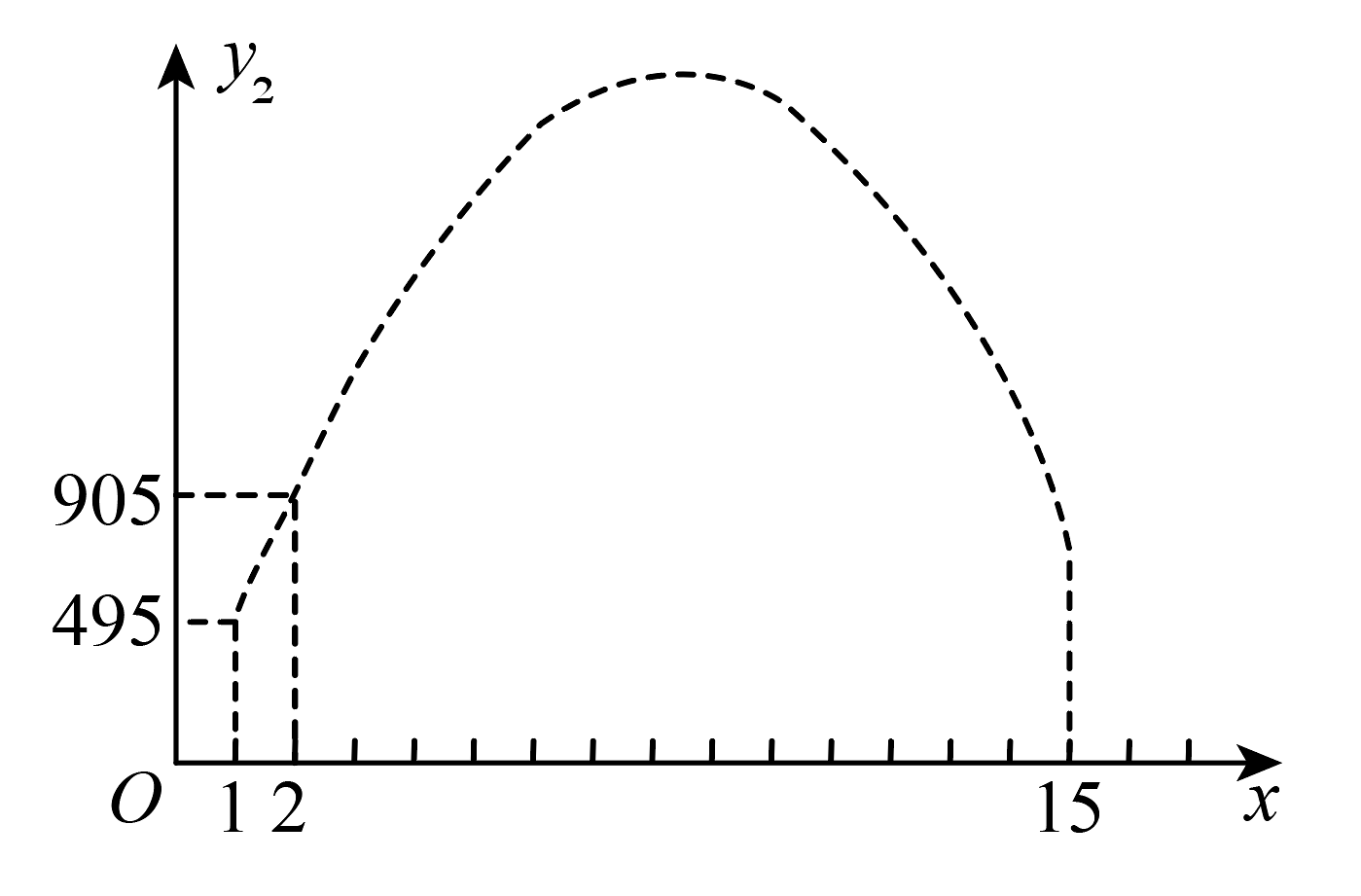(1)、A樱桃园第x天的单价是______元/盒（用含x的代数式表示）；

(2)、求A樱桃园第x天的利润

y_{1}

（元）与x的函数关系式；（利润

=

单价

\times

销售量

-

固定成本）

(3)、①

y_{2}

与x的函数关系式是______；

②求第几天两处樱桃园的利润之和（即 $y_{1} + y_{2}$ ）最大，最大是多少元？

(4)、这15天中，共有______天B樱桃园的利润

y_{2}

比A樱桃园的利润

y_{1}

大．

查看解析

16、如图，在四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O， $∠ A B D = ∠ C D B$ ， $B E ⊥ A C$ 于点E， $D F ⊥ A C$ 于点F，且 $B E = D F$ ．

(1)、求证：四边形 $A B C D$ 是平行四边形；

(2)、若 $A B = B O$ ，当 $∠ A B E$ 等于多少度时，四边形 $A B C D$ 是矩形？请说明理由，并直接写出此时 $\frac{B C}{A B}$ 的值．

查看解析
17、如图，点 $A_{1}, A_{2}, A_{3}, \dots, A_{n}, A_{n + 1}$ 为反比例函数 $y = \frac{k}{x} (k > 0)$ 图象上的点，其横坐标依次为 $1, 2, 3, \dots, n, n + 1$ ．过点 $A_{1}, A_{2}, A_{3}, \dots, A_{n}$ 作x轴的垂线，垂足分别为点 $H_{1}, H_{2}, H_{3}, \dots, H_{n}$ ；过点 $A_{2}$ 作 $A_{2} B_{1} ⊥ A_{1} H_{1}$ 于点 $B_{1}$ ，过点 $A_{3}$ 作 $A_{3} B_{2} ⊥ A_{2} H_{2}$ 于点 $B_{2}$ ， …，过点 $A_{n + 1}$ 作 $A_{n + 1} B_{n} ⊥ A_{n} H_{n}$ 于点 $B_{n}$ ．记 $△ A_{1} B_{1} A_{2}$ 的面积为 $S_{1}, △ A_{2} B_{2} A_{3}$ 的面积为 $S_{2}, \cdot \cdot \cdot, △ A_{n} B_{n} A_{n + 1}$ 的面积为 $S_{n}$ ．

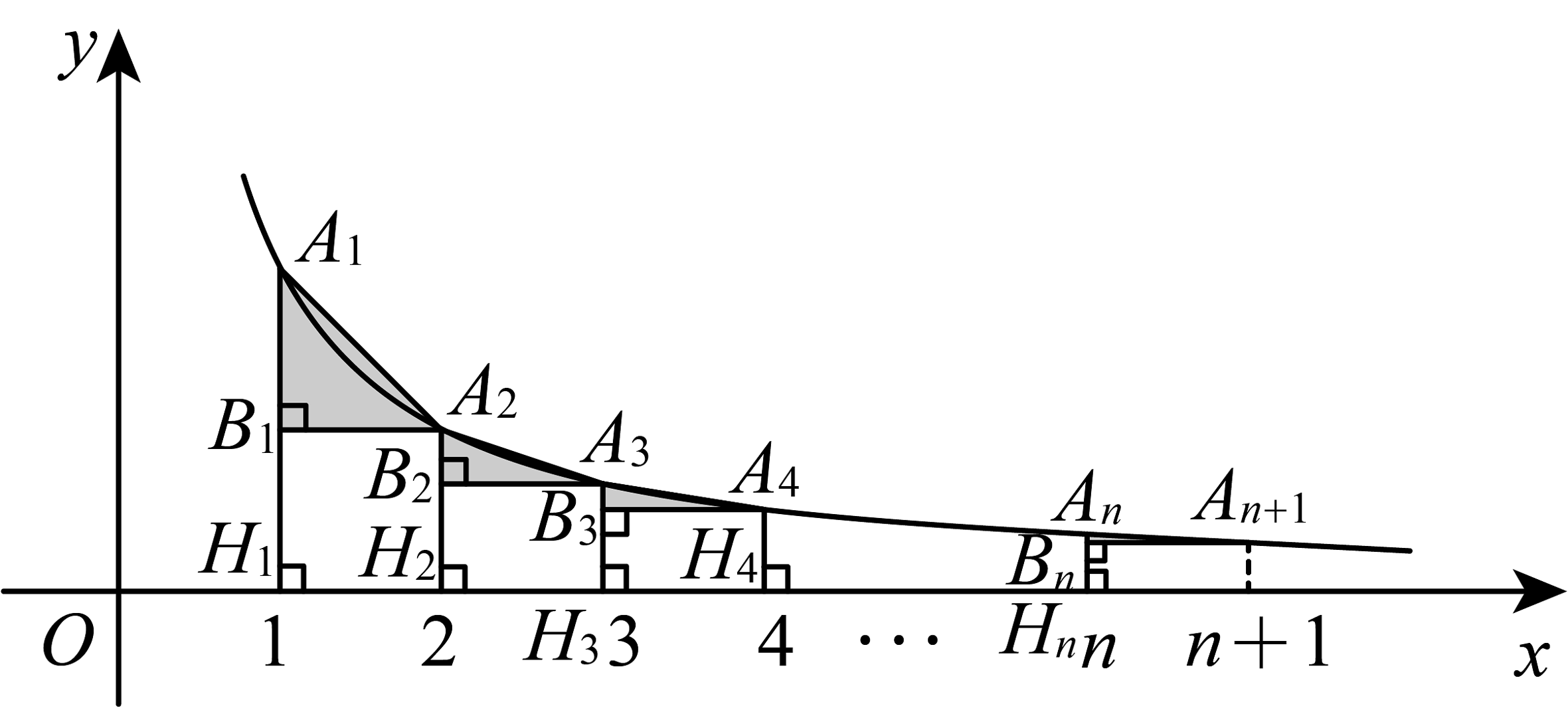(1)、当 $k = 2$ 时，点 $B_{1}$ 的坐标为______， $S_{1} + S_{2} =$ ______， $S_{1} + S_{2} + S_{3} =$ ______， $S_{1} + S_{2} + S_{3} + \dots + S_{n} =$ ______（用含n的代数式表示）；

(2)、当 $k = 3$ 时， $S_{1} + S_{2} + S_{3} + \dots + S_{n} =$ ______（用含n的代数式表示）．

查看解析

18、“滑滑梯”是同学们小时候经常玩的游戏，滑梯的坡角越小，安全性越高．从安全性及适用性出发，小亮同学对所在小区的一处滑梯进行调研，制定了如下改造方案，请你帮小亮解决方案中的问题．

方案名称	滑梯安全改造
测量工具	测角仪、皮尺等
方案设计	如图，将滑梯顶端 $B C$ 拓宽为 $B E$ ，使 $C E = 1 m$ ，并将原来的滑梯 $C F$ 改为 $E G$ ，（图中所有点均在同一平面内，点 $B, C, E$ 在同一直线上，点 $A, D, F, G$ 在同一直线上）
测量数据	【步骤一】利用皮尺测量滑梯的高度 $C D = 1.8 m$ ；【步骤二】在点 $F$ 处用测角仪测得 $∠ C F D = 42 °$ ；【步骤三】在点 $G$ 处用测角仪测得 $∠ E G D = 32 °$ ．
解决问题	调整后的滑梯会多占多长一段地面？（即求 $F G$ 的长）

（参考数据： $\sin 32 ° \approx \frac{17}{32}, \cos 32 ° \approx \frac{17}{20}, \tan 32 ° \approx \frac{5}{8}, \sin 42 ° \approx \frac{27}{40}, \cos 42 ° \approx \frac{3}{4}, \tan 42 ° \approx \frac{9}{10}$ ）

查看解析

19、某校准备开展“行走的课堂，生动的教育”研学活动，并计划从博物馆、动物园、植物园、海洋馆（依次用字母A，B，C，D表示）中选择一处作为研学地点．为了解学生的选择意向，学校随机抽取部分学生进行调查，整理绘制了如下不完整的条形统计图和扇形统计图．
根据以上信息，解答下列问题：

(1)、补全条形统计图；扇形统计图中A所对应的圆心角的度数为______°；

(2)、该校共有1600名学生，请你估计该校有多少名学生想去海洋馆；

(3)、根据以上数据，学校最终将海洋馆作为研学地点，研学后，学校从八年级各班分别随机抽取10名学生开展海洋知识竞赛．甲班10名学生的成绩（单位：分）分别是：75，80，80，82，83，85，90，90，90，95；乙班10名学生的成绩．（单位：分）的平均数、中位数、众数分别是：84，83，88．根据以上数据判断______班的竞赛成绩更好．（填“甲”或“乙”）

查看解析
20、（ $1$ ）解不等式组： $\{\begin{array}{l} \frac{x - 1}{2} \leq 1 \\ x < 3 (x + 2) \end{array}$ ；
（ $2$ ）先化简 $(\frac{a^{2} + 1}{a} - 2) \div \frac{a^{2} - 1}{a}$ ，再从 $- 2$ ， $0$ ， $3$ 中选一个合适的数作为 $a$ 的值代入求值．

查看解析

上一页 1017 1018 1019 1020 1021 下一页跳转