相关试卷

1、如图，在 $△ A B C$ 中， $∠ A C B = 120 °$ ， $A C = B C = 4$ ， $E$ 是边 $B C$ 上的一点， $F$ 是 $B C$ 延长线上的一点， $G$ 为 $A F$ 的中点，连接 $E G$ ．若 $C F = 2 B E$ ，则 $tan ∠ G E F$ 的值为．

查看解析
2、若点 $P (a, - 4)$ 和点 $Q (b, - 2)$ 都在反比例函数 $y = \frac{k + 2}{x}$ 的图象上，且 $a < b$ ，则 $k$ 的值可以是．

查看解析
3、下列运算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 $2 x^{2} \cdot x^{3} = 2 x^{5}$ C、 ${(x - 2)}^{2} = x^{2} - 4$ D、 ${(x^{3})}^{4} = x^{7}$

查看解析
4、已知抛物线 $y = a x^{2} + b x + 1$ 经过 $(- 1, - 4)$ 和 $(2, 5)$ 两点．

(1)、求该抛物线的函数表达式；

(2)、若点 $A$ 为第一象限内该抛物线上的一动点，且在直线 $l ： y = 2 x - 2$ 的上方，过点 $A$ 作 $A B ⊥ x$ 轴于点 $B$ ，交直线 $l$ 于点 $C$ ，以 $A C$ 为直径作 $⊙ N$ ．
①如图1，当 $⊙ N$ 与 $y$ 轴相切时，求点 $A$ 的坐标；
②如图2，直线 $l$ 与 $x$ 轴交于点 $D$ ， $⊙ N$ 交直线 $l$ 于点 $P$ ，求弦 $C P$ 的最大值．

查看解析
5、如图1，在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + 1 (k \neq 0)$ 的图像与反比例函数 $y = \frac{6}{x}$ 的图像交于点A、B，与 $y$ 轴交于点C，点A的横坐标为2．

(1)、求 $k$ 的值；

(2)、利用图像直接写出 $k x + 1 < \frac{6}{x}$ 时 $x$ 的取值范围；

(3)、如图2，将直线 $A B$ 沿 $y$ 轴向下平移4个单位，与函数 $y = \frac{6}{x} (x > 0)$ 的图像交于点D，与 $y$ 轴交于点E，再将函数 $y = \frac{6}{x} (x > 0)$ 的图像沿 $A B$ 平移，使点A、D分别平移到点C、F处，求图中阴影部分的面积．

查看解析
6、中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献．为满足新能源汽车的充电需求，某小区增设了充电站，如图是矩形 $P Q M N$ 充电站的平面示意图，矩形 $A B C D$ 是其中一个停车位．经测量， $∠ A B Q = 60 °$ ， $A B = 5.4 m$ ， $C E = 1.6 m$ ， $G H ⊥ C D$ ， $G H$ 是另一个车位的宽，所有车位的长宽相同，按图示并列划定．

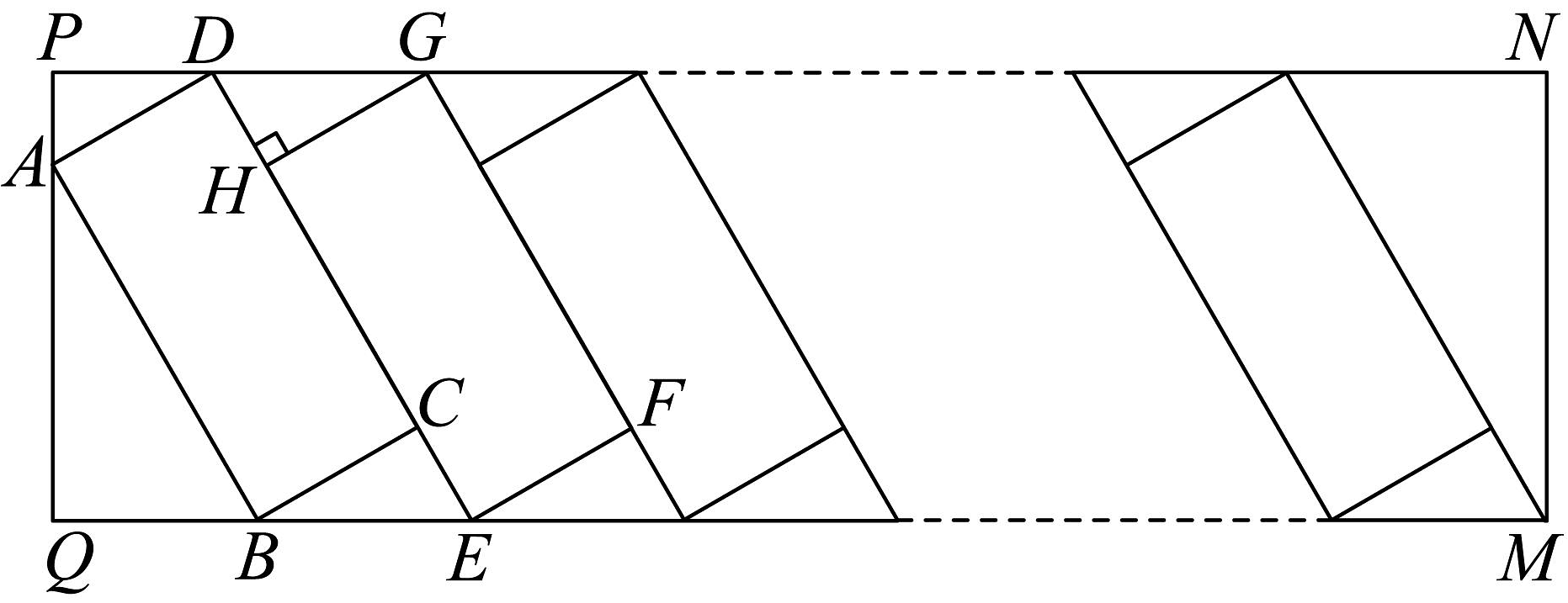
根据以上信息回答下列问题：（结果精确到 $0 .1m$ ，参考数据 $\sqrt{3} \approx 1.73$ ）

(1)、求 $P Q$ 的长；

(2)、该充电站有20个停车位，求 $P N$ 的长．

查看解析
7、如图，在平行四边形 $A B C D$ 中，点 $F$ 在边 $A D$ 上， $A B = A F$ ，连接 $B F$ ，点 $O$ 为 $B F$ 的中点， $A O$ 的延长线交边 $B C$ 于点 $E$ ，连接 $E F$

(1)、求证：四边形 $A B E F$ 是菱形：

(2)、若平行四边形 $A B C D$ 的周长为 $22, C E = 1, ∠ B A D = 120 °$ ，求 $A E$ 的长．

查看解析
8、（1）计算： $\sqrt{4} + |- 4 \cos 60 °| - {(π - 5)}^{0} + {(\frac{1}{2})}^{- 2}$ ；
（2）先化简： $(a + 1 - \frac{3}{a - 1}) \div \frac{a^{2} + 4 a + 4}{a - 1}$ ，再从 $- 2$ ， $0$ ， $1$ ， $2$ 中选取一个适合的数代入求值．

查看解析
9、如图，在矩形 $A B C D$ 中， $B C = \sqrt{2} A B$ ， O为 $B C$ 中点， $O E = A B = 4$ ，则扇形 $E O F$ 的面积为．

查看解析
10、如图1，在平面直角坐标系中，点 $A 、 C$ 分别在 $y$ 轴和 $x$ 轴上， $A B ∥ x$ 轴， $cos B = \frac{4}{5}$ ，点 $P$ 从 $B$ 点出发，以 $1 cm / s$ 的速度沿边 $B A$ 匀速运动，点 $Q$ 从点 $A$ 出发，沿线段 $A O - O C - C B$ 匀速运动．点 $P$ 与点 $Q$ 同时出发，其中一点到达终点，另一点也随之停止运动．设点 $P$ 运动的时间为 $t (s) ， △ B P Q$ 的面积为 $S ({cm}^{2})$ ，已知 $S$ 与 $t$ 之间的函数关系如图2中的曲线段 $O E$ 、线段 $E F$ 与曲线段 $F G$ ．下列说法中正确的个数有（）个．
①点 $Q$ 的运动速度为 $3 cm / s$ ；
②点 $B$ 的坐标为 $(9, 18)$ ；
③线段 $E F$ 段的函数解析式为 $S = \frac{9 t}{2} (3 \leq t \leq 5)$ ；
④曲线 $F G$ 段的函数解析式为 $S = - \frac{9}{10} t^{2} + 9 t (5 \leq t \leq 10)$ ；
⑤若 $△ B P Q$ 的面积是四边形 $O A B C$ 的面积的 $\frac{1}{9}$ ，则时间 $t = 2 \sqrt{2}$ ．
⑥当 $Q$ 在线段 $A O$ 上运动时，存在某一时刻，使得 $△ C Q P$ 周长最小．

A、3 B、4 C、5 D、6

查看解析
11、如图，菱形 $A B C D$ 中， $∠ B =60 °$ ，点 $E$ 是 $A B$ 边上的点， $A E = 4$ ， $B E = 8$ ，点 $F$ 是 $B C$ 上的一点， $△ E G F$ 是以点 $G$ 为直角顶点， $∠ E F G$ 为 $30 °$ 角的直角三角形，连结 $A G$ ．当点 $F$ 在直线 $B C$ 上运动时，线段 $A G$ 的最小值是（）

A、2 B、 $4 \sqrt{3} - 2$ C、 $2 \sqrt{3}$ D、4

查看解析
12、矩形 $O B A C$ 在平面直角坐标系中的位置如图所示，反比例函数 $y = \frac{k}{x}$ 的图象与 $A B$ 边交于点D，与 $A C$ 边交于点F，与 $O A$ 交于点E， $O E = 2 A E$ ，若四边形 $O D A F$ 的面积为2，则k的值是（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{8}{5}$

查看解析
13、烷烃是一类由碳、氢元素组成的有机化合物质，下图是这类物质前四种化合物的分子结构模型图，其中中间的大球代表碳原子，周围的小球代表氢原子．第 $1$ 种如图①有 $4$ 个氢原子，第 $2$ 种如图②有 $6$ 个氢原子，第 $3$ 种如图③有 $8$ 个氢原子，……按照这一规律，第 $1012$ 种化合物的分子结构模型中氢原子的个数是（）

A、 $1013$ B、 $2024$ C、 $2025$ D、 $2026$

查看解析
14、下列计算正确的是（）

A、 $2 a^{3} \cdot a^{2} = 2 a^{6}$ B、 ${(- 2 a)}^{3} \div b \times \frac{1}{b} = - 8 a^{3}$ C、 $(a^{3} + a^{2} + a) \div a = a^{2} + a$ D、 $3 a^{- 2} = \frac{3}{a^{2}}$

查看解析
15、在“五一”期间，我市某旅游景区接待游客103200人次，将103200用科学记数法表示为（）

A、 $1.032 \times 10^{3}$ B、 $1.032 \times 10^{4}$ C、 $1.032 \times 10^{5}$ D、 $1.032 \times 10^{6}$

查看解析
16、探究与拓展
如图1，在平面直角坐标系中，二次函数 $y = - \frac{1}{2} x^{2} + b x + 6$ 的图象与x轴交于A，B两点，与y轴交于点C，点B的坐标为 $(6, 0)$ ，点D是此函数图象在x轴上方部分的动点，连接CD，OD．设点D的横坐标为n， $△ O C D$ 的面积为S，S关于n的函数图象如图2所示．

(1)、请直接写出点A的坐标，b和图2中c的值；

(2)、当 $S = \frac{3}{2}$ 时，求点D的坐标；

(3)、当点D仅在函数图象上点C至点B之间的部分运动时，连接BC，交OD于点E，则 $\frac{O D}{O E}$ 是否存在最大值？若存在，请求出这个最大值并直接写出此时S的值；若不存在，请说明理由．

查看解析
17、综合与实践
【问题情境】如图1，贴窗花是我国特有的喜庆文化之一，我们可以从寓意团圆平安的窗花图案中抽象出一个由两个同心圆构成的几何图形（共同的圆心称为中心），如图2，我们称这种图形为“环花”．
【实践探究】设直线l与“环花”从左到右依次交于点A，B，C，D．
（1）如图2，当直线l经过中心O时，请直接写出线段 $A B$ 与 $C D$ 的数量关系；
（2）如图3，当直线l不经过中心O时，请证明（1）中的结论仍然成立；
【问题深化】（3）如图4，当把“环花”中的两个圆形换成两个相似的菱形时（中心点O是这两个菱形对角线的公共交点， $A B ∥ E F$ 且F，B，D，H四点均在对角线 $F H$ 上），类似地形成了“方花”，直线l不经中心O时，与“方花”从左到右依次交于点M，N，P，Q，求 $\frac{M N}{P Q}$ 的值．

查看解析
18、人工智能+（简称为“ $AI$ ”）已成为推动全球创新和经济增长的重要力量，某校为了培养能够适应未来社会的创新人才，拟开设“ $AI$ 交互设计”、“AI工程实践”、“AI综合技能”、“ $AI$ 创新挑战”、“ $AI$ 轨迹普及”五项“ $AI +$ ”社团课程．为了了解学生对上述五项社团课程的兴趣情况，学校随机抽取部分学生进行问卷调查，并将调查结果绘制成如下所示的条形统计图和扇形统计图（均不完整）．

请根据统计图提供的信息，解答下列问题：

(1)、请将条形统计图补充完整．

(2)、求在扇形统计图中“ $AI$ 轨迹普及”的百分比和表示“ $AI$ 创新挑战”的扇形的圆心角的度数．

(3)、学校对有意向参加“ $AI$ 创新挑战”社团课程的学生进行了现场测试（满分100分），并将成绩统计如下：
成绩/分
83
87
90
92
95
97
人数
2
4
6
8
3
1
则这组数据的平均数是90.5，中位数是______，众数是______．

(4)、若该校学生的总人数是3000人，请你估计有意向参加“AI创新挑战”社团课程的学生有多少人？

查看解析

19、项目式学习

背景

我国是水资源最为紧缺的国家之一，然而在日常生活中，水龙头漏水造成水资源浪费现象仍较为突出．某校园内有一个漏水的水龙头，数学活动小组要探究其漏水造成的浪费情况．同学们用一个带有刻度的量筒放在水龙头下面接水，探究量筒中的总水量 $y$ （毫升）是否为时间 $t$ （分钟）的函数？

素材

每隔1分钟记录量筒中的总水量，但因操作延误，开始计时时量筒中已有少量水，因而得到如下表的一组数据：

时间 $t$ （分钟）	1	2	3	4	5	…
总水量 $y$ （毫升）	10	15	20	25	30	…

问题探究和问题解决

任务1

请在下图的平面直角坐标系内描出上表每对数据所对应的点．

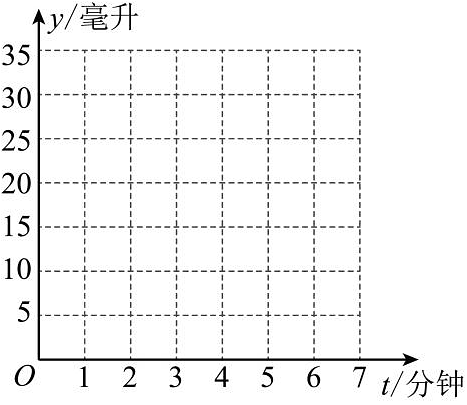
任务2

请根据上表中的数据和所描的点，判断 $y = \frac{k}{t}$ 和 $y = k t + b$ （ $k$ 、 $b$ 为常数）哪一个能正确反映总水量 $y$ 与时间 $t$ 的函数关系？请求出这个关系式．

任务3

①同学们继续观察，当量筒中的水刚好有65毫升时，所需时间是多少分钟？

②照这个漏水速度，请预测此水龙头1小时会浪费多少毫升水？

③请你根据以上的探索和结论，提一条关于水龙头节水管理方面的建议．

查看解析

20、在某次物理实验中，楠楠将一个试验小物件静止地放在斜面 $A B$ 上，其受力情况分析如图所示，重力G的方向竖直向下，其方向线交 $A B$ 于点E，交水平面 $A M$ 于点D，支持力F的方向垂直于 $A B$ ，摩擦力P的方向线与 $A B$ 平行，已知斜面的坡角 $α = 25 °$ ．

(1)、求摩擦力P的方向与重力G的方向的夹角 $β$ 的度数；

(2)、若在此次实验中， $A E = 30 cm$ ， $C E = 2.4 cm$ ，求小物件的铅垂高 $C D$ （结果取整数）．
（参考数据： $\sin 25 ° \approx 0.42$ ， $\cos 25 ° \approx 0.91$ ， $\tan 25 ° \approx 0.47$ ）

查看解析

上一页 1016 1017 1018 1019 1020 下一页跳转

成绩/分	83	87	90	92	95	97
人数	2	4	6	8	3	1