-
1、下列计算正确的是( )A、 B、 C、 D、
-
2、据国家统计局消息:2024年出生人口人,为7年来首次同比增长,数据用科学记数法表示为( )A、 B、 C、 D、
-
3、如果表示零上20度,则零下20度表示( )A、 B、 C、 D、
-
4、以线段、为底,在平面内构造等腰与等腰 , , , , , 且 .
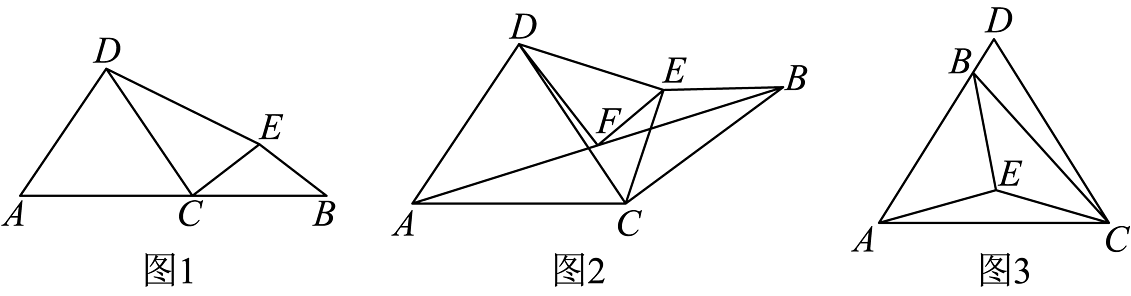 (1)、如图1,当点、、三点共线时,求证:(2)、如图2,当点、、三点不共线时,若 , 连接 , 点为中点,连接、 , 求证:;(3)、如图3,当点在线段上运动且点在直线的下方时(点与、不重合),请直接写出与的数量关系.
(1)、如图1,当点、、三点共线时,求证:(2)、如图2,当点、、三点不共线时,若 , 连接 , 点为中点,连接、 , 求证:;(3)、如图3,当点在线段上运动且点在直线的下方时(点与、不重合),请直接写出与的数量关系. -
5、如图,二次函数的图象与轴交于、两点,与轴交于点 , 一次函数经过点、、 . 点是直线上方二次函数图象上的一个动点,过点作直线轴于点 , 交直线于点 , 连接 .
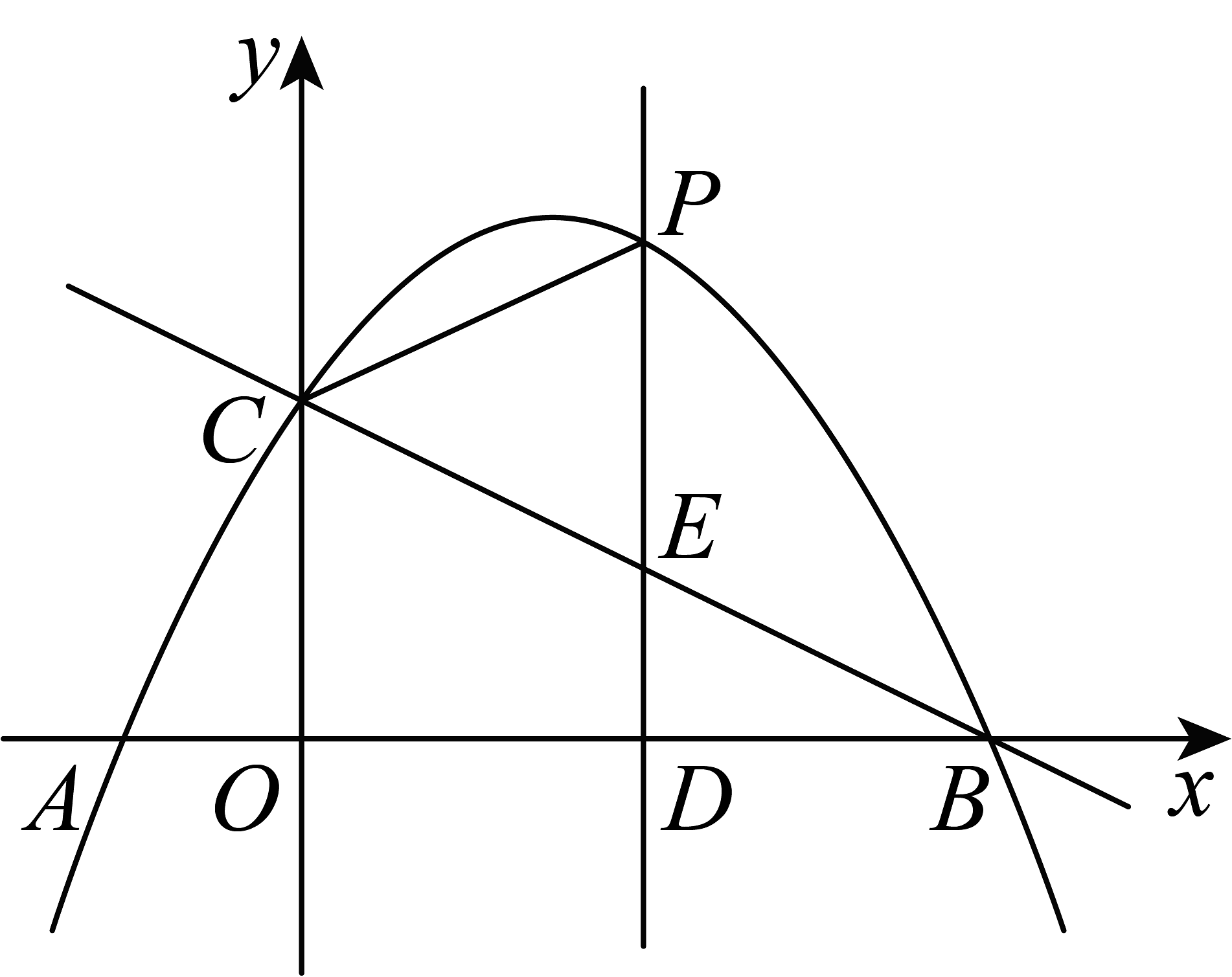 (1)、求二次函数和一次函数的解析式;(2)、当是以为底边的等腰三角形时,求点的坐标;(3)、连接 , 连接交于点 , 记面积为 , 面积为 , 在点运动的过程中,判断是否存在最大值,若存在,求出其最大值,若不存在,请说明理由.
(1)、求二次函数和一次函数的解析式;(2)、当是以为底边的等腰三角形时,求点的坐标;(3)、连接 , 连接交于点 , 记面积为 , 面积为 , 在点运动的过程中,判断是否存在最大值,若存在,求出其最大值,若不存在,请说明理由. -
6、已知点在以为直径的圆上,过点、作圆的切线,交于点 , 连 ,
 (1)、证明:;(2)、若 , 求的值.
(1)、证明:;(2)、若 , 求的值. -
7、几位同学在老师的指导下,利用课余时间进行测量活动.
活动主题
篮球架的结构
测量工具
皮尺、测角仪、计算器等
活动过程
模型抽象
篮球架(如实物图所示)的结构示意图如下:立柱垂直地面 , 横梁平行地面 , 篮筐与横梁在同一直线上,点、、在同一条垂直于地面的直线上.
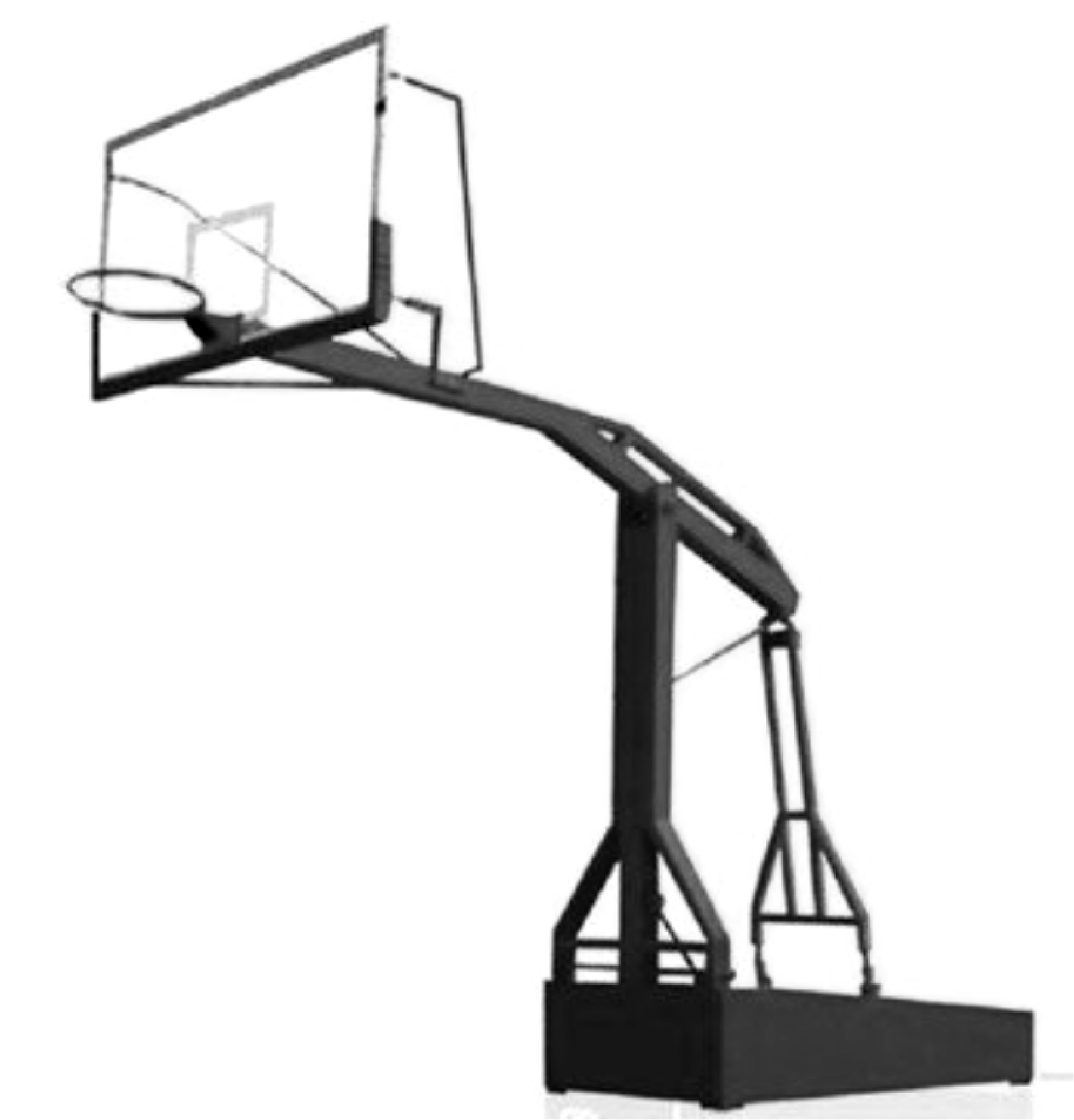

测绘过程与数据信息
①用测角仪在处测得后拉杆与水平面的夹角 , 在处测得伸臂与水平面的夹角;
②用皮尺测得后拉杆的长为 , 伸臂的长为 , 箱体的高度为;
③用计算器计算得到: , , , , , .
请根据表格中提供的信息,解决下列问题(结果精确到)
(1)、求立柱的高度;(2)、已知墩墩站立时手臂举至最高处,手掌距地面最大高度为 , 若墩墩站在地面上想摸到篮筐 , 则墩墩至少跳多高才能摸到篮筐? -
8、2025年1月20日,DeepSeek发布了其最新的推理大模型,又一次引起人们对人工智能的关注,人工智能是数字经济高质量发展的引擎.人工智能基于功能和应用领域可分为以下几类::决策类人工智能;:人工智能机器人;:语音类人工智能;:视觉类人工智能.某公司就“你最关注的人工智能类型”对员工进行了一次调查,并将调查结果绘制成下面两幅不完整的统计图.
 (1)、①此次共调查了________人;
(1)、①此次共调查了________人;②扇形统计图(图2)中类对应的圆心角度数为________ .
③请将条形统计图(图1)补充完整.
(2)、将表示四个类型的字母 , , , 依次写在四张卡片上,卡片背面完全相同,将四张卡片背面朝上洗匀放置在平面上,从中随机抽取一张,记录卡片内容后放回洗匀,再随机抽取一张,请用列表或画树状图的方法,求抽取到的两张卡片内容不一致的概率. -
9、已知关于的一元二次方程有两个相等的实根,(1)、求的值.(2)、求代数式的值.
-
10、下面是小明设计的“作菱形”的尺规作图过程.
求作:菱形 .
作法:①作线段;②作线段的垂直平分线 , 交于点;③在直线上取点 , 以为圆心,长为半径画弧,交直线于点(点与点不重合);④连接、、、 . 所以四边形为所求作的菱形.
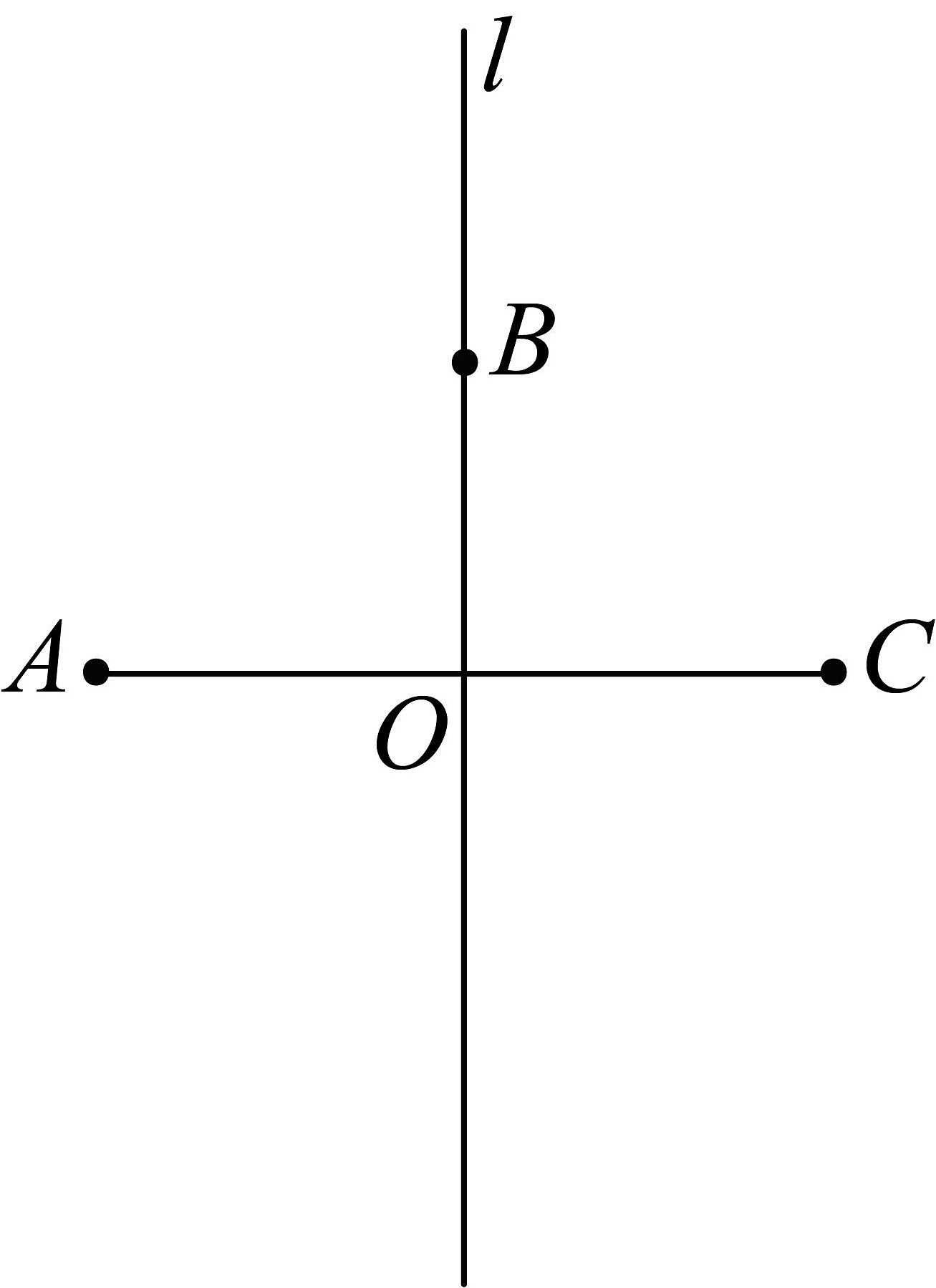
根据小明设计的尺规作图过程,完成下列任务:
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、证明:四边形为菱形. -
11、解方程 .
-
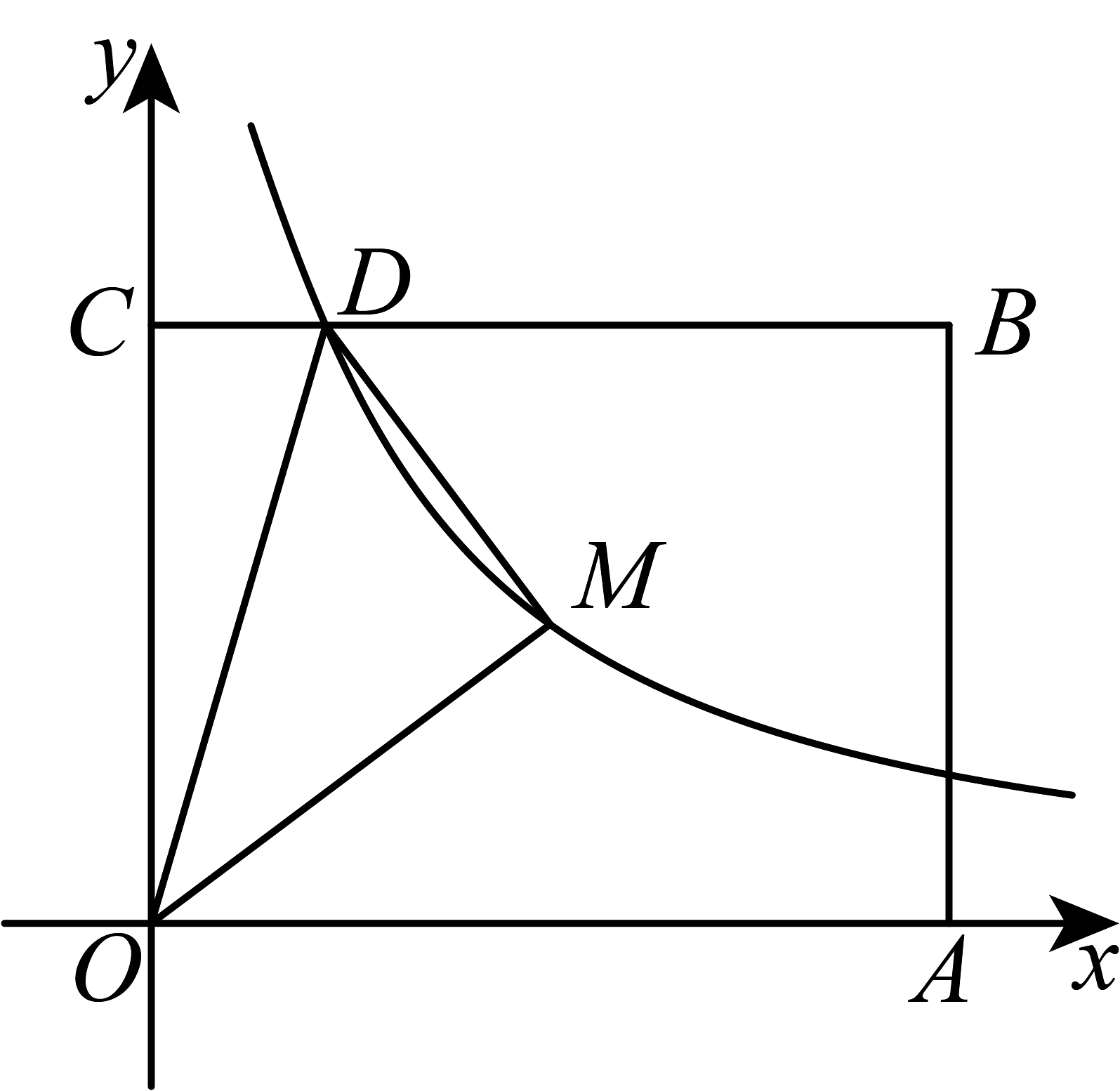
12、如图,矩形的顶点 , 分别在轴,轴的正半轴上.反比例函数的图象过矩形的对称中心 , 交于点 . 现给出以下结论:
①;
②的面积为;
③点 , 可能关于直线对称;
④若平分 , 则
其中正确的是 . (写出所有正确结论的序号)
-
13、若a为方程的解,则的值为 .
-
14、如图,平行四边形的对角线相交于点 , 若 , 则这个平行四边形的面积为 .

-
15、如图,已知a∥b,直角三角板的直角顶点在直线a上,若∠1=30°,则∠2= .

-
16、小红拿出一张正方形的纸片,在上面剪出一个扇形和一个圆,尝试后发现圆恰好是该圆锥的底面,(圆心与圆锥顶点同在如图虚线上)测量后得知,圆锥母线长 , 则以下这张正方形纸片的边长是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、如图,拱桥可以近似地看作直径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为150m,那么这些钢索中最长的一根的长度为( )
 A、50m B、40m C、30m D、25m
A、50m B、40m C、30m D、25m -
18、如图,二次函数y=ax2+bx+c与反比例函数y=的图象相交于点A(﹣1,y1)、B(1,y2)、C(3,y3)三个点,则不等式ax2+bx+c>的解集是( )
 A、﹣1<x<0或1<x<3 B、x<﹣1或1<x<3 C、﹣1<x<0或x>3 D、﹣1<x<0或0<x<1
A、﹣1<x<0或1<x<3 B、x<﹣1或1<x<3 C、﹣1<x<0或x>3 D、﹣1<x<0或0<x<1 -
19、如图,是中国秦初至清末部分朝代历经的时间.下列说法正确的是( )
 A、明朝时间最长 B、隋朝时间最短 C、有4个朝代超过250年 D、若西汉,东汉合并为汉,则汉朝时间最长
A、明朝时间最长 B、隋朝时间最短 C、有4个朝代超过250年 D、若西汉,东汉合并为汉,则汉朝时间最长 -
20、某校开展“运用几何画板,探寻美丽的数学世界”活动,下面是活动的部分作品,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、