-
1、
综合与实践
【问题情境】如图1,贴窗花是我国特有的喜庆文化之一,我们可以从寓意团圆平安的窗花图案中抽象出一个由两个同心圆构成的几何图形(共同的圆心称为中心),如图2,我们称这种图形为“环花”.
【实践探究】设直线与“环花”从左到右依次交于点 , , , .
(1)如图2,当直线经过中心时,请直接写出线段与的数量关系;
(2)如图3,当直线不经过中心时,请证明(1)中的结论仍然成立;
【问题深化】
(3)如图4,当把“环花”中的两个圆形换成两个相似的菱形时(中心点是这两个菱形对角线的公共交点,且 , , , 四点均在对角线上),类似地形成了“方花”,直线不经中心时,与“方花”从左到右依次交于点 , , , , 求的值.

-
2、随着人工智能技术的快速发展,AI+已成为推动全球创新和经济增长的重要力量.某校为了培养能够适应未来社会的创新人才,拟开设“AI交互设计”“AI工程实践”“AI综合技能”“AI创新挑战”“AI轨迹普及”五项人工智能社团课程.为了解学生对上述五项社团课程的兴趣情况,随机抽取部分学生进行问卷调查(调查问卷如图所示),并将调查结果绘制成如下所示的条形统计图和扇形统计图(均不完整).

请根据统计图提供的信息,解答下列问题.
(1)、请将条形统计图补充完整.(2)、在扇形统计图中,“AI轨迹普及”的百分比是 , 表示“AI创新挑战”的扇形的圆心角度数为 度.(3)、学校对有意向参加“AI创新挑战”社团课程的学生进行了现场测试(满分100分),并将成绩统计如下:成绩/分
83
87
90
92
95
97
人数
2
4
6
8
3
1
则这组数据的平均数是 分,中位数是 分,众数是 分.
(4)、若该校学生的总人数是1200人,请你估计最有意向参加“AI创新挑战”社团课程的学生有多少人? -
3、在某次物理实验中,楠楠将一个试验小物件静止地放在斜面上,其受力情况分析如图所示,重力的方向竖直向下,其方向线交于点 , 交水平面于点 , 支持力的方向垂直于 , 摩擦力的方向线与平行,已知斜面的坡角 .
 (1)、求摩擦力的方向与重力的方向的夹角的度数;(2)、若在此次实验中, , , 求小物件的铅垂高(结果取整数).
(1)、求摩擦力的方向与重力的方向的夹角的度数;(2)、若在此次实验中, , , 求小物件的铅垂高(结果取整数).(参考数据: , , )
-
4、如图,在平面直角坐标系中,每个正方形小方格的边长都是一个单位长度,的三个顶点 , , 均在格点上.
 (1)、将向下平移4个单位长度,请你画出平移后得到的;(2)、将绕点顺时针旋转后得到的 , 请你画出;(3)、在(2)的条件下,求点运动路径的长.
(1)、将向下平移4个单位长度,请你画出平移后得到的;(2)、将绕点顺时针旋转后得到的 , 请你画出;(3)、在(2)的条件下,求点运动路径的长. -
5、(1)计算:;
(2)解不等式组:
-
6、如图,在中, , , , 点是边的中点,点是上的动点,连接 , 将沿翻折得到 , 连接 , 则的最小值为 .

-
7、如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于点和 . 则关于方程的解是( )
 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 , -
8、下列计算正确的是( )A、 B、 C、 D、
-
9、如图,是的直径,若 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、已知关于的一元二次方程:有两个不相等的实数根,则的取值范围是( )A、 B、 C、 D、
-
11、如图,已知直线 , 被直线所截,则的同位角是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、下列交通指示标志的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
13、下列图形是平面图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
14、如图,抛物线与轴相交于 , 两点(点在点的左侧),其中 , 是方程的两个根,抛物线与轴相交于点 .
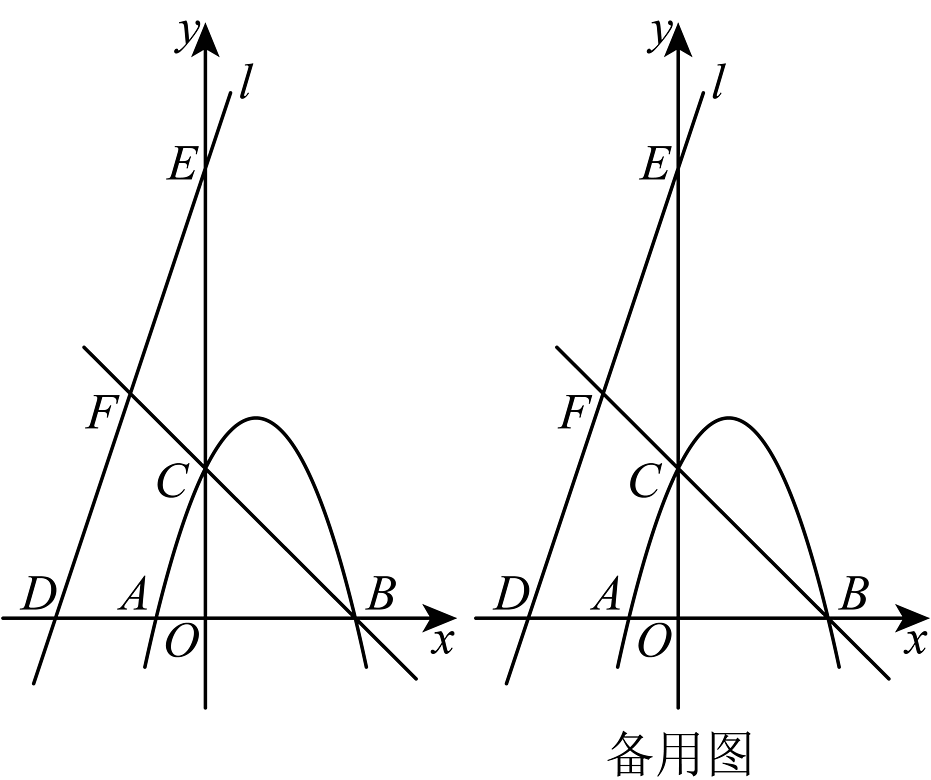 (1)、求该抛物线对应的函数表达式;(2)、已知直线与 , 轴分别相交于点 , .
(1)、求该抛物线对应的函数表达式;(2)、已知直线与 , 轴分别相交于点 , .①设直线与相交于点 , 问在第三象限内的抛物线上是否存在点 , 使得?若存在,求出点的坐标;若不存在,说明理由;
②过抛物线上一点作直线的平行线.与抛物线相交于另一点 . 设直线 , 相交于点 . 连接 , . 求线段的最小值.
-
15、化简分式: , 并求值(请从小宇和小丽的对话中确定 , 的值)
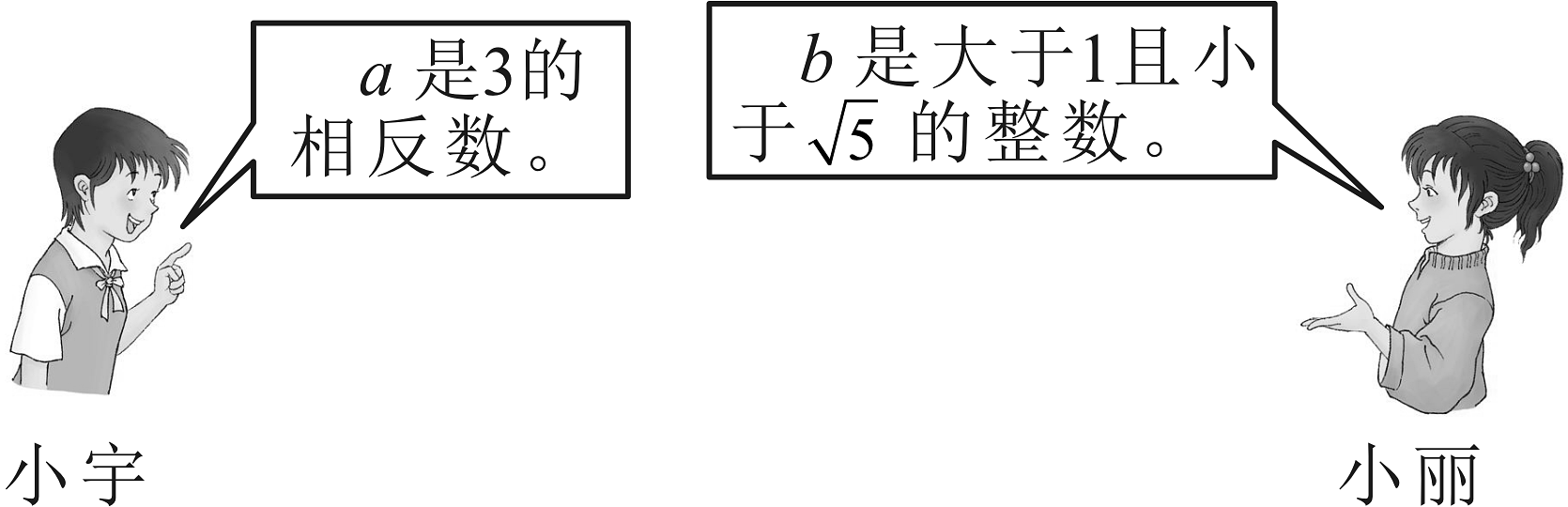
-
16、如图,已知 , 点 , 在线段上,且 .
请从①;②;③中.选择一个合适的选项作为已知条件,使得 .
你添加的条件是:__________(只填写一个序号).
添加条件后,请证明 .

-
17、如图,在平面直角坐标系中,作直线与轴相交于点 , 与抛物线相交于点 , 连接 , 相交于点 , 得和 , 若将其面积之比记为 , 则 .

-
18、计算: .
-
19、某日,甲、乙两人相约在一条笔直的健身道路上锻炼.两人都从地匀速出发,甲健步走向地.途中偶遇一位朋友,驻足交流后,继续以原速步行前进;乙因故比甲晚出发 , 跑步到达地后立刻以原速返回,在返回途中与甲第二次相遇.下图表示甲、乙两人之间的距离与甲出发的时间之间的函数关系.( )

那么以下结论:
①甲、乙两人第一次相遇时,乙的锻炼用时为;
②甲出发时,甲、乙两人之间的距离达到最大值;
③甲、乙两人第二次相遇的时间是在甲出发后;
④ , 两地之间的距离是 .
其中正确的结论有:
A、①②③ B、①②④ C、①③④ D、②③④ -
20、数学兴趣小组成员小刚对自己的学习质量进行了测试.如图是他最近五次测试成绩(满分为100分)的折线统计图,那么其平均数和方差分别是( )
 A、95分, B、96分, C、95分,10 D、96分,10
A、95分, B、96分, C、95分,10 D、96分,10