-
1、小芳要用硬纸片制作一个几何体,如图是该几何体的展开图.
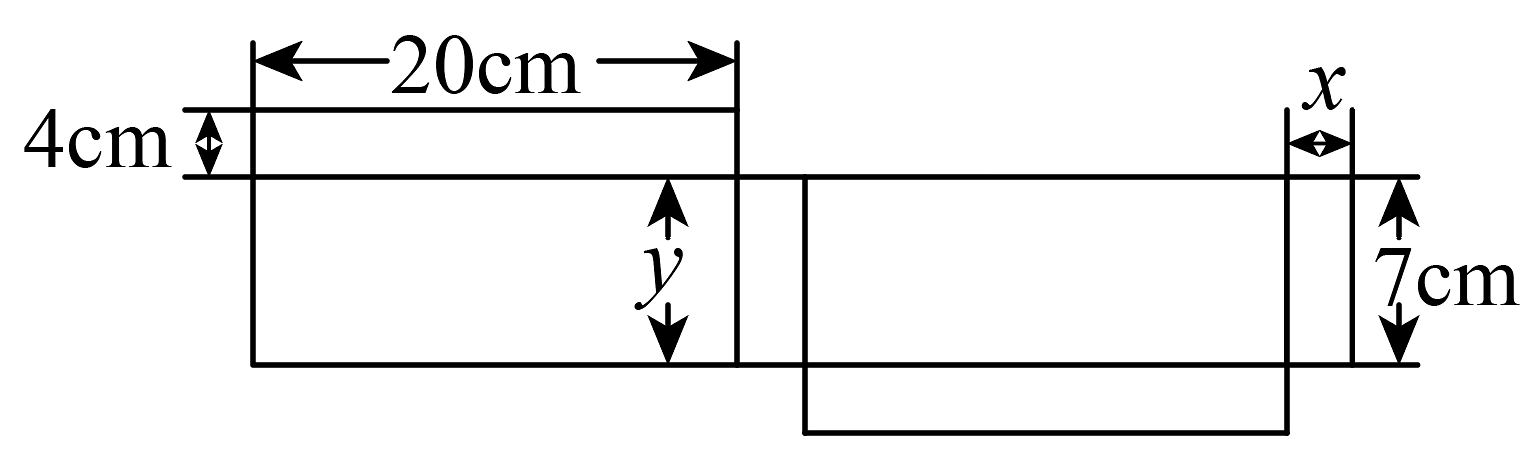 (1)、该几何体为 ;(2)、图中 , ;(3)、求几何体的体积.
(1)、该几何体为 ;(2)、图中 , ;(3)、求几何体的体积. -
2、下面四个整式中,不能表示图中阴影部分面积的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、已知二次函数(a为常数).
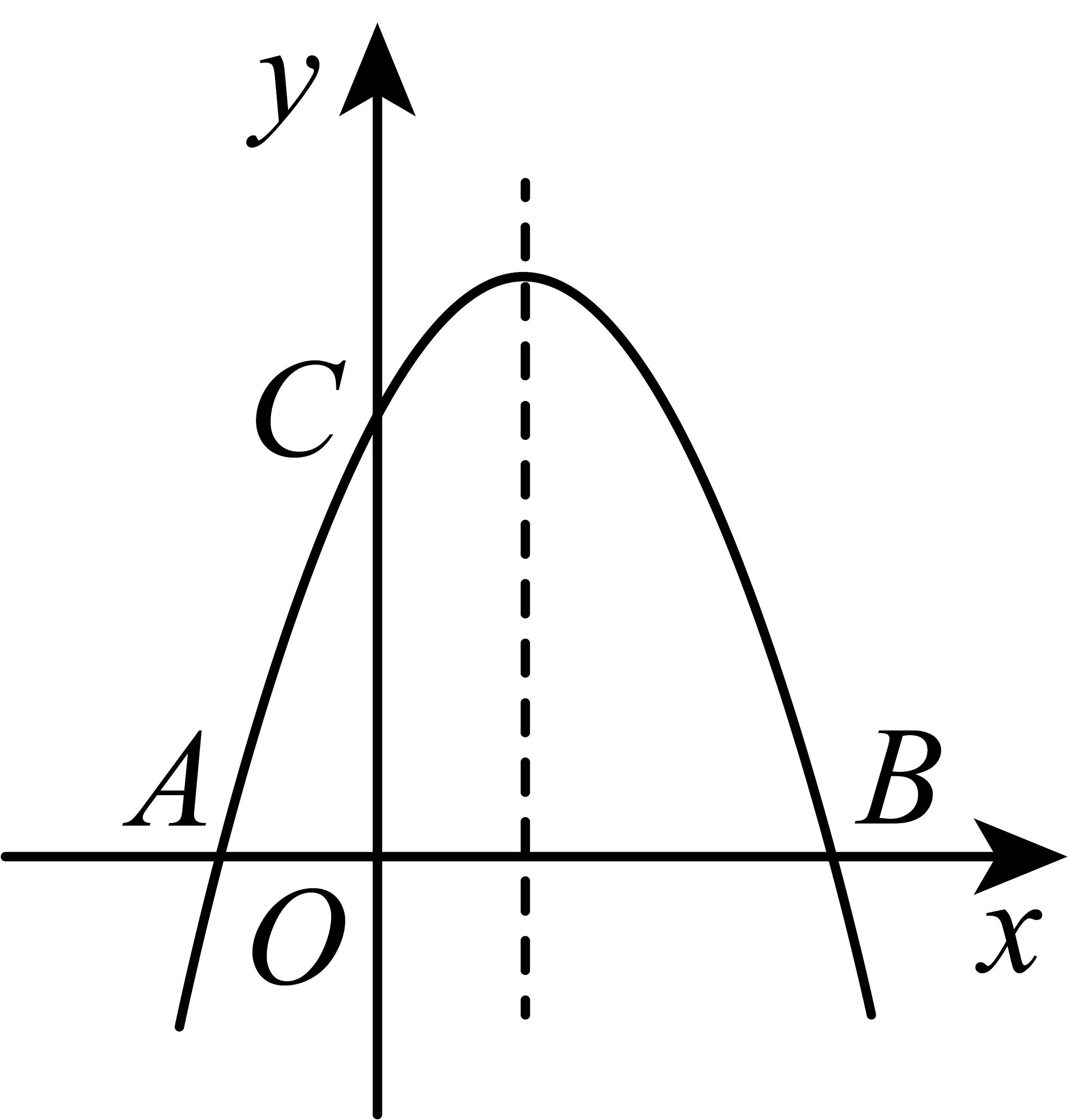 (1)、求证:不论a为何值,该二次函数图象与x轴总有两个公共点;(2)、当时,该二次函数的最大值与最小值之差为9,求此时函数的解析式;(3)、若二次函数图象对称轴为直线 , 该函数图象与x轴交于两点(点A在点B左侧),与y轴交于点C.点C关于对称轴的对称点为D,点M为的中点,过点M的直线l(直线l不过两点)与二次函数图象交于两点,直线与直线相交于点P.
(1)、求证:不论a为何值,该二次函数图象与x轴总有两个公共点;(2)、当时,该二次函数的最大值与最小值之差为9,求此时函数的解析式;(3)、若二次函数图象对称轴为直线 , 该函数图象与x轴交于两点(点A在点B左侧),与y轴交于点C.点C关于对称轴的对称点为D,点M为的中点,过点M的直线l(直线l不过两点)与二次函数图象交于两点,直线与直线相交于点P.①求证:点P在一条定直线上;
②若 , 请直接写出满足条件的直线l的解析式,不必说明理由.
-
4、【问题背景】2024年4月23日是第18个“世界读书日”,为给师生提供更加良好的阅读环境,学校决定扩大图书馆面积,增加藏书数量,现需购进20个书架用于摆放书籍.
【素材呈现】
素材一:有两种书架可供选择,A种书架的单价比B种书架单价高;
素材二:用18000元购买A种书架的数量比用9000元购买B种书架的数量多6个;
素材三:A种书架数量不少于B种书架数量的 .
【问题解决】
(1)、问题一:求出两种书架的单价;(2)、问题二:设购买a个A种书架,购买总费用为w元,求w与a的函数关系式,并求出费用最少时的购买方案;(3)、问题三:实际购买时,商家调整了书架价格,A种书架每个降价m元,B种书架每个涨价元,按问题二的购买方案需花费21120元,求m的值. -
5、(1)解不等式组
(2)先化简,再求值: , 其中x满足 .
-
6、已知一次函数和 , 当时,函数的图象在函数的图象上方,则a的取值范围为
-
7、如图,在菱形中, , 点O是对角线的中点,以点O为圆心,长为半径作圆心角为的扇形 , 点D在扇形内,则图中阴影部分的面积为( )
 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定 -
8、如图1,菱形的边在平面直角坐标系中的轴上,点 , 点是菱形的边的中点,反比例函数经过点 .
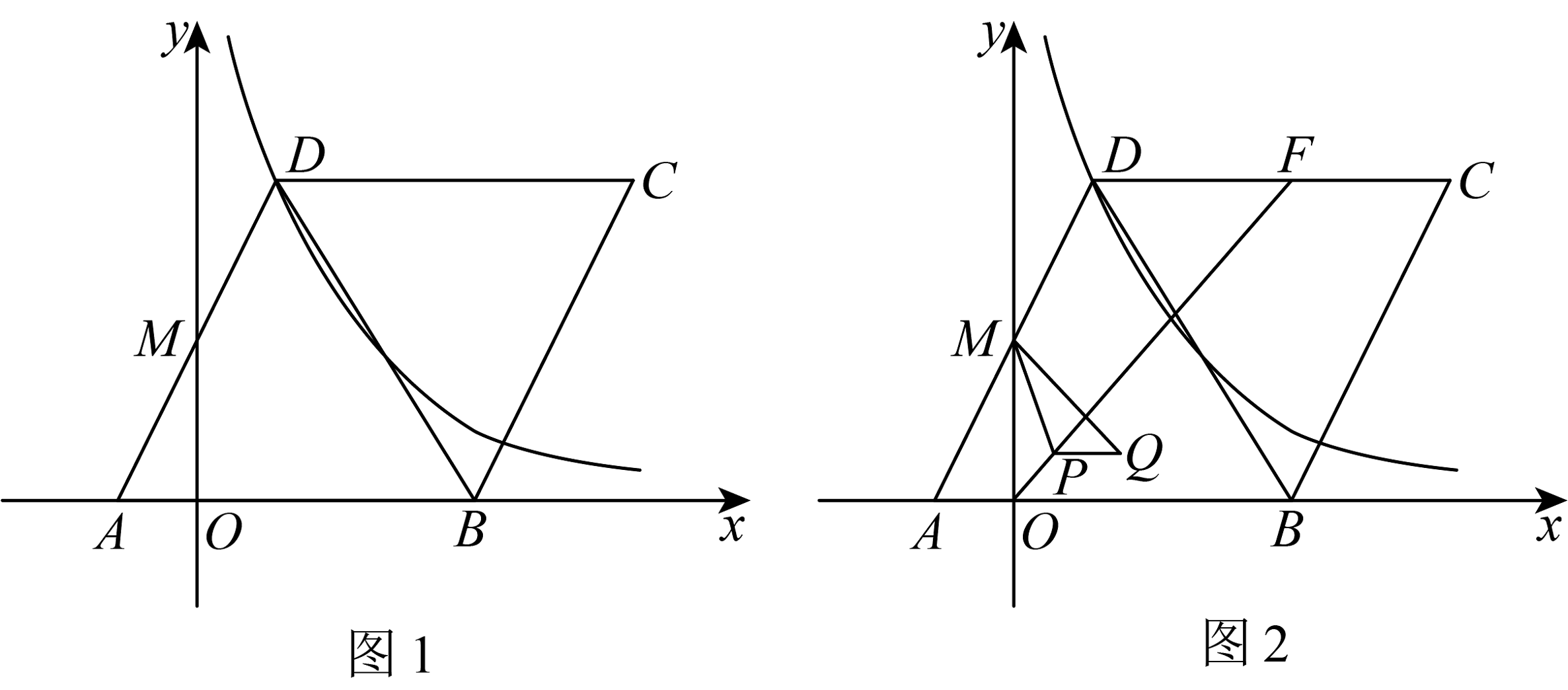 (1)、求反比例函数的表达式;(2)、点为图像上的一动点,过点做轴于点 , 若点使得和相似,求点的坐标;(3)、如图2,点在上,连接 , , 点是线段上的动点,连接 , 作关于直线的轴对称图形 , 作的外接圆 , 当的圆心在菱形上或内部时,求的半径的取值范围.
(1)、求反比例函数的表达式;(2)、点为图像上的一动点,过点做轴于点 , 若点使得和相似,求点的坐标;(3)、如图2,点在上,连接 , , 点是线段上的动点,连接 , 作关于直线的轴对称图形 , 作的外接圆 , 当的圆心在菱形上或内部时,求的半径的取值范围. -
9、如图,在矩形中, , , 连接 , 将绕点顺时针方向旋转,与能够重合在一起,连接 , .
 (1)、求的值;(2)、在绕点旋转过程中,当点落在对角线上时,求的长;(3)、连接 , 试探究能否构成以为直角边的 , 若能,直接写出线段的长;若不能,请说明理由.
(1)、求的值;(2)、在绕点旋转过程中,当点落在对角线上时,求的长;(3)、连接 , 试探究能否构成以为直角边的 , 若能,直接写出线段的长;若不能,请说明理由. -
10、综合与实践
【主题】鲜艳的中华人民共和国国旗始终是当代中华儿女永不褪色的信仰,国旗上的每颗星都是标准五角星,为了增强学生的国家荣誉感、民族自豪感等,数学王老师组织学生对五角星进行了较深入的研究,其中智慧数学小组发现国旗上五角星的五个角都是顶角为36°的等腰三角形,对此三角形产生了极大的兴趣并展开探究.

【探究发现】如图1,在中, , .
(1)操作发现:将折叠,使边落在边上,点的对应点是点 , 折痕交于点 , 连接DE,DB,设 , , 求的值(用含的式子表示);
(2)进一步探究发现,顶角的等腰三角形的底与腰的比值为 , 这个比值被称为黄金比,请在(1)的条件下证明:
【拓展应用】(3)当等腰三角形的底与腰的比等于黄金比时,这个三角形叫做黄金三角形.例如,图1中的是黄金三角形.如图2,在菱形中, , , 请直接写出这个菱形较长的对角线长.
-
11、端午节是我国的传统节日,粽子是端午节的一种美食,寓意幸福安康.某商店在端午节来临之前,购进咸肉粽子和豆沙粽子两种进行销售,已知每个咸肉粽子的进价是每个豆沙粽子进价的2倍,用1600元购进咸肉粽子的数量比用700元购进豆沙粽子的数量多50个.(1)、求咸肉粽子和豆沙粽子每个进价分别为多少元?(2)、若某商店把咸肉粽子以6元/每个销售,那么半个月可以售出200个.根据销售经验,把咸肉粽子的单价每提高2元,销量会相应减少40个.将售价定为多少元时,才能使半个月获得的利润最大?最大利润是多少?
-
12、如图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(是基座的高,是主臂,是伸展臂,).已知基座高度为 , 主臂长为5m,测得主臂伸展角 . (参考数据: , , , ).
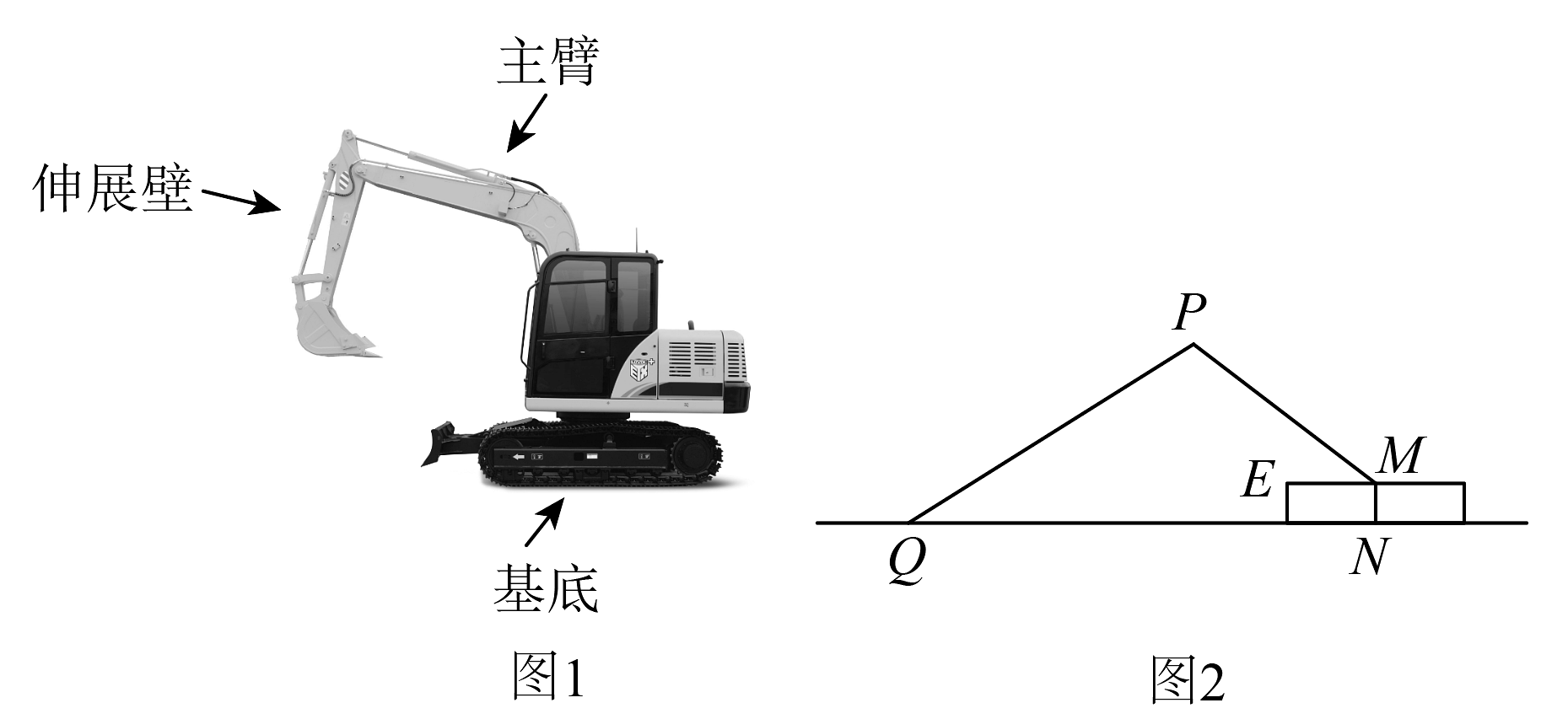 (1)、求点到地面的高度;(2)、当挖掘机挖到地面上的点时, , 求的度数.
(1)、求点到地面的高度;(2)、当挖掘机挖到地面上的点时, , 求的度数. -
13、计算:
-
14、已知点在一次函数的图象上,则 .
-
15、某班开展“强国有我”主题演讲,共有2位男同学和3位女同学报名参加,现从中随机抽取1位同学进行演讲,则抽到男同学的概率为 .
-
16、因式分解: .
-
17、已知点 , , 都在二次函数的图象上,则 , , 的大小关系为( )A、 B、 C、 D、
-
18、不等式组的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、
-
19、若关于的一元二次方程有实数根,则的取值范围为( )A、 B、 C、 D、
-
20、已知,点和关于原点中心对称,则( )A、 B、 C、 D、