-
1、如图,在小山的东侧A点有一个热气球,受西风的影响,以的速度沿与地面成角的方向飞行,后到达点C处,此时热气球上的人测得小山西侧B点的俯角为 , 则小山东西两侧A,B两点间的距离为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图,是的一条弦,直径于点 . 若 , , 则的直径为( )
 A、5 B、6 C、 D、13
A、5 B、6 C、 D、13 -
3、关于x的方程有实数根,则k的取值范围是( )A、且 B、 C、 D、
-
4、已知二次函数 , 将其函数图象向右平移1个单位长度,再向下平移1个单位长度得到的抛物线所对应的解析式应是( )A、 B、 C、 D、
-
5、以下说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , , 则
-
6、随着中国“一带一路”朋友圈的不断扩大,对外贸易持续快速增加,截至2024年底中欧班列(成渝)累计开行超36000列,将36000用科学记数法表示应是( )A、 B、 C、 D、
-
7、下列几何体中,主视图是三角形的几何体是( )A、
 B、
B、 C、
C、 D、
D、
-
8、下列图标中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
9、2的算术平方根是( )A、 B、 C、4 D、
-
10、如图,在▱中, , , , 为边上的动点.连接 , 将绕点逆时针旋转得到 , 过点作 , 交直线于点 . 连接、 , 分别取、的中点、 , 连接 , 交于点 .
 (1)、若点与点重合,则线段的长度为______.(2)、随着点的运动,与的长度是否发生变化?若不变,求出与的长度;若改变,请说明理由.
(1)、若点与点重合,则线段的长度为______.(2)、随着点的运动,与的长度是否发生变化?若不变,求出与的长度;若改变,请说明理由. -
11、在中,点在边上,若 , 则称点是点的“关联点”.
 (1)、如图(1),在中,若 , 于点 . 试说明:点是点的“关联点”.(2)、如图(2),已知点在线段上,用无刻度的直尺和圆规作一个 , 使其同时满足下列条件:①点为点的“关联点”;②是钝角(保留作图痕迹,不写作法).(3)、若为锐角三角形,且点为点的“关联点”.设 , , 用含、的代数式表示的取值范围(直接写出结果).
(1)、如图(1),在中,若 , 于点 . 试说明:点是点的“关联点”.(2)、如图(2),已知点在线段上,用无刻度的直尺和圆规作一个 , 使其同时满足下列条件:①点为点的“关联点”;②是钝角(保留作图痕迹,不写作法).(3)、若为锐角三角形,且点为点的“关联点”.设 , , 用含、的代数式表示的取值范围(直接写出结果). -
12、如图,在徐州云龙湖旅游景区,点为“彭城风华”观演场地,点为“水族展览馆”,点为“徐州汉画像石艺术馆”.已知 , , . 求“彭城风华”观演场地与“水族展览馆”之间的距离(精确到).(参考数据: , )

-
13、参加初中学业水平考试的人数简称“中考人数”.如图,某市根据2016﹣2024年中考人数及2024年上半年小学、初中各年级在校学生人数,绘制出2016﹣2032年中考人数(含预估)统计图如图:
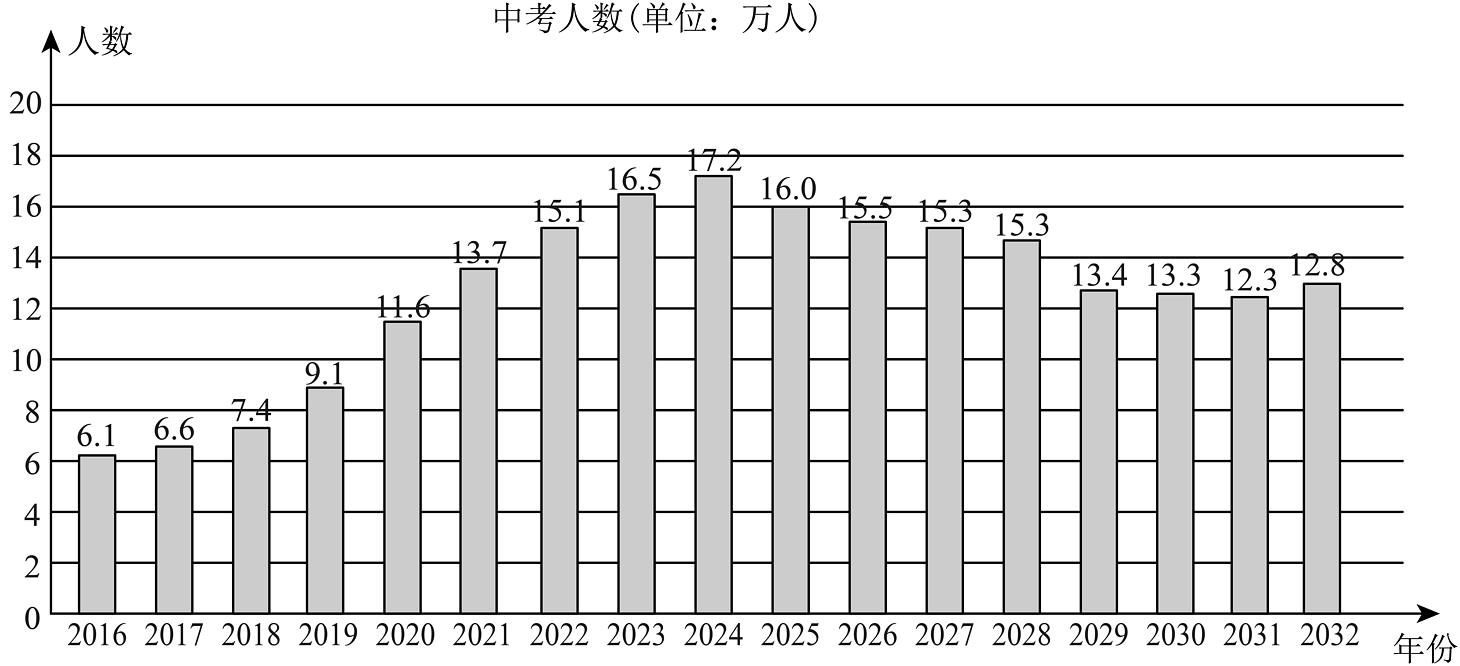
根据以上信息,解决下列问题.
(1)、下列结论中,所有正确结论的序号是______.①2016﹣2031年中考人数呈现先升后降的趋势;
②与上一年相比,中考人数增加最多的年份是2021年;
③2016﹣2024年中考人数的波动比2024﹣2032年中考人数的波动大.
(2)、为促进人口长期均衡发展,有效提高人口出生率,我国于2013﹣2021年先后实施了三项鼓励生育的政策,其中导致该市2032年中考人数较2031年增加的最主要原因是______.A.2013年单独两孩政策
B.2015年全面两孩政策
C.2021年三孩生育政策
(3)、2024年上半年,该市小学在校学生共有多少人? -
14、中国古代数学著作《张邱建算经》中有一道问题;“今有甲、乙怀钱,各不知其数.甲得乙十钱,多乙余钱五倍.乙得甲十钱,适等.问甲、乙怀钱各几何?”问题大意:甲、乙两人各有钱币若干枚.若乙给甲10枚钱,此时甲的钱币数比乙的钱币数多出5倍,即甲的钱币数是乙钱币数的6倍;若甲给乙10枚钱,此时两人的钱币数相等.问甲、乙原来各有多少枚钱币?请用二元一次方程组解答上述问题.
-
15、不透明的袋子中装有2个红球与2个白球,这些球除颜色外无其他差别.(1)、甲从袋子中随机摸出1个球,摸到红球的概率为______;(2)、甲、乙两人分别从袋子中随机摸出1个球(不放回),用列表或画树状图的方法,求两人摸到相同颜色球的概率.
-
16、计算:(1)、;(2)、 .
-
17、将圆锥的侧面沿一条母线剪开后展平,所得扇形的面积为 , 圆心角θ为 , 圆锥的底面圆的半径为 .
-
18、如图,是的直径,点在的延长线上,与相切于点 , 若 , 则°.

-
19、小明的速度与时间的函数关系如图所示,下列情境与之较为相符的是( )
 A、小明坐在门口,然后跑去看邻居家的小狗,随后坐着逗小狗玩 B、小明攀岩至高处,然后顺着杆子滑下来,随后躺在沙地上休息 C、小明跑去接电话,然后坐下来电话聊天,随后步行至另一个房间 D、小明步行去朋友家,敲门发现朋友不在家,随后步行回家
A、小明坐在门口,然后跑去看邻居家的小狗,随后坐着逗小狗玩 B、小明攀岩至高处,然后顺着杆子滑下来,随后躺在沙地上休息 C、小明跑去接电话,然后坐下来电话聊天,随后步行至另一个房间 D、小明步行去朋友家,敲门发现朋友不在家,随后步行回家 -
20、一次函数与二次函数的图象如图所示,则不等式的解集为( )
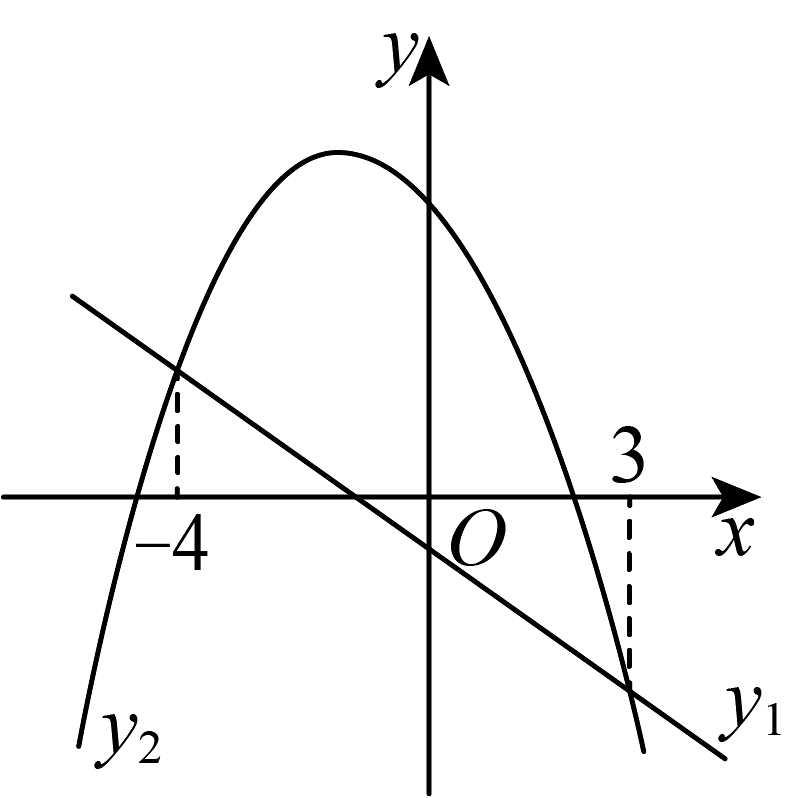 A、 B、 C、 D、或
A、 B、 C、 D、或