-
1、已知：如图，四边形 ， E为边上一点．
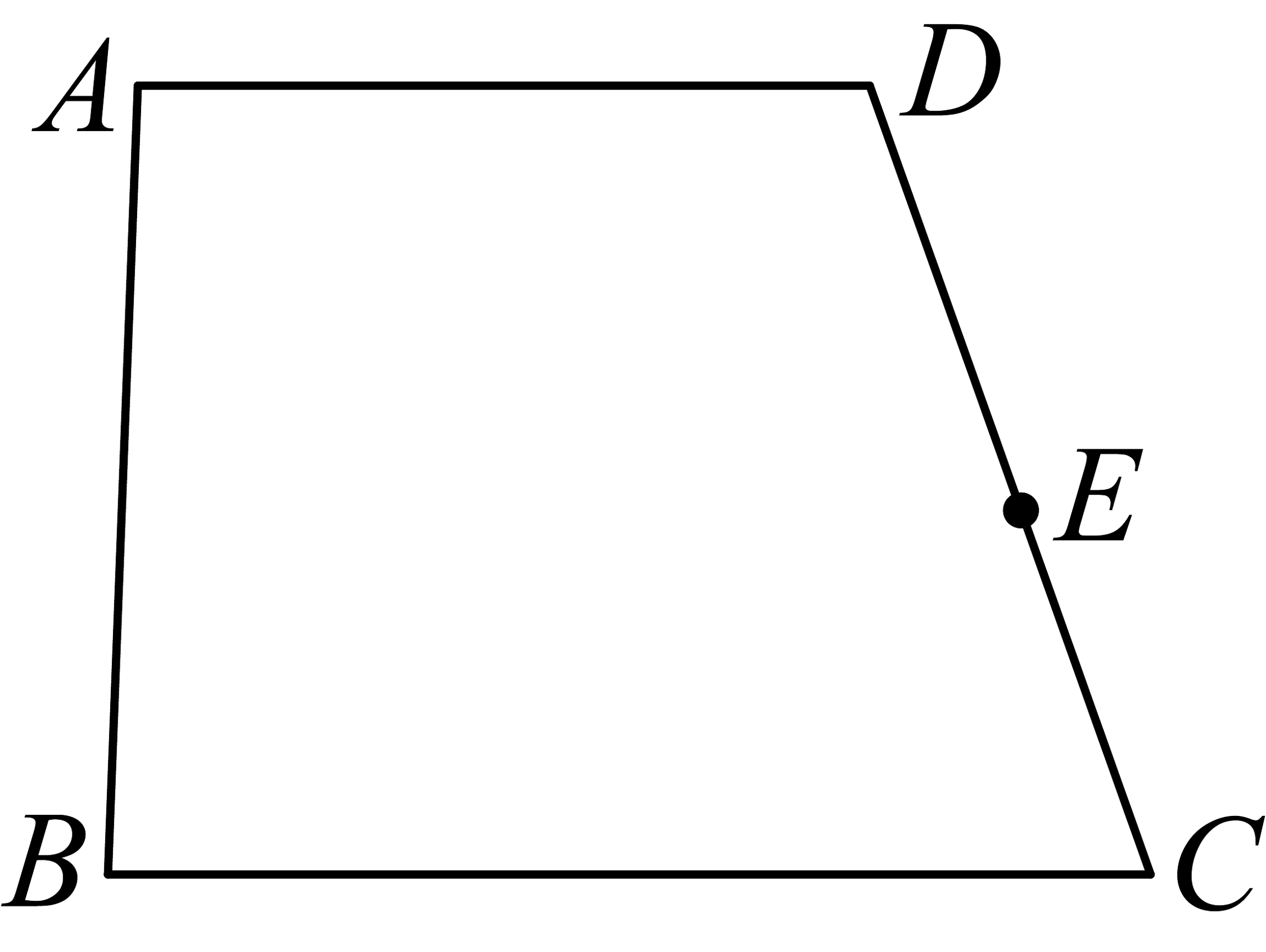
求作：四边形内一点P，使 ， 且点P到的距离相等．
-
2、如图①，将边长为的正方形纸板沿虚线剪掉边长为的小正方形，得到如图②的“纸板卡”，若用这样完全相同的“纸板卡”拼成正方形，最少需要块；如图③，将长、宽、高分别为的长方体砖块，切割掉长、宽、高分别为的长方体，得到如图④的“直角砖块”，若用这样完全相同的“直角砖块”拼成正方体，最少需要块．
-
3、计算： ．
-
4、下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
-
5、如图，四边形内接于 ， 若 ， ， 则的半径是（ ）
A、 B、 C、 D、4 -
6、如图是“垃圾入桶”标志及垃圾桶的平面示意图，若 ， ， 则的度数是（ ）
A、 B、 C、 D、 -
7、如图1，AB是⊙O的直径，弦CD交AB于点E，连结OC，AC，且∠AOC=2∠ACE.
(1)、求证：AB⊥CD；(2)、如图2，点F是上一点， ， 连结AF分别交CD，BD于点G，H，①若点H恰好是BD的中点，求证：BD=AC；
②若DE=DH，求sin∠B的值.
-
8、已知二次函数y=-x2+bx+c的图象的对称轴是直线x=1，并经过点(3，0).(1)、求二次函数表达式；(2)、将函数图象向上平移m（m>0）个单位长度，图象与x轴相交于点A，B(点A在点B的左侧)，当BO=2AO时，求m的值；(3)、若n>0，当n≤x≤n+1时，二次函数的最大值是2n，求n的值.
-
9、甲、乙两车从A地驶向B地，并以各自的速度匀速行驶甲车比乙车提早2h出发，并且甲车途中休息了1h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象.
(1)、求出图中a= ， m=.(2)、求出甲车行驶路程y（km）与时间x（h)的函数表达式，并写出相应x的取值范围；(3)、当乙车行驶多长时间时，两车恰好相距30km. -
10、如图，在Rt△ABC中，CD是斜边AB上的中线.
(1)、延长线段AC，请用无刻度的直尺和圆规在射线AC上找一点E，使∠CBE=∠BCD（保留作图痕迹，不写作法)：(2)、若AC=6，BC=8，求BE的长. -
11、为了激发学生对人工智能的兴趣，普及人工智能知识，某初中学校组织七、八年级学生参加入工智能科普测试，为了了解活动效果，从两个年级中各抽取10名学生的成绩进行整理分析，分成A，B，C，D四组（用x表示成绩分数)，A组：90≤x≤100，B组：80≤x<90，C组：70≤x<80，D组：x<70，下面是部分信息：
七年级10人的得分：48，57，69，72，84，84，86，91，92，96：
八年级10人的得分在B组中的分数为：84，85，85，86；
两组数据的平均数、中位数、众数如下表所示：
年级
平均数
中位数
众数
七
77.8
84
a
八
77.8
b 85
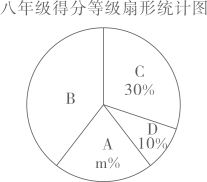
根据以上信息，解答下列问题：
(1)、填空：a= ， b= ， m=.(2)、如果该校七年级有1000人参加测试，八年级有800人参加测试，请估计七、八两个年级得分在A组的共有多少人？(3)、根据以上数据，你认为哪个年级在此次人工智能科普测试中表现更好，请说明理由。 -
12、如图，在等腰中， ， ， 过点B作于点D.
(1)、求AD的长：(2)、若点E是BC中点，连结AE，求tan∠EAC的值. -
13、先化简，再求值： ， 其中.
-
14、计算：
-
15、如图，在矩形ABCD中，连结BD，点E是线段BD上一动点，连结AE，点B关于直线AE的对称点为点F，当点F落在边CD上时，DF=4CF，连结AF交BD于点G，若S△GEF=20，则矩形ABCD的面积为.
-
16、如图，在△ABC中，∠ACB=30°，将△ABC绕点C顺时针旋转80°得到△DEC，点A，B的对应点分别为D，E，延长DE恰好经过点A，则∠B的度数为.
-
17、用半径为6的半圆形纸片围成一个圆锥侧面，则这个圆锥的底面半径为.
-
18、一枚质地均匀的骰子每个面上分别标着数字1，2，3，4，5，6.任意抛掷这枚骰子一次，朝上一面出现的数是奇数的概率是.
-
19、若分式的值为0，则x的值为.
-
20、如图①的图案称“赵爽弦图”，是我国汉代数学家赵爽在注解《周髀算经》时给出的，它由四个全等的直角三角形围成一个大正方形，中间是个小正方形，我们在此图形中连结四条线段得到如图②的图案，记阴影部分的面积为 ， 空白部分的面积为 ， 若 ， 则大正方形的边长与小正方形的边长的比值为（ ）
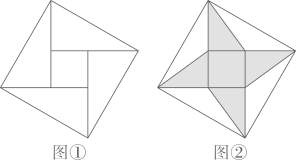A、 B、 C、 D、2