-
1、如图,在中, , , , 点D在BC边上,且 , , 垂足为E,连结CE
 (1)、求的值.(2)、求的度数.
(1)、求的值.(2)、求的度数. -
2、先化简,再求值: , 其中.
-
3、计算:.
-
4、如图,在菱形ABCD中, , , E是AB边上的一点, , 将四边形AEFD沿着EF折叠得到四边形A'D'FE,当三点A',B,D'在同一条直线上时,°,此时D'F交BC边于点G,CG的长为.

-
5、如图,在平面直角坐标系中,点A(0,4),B(3,4),将向右平移一定距离,得到 , 点F为DE中点,函数的图像经过点C和点F,则k的值是.

-
6、动车组列车的普通坐席位置通常用A,B,C,D,F五个字母表示,其中A,F代表靠窗坐席,小红随机购买了一张动车组列车的普通坐席车票,坐席是靠窗位置的概率为.
-
7、方程组的解为.
-
8、因式分解:a2-6a=.
-
9、如图,在正方形ABCD中,将边AB绕点A逆时针旋转至AF,使F点落在正方形ABCD内部,延长BF交的平分线于点H,连结FD交AH于点G,则下列比值是定值的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、点 , , 在反比例函数的图象上,且 , 则下列判断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
11、如图,在中,分别以这个三角形的三边为边长向外侧作正方形,其面积分别记为 , , .若 , 则图中阴影部分的面积为( )
 A、6 B、 C、5 D、
A、6 B、 C、5 D、 -
12、小鹿两次购买相同药物的费用均为200元,第二次购买时每盒降价8元,他多买了2盒.设第一次购买时该药品的单价为x(元/盒),则可列方程为( )A、 B、 C、 D、
-
13、如图,与位似,位似中心为点O,OC':OC=3:4,的面积为9,则面积为( )
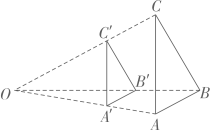 A、12 B、 C、16 D、18
A、12 B、 C、16 D、18 -
14、下列计算正确的是( )A、 B、 C、 D、
-
15、已知扇形的半径为6,圆心角为 , 则它的面积是( )A、 B、 C、 D、
-
16、据文化旅游部数据显示,2024年国庆节假期,全国国内出游约1467000000人次,将1467000000个数用科学记数法表示为( )A、 B、 C、 D、
-
17、如图,该几何体的俯视图是( )
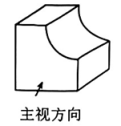 A、
A、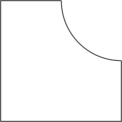 B、
B、 C、
C、 D、
D、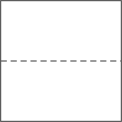
-
18、-2025的绝对值为( )A、2025 B、-2025 C、 D、
-
19、 如图,在矩形中,过A作于点H , 交于点E , 以为直径作与相交于点F , 连接并延长交于点G , 连接并延长交射线于点P .
 (1)、求证:是等腰三角形;(2)、如图1,与相交于点Q , 若点Q为的中点,求的值;(3)、如图2,已知 , , 求的长.
(1)、求证:是等腰三角形;(2)、如图1,与相交于点Q , 若点Q为的中点,求的值;(3)、如图2,已知 , , 求的长. -
20、 在平面直角坐标系中,抛物线 .
 (1)、若 , 抛物线与x轴只有一个交点.
(1)、若 , 抛物线与x轴只有一个交点.①求证:;
②抛物线的顶点为A , 与y轴相交于点B , 直线的表达式为 . 求在范围内,x等于多少时,取得最大值?
(2)、点在该抛物线上, . 若 , 求t的取值范围.