-
1、如图,可用一个正方形制作成一副“七巧板”,利用“七巧板”能拼出各种各样的图案,根据“七巧板”的制作过程,请你解答下列问题.

(1)、“七巧板”的七个图形,可以归纳为三种不同形状的平面图形,即一块正方形,一块和五块.(2)、请按要求将七巧板的七块图形重新拼接(不重叠,并且图形中间不留缝隙),在下面空白处画出示意图.
①拼成一个等腰直角三角形;②拼成一个长与宽不等的长方形;③拼成一个六边形.(3)、发挥你的想象力,用七巧板拼成一个图案,在下面空白处画出示意图,并在图案旁边写出简明的解说词. -
2、如图 (1)、(2)都是几何体的平面展开图,先想一想,再折一折,然后说出图 (1)、(2)折叠后的几何体名称、底面形状、侧面形状、棱数、侧棱数与顶点数.
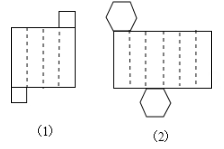
-
3、用一个平面去截一个几何体,截得的多边形可能有哪几种?请把结果画出来.
-
4、用白萝卜等材料做一个正方体,并把正方体表面涂上颜色.
 (1)、把正方体的棱二等分,然后沿等分线把正方体切开,得到8个小正方体.观察其中三面被涂色的有a个,如图①,那么a等于;(2)、把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体.观察其中三面被涂色的有a个,各面都没有涂色的b个,如图②,那么a+b=;(3)、把正方体的棱四等分,然后沿等分线把正方体切开,得到64个小正方体.观察其中两面被涂成红色有c个,各面都没有涂色的b个,如图③,那么b+c=.
(1)、把正方体的棱二等分,然后沿等分线把正方体切开,得到8个小正方体.观察其中三面被涂色的有a个,如图①,那么a等于;(2)、把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体.观察其中三面被涂色的有a个,各面都没有涂色的b个,如图②,那么a+b=;(3)、把正方体的棱四等分,然后沿等分线把正方体切开,得到64个小正方体.观察其中两面被涂成红色有c个,各面都没有涂色的b个,如图③,那么b+c=. -
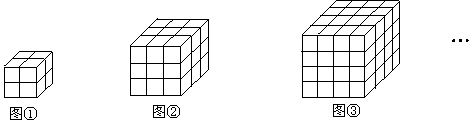
5、如图所示,是一个由小立方块搭成的几何体的俯视图,小正方体中的数字表示在该位置的小立方块的个数,试画出它的主视图与左视图.
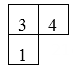
-
6、请画出下列几何体的主视图、左视图、俯视图.

-
7、 一只蚂蚁从如图所示的正方体的一顶点A沿着棱爬向B,只能经过三条棱,共有种走法.

-
8、如图是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于1的正方形.问这个直三棱柱的体积是.
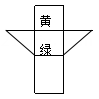
-
9、 立方体木块的六个面分别标有数字1、2、3、4、5、6,下图是从不同方向观察这个立方体木块看到的数字情况,数字1和5对面的数字的和是.
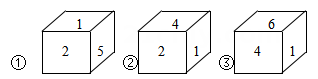
-
10、 图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是.

-
11、 下面4个图形均由6个相同的小正方形组成,折叠能围成一个正方体的是.
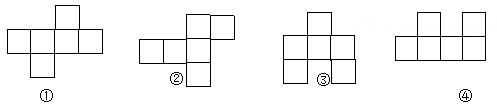
-
12、如左下图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为.
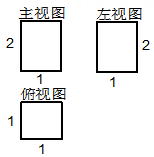
-
13、展览厅内要用相同的正方体木块搭成一个三视图如图所示的展台,则此展台共需这样的正方体块.

-
14、如图所示是一个立体图形的展开图,请写出这个立体图形的名称:.
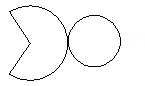
-
15、一个正棱锥有六个顶点,所有侧棱长的和为30cm,则每条侧棱的长是cm.
-
16、 下图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,那么该几何体的主视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
17、 一个几何体是由若干个相同的正方体组成的,其主视图和左视图如图所示,则这个几何体最多可由多少个这样的正方体组成?( )
 A、12个 B、13个 C、14个 D、18个
A、12个 B、13个 C、14个 D、18个 -
18、 如图,用一个平面去截长方体,则截面形状为( )
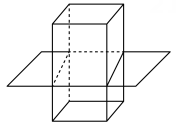 A、
A、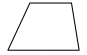 B、
B、 C、
C、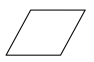 D、
D、
-
19、如图(1)是一个小正方体的侧面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上一面的字是( )
 A、奥 B、运 C、圣 D、火
A、奥 B、运 C、圣 D、火 -
20、如图是一个正四面体,它的四个面都是正三角形,现沿它的三条棱AC、BC、CD剪开展成平面图形,则所得的展开图是( )
 A、
A、 B、
B、 C、
C、 D、
D、