-
1、如图所示的数轴中,点A 表示1,点 B 表示-2,试回答下列问题.
 (1)、A,B 两点之间的距离是.(2)、观察数轴,与点 A 的距离为 5 的点表示的数是.(3)、若将数轴折叠,使点 A 与表示-3的点重合,则点 B 与表示数的点重合.(4)、若数轴上M,N 两点之间的距离为2024(点 M在点 N的左侧),且M,N 两点经过(3)中折叠后互相重合,则M,N 两点表示的数分别是和.
(1)、A,B 两点之间的距离是.(2)、观察数轴,与点 A 的距离为 5 的点表示的数是.(3)、若将数轴折叠,使点 A 与表示-3的点重合,则点 B 与表示数的点重合.(4)、若数轴上M,N 两点之间的距离为2024(点 M在点 N的左侧),且M,N 两点经过(3)中折叠后互相重合,则M,N 两点表示的数分别是和. -
2、一辆校车从学校出发,向东行了3千米,到达小英家,继续向东行了1.54千米,到达小李家,又向西行了9.54千米到达小明家,最后回到学校.(1)、以学校为原点,向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家、小李家、小英家的位置.(2)、小明家距小英家多远?(3)、汽车一共行驶了多少千米?(4)、若汽车的耗油量为0.15 升/千米,则汽车共耗油多少升?
-
3、规定一种新运算:如3. 请计算下列各式的值.(1)、(-3)☆(-5).(2)、(-5)☆[3☆(-2)].
-
4、已知 z是绝对值最小的有理数,求 的值.
-
5、计算.(1)、(2)、(3)、(4)、
-
6、魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.根据刘徽的这种表示法,观察图①,可推算图②中所得的结果为.

-
7、已知某快递公司的收费标准如下:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克2元.圆圆在该快递公司寄一件8千克的物品,需要付费元.
-
8、规定一种新的运算:A★B=A×B-A÷B.如4★2=4×2-4÷2=6,则6★(-3)的值为.
-
9、学习了有理数的加法后,乐乐同学画出了下图进行知识梳理,图中 A 处应填:.
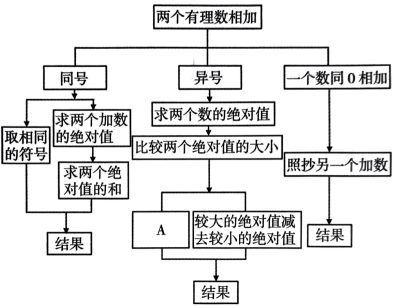
-
10、小明做这样一道题:“计算:|(-3)+■|”,其中“■”表示被墨水污染看不清的一个数,他翻开书后面的答案知该题的计算结果是8,那么“■”表示的数是.
-
11、用科学记数法表示一个数记为 则这个数原来是.
-
12、将一列有理数-1,2,-3,4,-5,6,…按如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(点 C 的位置)是有理数4,那么“峰7”中点 C 的位置是有理数 , 2024应排在A,B,C,D,E 的 位置.其中两个空应依次填写( )
 A、-29,E B、30,A C、-31,D D、34,C
A、-29,E B、30,A C、-31,D D、34,C -
13、如图,数轴上一动点 A 向左移动4个单位长度到达点 B,再向右移动1个单位长度到达点 C,点C表示的数为-1,若将A,B,C 三点表示的数进行混合运算(每个数只能用一次),则可得到的最大数为( )
 A、9 B、8 C、6 D、5
A、9 B、8 C、6 D、5 -
14、下面框中是用手势计算7×8和8×9的示例,且左手伸出的手指数不大于右手伸出的手指数.若用手势计算7×9,左、右手依次伸出手指的根数是( )
 A、2,4 B、1,4 C、3,4 D、3,1
A、2,4 B、1,4 C、3,4 D、3,1 -
15、在实数a、b、c中,若 , 则下列结论:.其中正确的有( )A、1个 B、2个 C、3个 D、4个
-
16、下列计算正确的是( )A、 B、 C、 D、
-
17、下列说法不正确的是( )A、0既不是正数,也不是负数 B、-a 一定是负数 C、任何正数都大于它的相反数 D、绝对值小于3的所有整数的和为0
-
18、下面有理数比较大小正确的是( )A、 B、 C、 D、
-
19、某工程项目总投资约为370000000元,370000000用科学记数法表示是( )A、 B、 C、 D、
-
20、我国是最早采用正负数表示相反意义的量,并进行负数运算的国家.如果向南走3米,记作+3米,那么向北走 6 米,记作( )A、+9米 B、16米 C、-6米 D、-3米