-
1、 在图所示的轴对称图形中,对称轴有2条的图形有( )
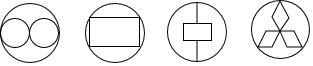 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
2、 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,若AD=2,AB=4,则点D到BC的距离是( )
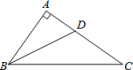 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5 -
3、 交通警察要求司机开车时遵章行驶,在下列交通标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
4、如图,在边长为6 的正方形 ABCD中,E 是边CD 的中点,将 沿AE 折叠至 延长 EF 交 BC 于点G,连接AG,且 AG平分
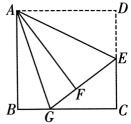 (1)、试说明:(2)、求 BG 的长.
(1)、试说明:(2)、求 BG 的长. -
5、周末,小明和小亮去公园放风筝,为了测得风筝的垂直高度CE,他们进行了如下操作:
①测得水平距离 BD 的长为12米;
②根据手中剩余线的长度计算出风筝线 BC 的长为20米;
③牵线放风筝的小明的身高为1.65米.
 (1)、求风筝的垂直高度CE;(2)、如果小明想风筝沿CD方向下降7 米,则他应该往回收线多少米?
(1)、求风筝的垂直高度CE;(2)、如果小明想风筝沿CD方向下降7 米,则他应该往回收线多少米? -
6、如图,在笔直的公路 AB 旁有一座山,为方便运输货物,现要从公路AB 上的D 处开凿隧道修通一条公路到 C 处,已知点 C 与公路上的停 靠站 A 的距离为15 km,与公路上另一停靠站 B 的距离为 20km,停靠站 A,B之间的距离为25 km,且
 (1)、求修建的公路CD的长;(2)、若公路CD 修通后,一辆货车从 C 处经过点D 到B 处的路程是多少?
(1)、求修建的公路CD的长;(2)、若公路CD 修通后,一辆货车从 C 处经过点D 到B 处的路程是多少? -
7、在等边中,点 D,E 分别在边 BC,AC 上,若∥过点E作交 BC的延长线于点F,求 的值.

-
8、如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16 cm,在容器内壁离容器底部4 cm 的点 B 处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿 4 cm 的点 A 处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm ,则该圆柱底面周长为.

-
9、已知,在 中, , 一只蜗牛从C点出发,以每分钟 20cm 的速度沿 CA→AB→BC的路径爬行再回到C 点,需要的时间是分钟.
-
10、如图所示,OC 为 的平分线, 4,则点 C 到射线OA 的距离为.
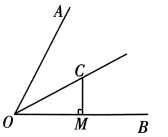
-
11、如图,一根长10米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时AO长8米,当木棒A 端沿墙下滑至点A'时,B端沿地面向右滑行至点. 若 米,则 的长为( )
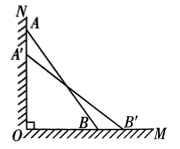 A、1米 B、1.5米 C、3米 D、2米
A、1米 B、1.5米 C、3米 D、2米 -
12、如图是一个外轮廓为长方形的机器零件平面示意图,根据图中的尺寸(单位: mm),计算两圆孔中心 A 和B 的距离为( )
 A、90 mm B、100 mm C、120 mm D、150 mm
A、90 mm B、100 mm C、120 mm D、150 mm -
13、如图所示,点 E 在正方形ABCD 内,满足 6,BE=8,则阴影部分的面积是 ( )
 A、48 B、60 C、76 D、80
A、48 B、60 C、76 D、80 -
14、一棵大树在一次强台风中折断倒下,大树折断前高度估计为18 m,倒下后树顶落在距树根部大约12 m处,这棵大树离地面约几米处折断 ( )
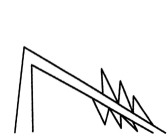 A、3 m B、4 m C、5 m D、6 m
A、3 m B、4 m C、5 m D、6 m -
15、如图是在正方形网格中的△ABC,若小方格边长为1,则△ABC 是 ( )
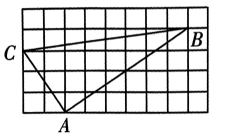 A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对
A、直角三角形 B、锐角三角形 C、钝角三角形 D、以上答案都不对 -
16、已知在△ABC中, 的对边分别是a,b,c.下列条件不能判断△ABC 是直角三角形的是( )A、 B、 C、 D、
-
17、旋转变换在平面几何中有着广泛的应用,特别是在解(证)有关等腰三角形、正三角形、正方形等问题时,更是经常用到的思维方法.请你用旋转变换等知识解决下面的问题.
如图①所示,△ABC与△DCE均为等腰直角三角形,DC与AB交于点M,CE与AB交于点N.
(1)、以点C为中心,将△ACM逆时针旋转90°,画出旋转后的△A'CM';(2)、在(1)的基础上,证明:AM2+BN2=MN2;(3)、如图②所示,在四边形ABCD中,∠BAD=45°,∠BCD=90°,CA平分∠BCD,若BC=4,CD=3,则对角线AC的长度为多少? -
18、如图①所示,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
 (1)、操作发现
(1)、操作发现如图②所示,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是;
②设△BDC的面积为S1 , △AEC的面积为S2 , 则S1与S2的数量关系是.
(2)、猜想论证当△DEC绕点C旋转到图③所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想.
-
19、如图所示,在△ABC中,BC=4 cm,将△ABC以0.2 cm/s的速度沿BC所在直线向右平移,所得图形为△DEF,设运动时间为t s.
 (1)、若∠ADE=60°,求∠B的度数;(2)、当t为何值时,EC=1 cm?
(1)、若∠ADE=60°,求∠B的度数;(2)、当t为何值时,EC=1 cm? -
20、如图所示,在平面直角坐标系中,已知A(-2,-4),B(0,-4),C(1,-1).
 (1)、画出△ABC绕点O逆时针旋转90°后的图形△A1B1C1;(2)、将(1)中所得的△A1B1C1先向左平移4个单位长度,再向上平移2个单位长度得到△A2B2C2 , 画出△A2B2C2;(3)、若△A2B2C2可以看作△ABC绕某点旋转得来,求旋转中心的坐标.
(1)、画出△ABC绕点O逆时针旋转90°后的图形△A1B1C1;(2)、将(1)中所得的△A1B1C1先向左平移4个单位长度,再向上平移2个单位长度得到△A2B2C2 , 画出△A2B2C2;(3)、若△A2B2C2可以看作△ABC绕某点旋转得来,求旋转中心的坐标.