-
1、某市12月上旬每天平均空气质量指数分别为35,42,55,78,57,64,58,69,74,82.为了描述这十天空气质量的变化情况,最适合用的统计图是( )A、折线统计图 B、频数直方图 C、条形统计图 D、扇形统计图
-
2、小红想了解自己打字的速度,应采用收集数据的方式是( )A、查阅资料 B、问卷调查 C、实地调查 D、试验
-
3、在△ABC中,∠ABC=80°,点E在BC边上,D是射线AB上的一个动点,将△BDE沿DE折叠,使点B落在点B'处.
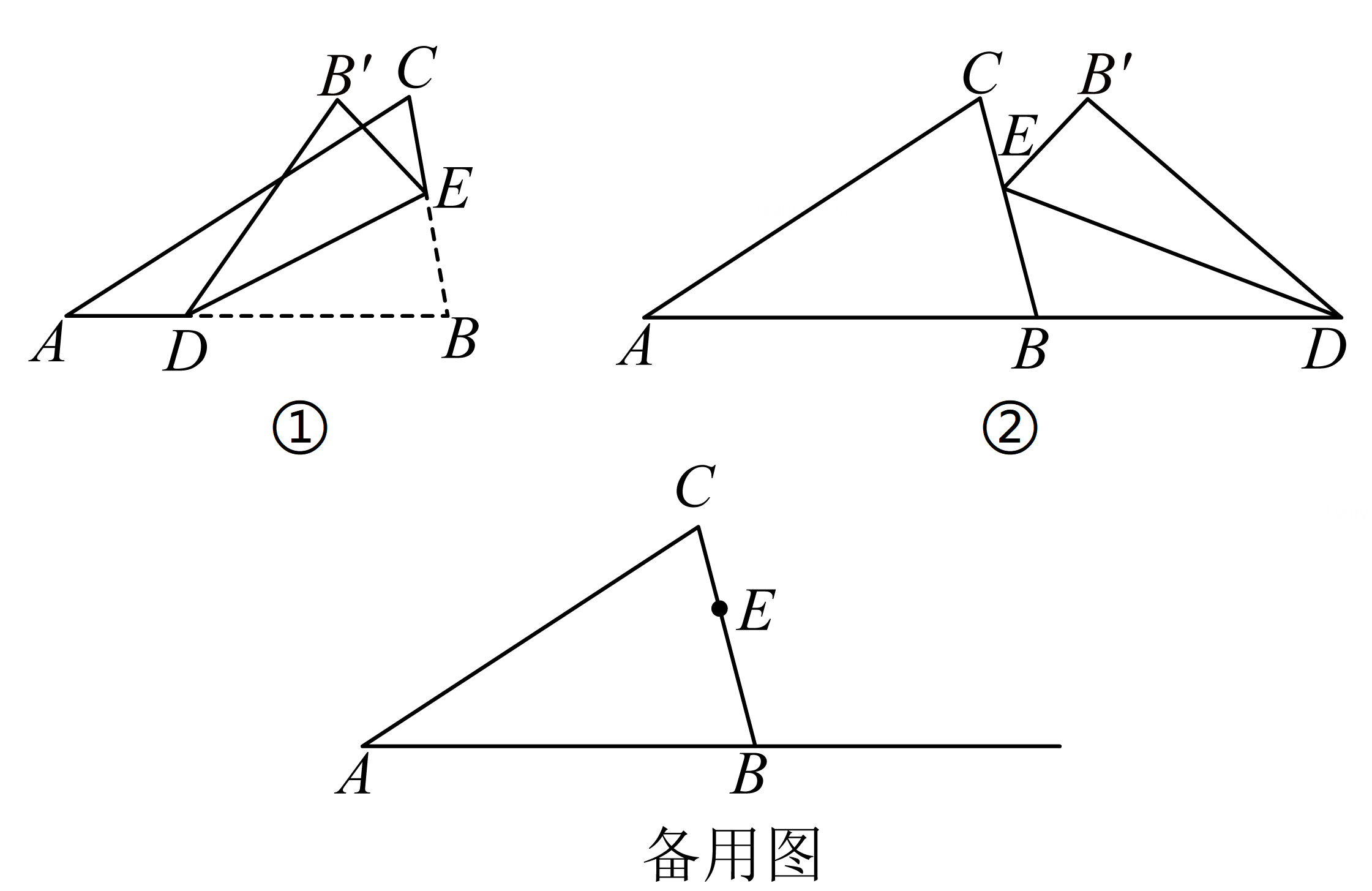 (1)、如图①,若∠ADB'=125°,求∠CEB'的度数;(2)、如图②.试探究∠ADB'与∠CEB'的数量关系,并说明理由;(3)、连接CB',当CB'∥AB时,直接写出∠CB'E与∠ADB'的数量关系为 .
(1)、如图①,若∠ADB'=125°,求∠CEB'的度数;(2)、如图②.试探究∠ADB'与∠CEB'的数量关系,并说明理由;(3)、连接CB',当CB'∥AB时,直接写出∠CB'E与∠ADB'的数量关系为 . -
4、如图,在四边形ABEC中,∠E和∠A都是直角,且AB=AC . 现将△BEC沿BC翻折,点E的对应点为E',BE'与AC边相交于D点,且BE'恰好是∠ABC的平分线,若CE=1,求BD的长.
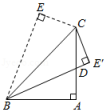
-
5、在△ABC中,D,E是BC边上的两点,且BA=BD,CA=CE,连接AD,AE.
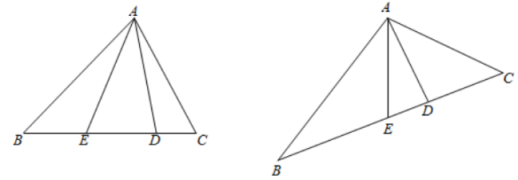 (1)、如图①,若∠B=40°,∠C=60°,求∠DAE的度数;(2)、如图②,若∠BAC=α(0°<α<180°),试说明:∠DAE=90°-α;(3)、若∠DAE=45°,则∠BAC=°.
(1)、如图①,若∠B=40°,∠C=60°,求∠DAE的度数;(2)、如图②,若∠BAC=α(0°<α<180°),试说明:∠DAE=90°-α;(3)、若∠DAE=45°,则∠BAC=°. -
6、如图,在△ABC中,AB=AC,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F.
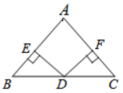 (1)、试说明:DE=DF;(2)、若∠BDE=40°,求∠BAC的度数.
(1)、试说明:DE=DF;(2)、若∠BDE=40°,求∠BAC的度数. -
7、如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,在空白小正方形中,选取2个涂上阴影,使6个阴影小正方形组成一个轴对称图形,请设计出四种方案.
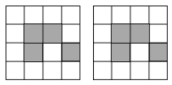

-
8、如图,已知在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,连接BD.
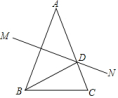 (1)、若∠A=40°,求∠DBC的度数;(2)、若AB=10,DC=3,求线段BD的长度.
(1)、若∠A=40°,求∠DBC的度数;(2)、若AB=10,DC=3,求线段BD的长度. -
9、如图,已知OA和OB两条公路以及C,D两个村庄,要在∠AOB的内部建立一个车站P,使车站到两个村庄距离相等,且P到OA,OB两条公路的距离相等.(要求:尺规作图,不写作法,保留作图痕迹)

-
10、如图,在正方形网格中,点A , B , C , M , N都在格点上.
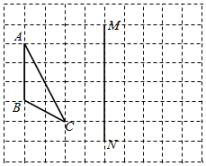 (1)、作△ABC关于直线MN对称的图形△A'B'C'.(2)、点P在直线MN上,当△PAC的周长最小时,P点在什么位置,在图中标出P点.
(1)、作△ABC关于直线MN对称的图形△A'B'C'.(2)、点P在直线MN上,当△PAC的周长最小时,P点在什么位置,在图中标出P点. -
11、 如图,点M,N分别在△ABC的边AB,AC的延长线上,∠MBC和∠NCB的平分线BP,CP相交于点P,PE⊥BC于点E,且PE=3 cm.若△ABC的周长为14 cm,S△BPC=7.5 cm2 , 则△ABC的面积为cm2 .

-
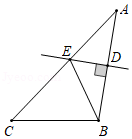
12、 如图,在△ABC中,AC=7,BC=4,AB的垂直平分线DE交AB于点D , 交AC于点E , 那么△BCE的周长为 .
-
13、 如图,在△ABC中,AB=AC,∠DBC=25°,且BD⊥AC,则∠A=°.

-
14、如图,△ABC和△AB'C'关于直线l对称,l交CC'于点D,AB=3,C'B'=1.5,CD=1,则五边形ABCC'B'的周长为 .

-
15、在长方形、正方形、等边三角形、等腰三角形中,对称轴条数最多的是.
-
16、 在“中 国 加 油 真 善 美”7个字中,是轴对称图形的是.
-
17、 如图,在等边三角形ABC中,E是AC边的中点,AD是∠BAC的平分线,P是AD上的动点,若AD=12 cm,则PE+PC的最小值为( )
 A、6 cm B、8 cm C、10 cm D、12 cm
A、6 cm B、8 cm C、10 cm D、12 cm -
18、如图,在4×4正方形网格中,将图中的2个小正方形涂上阴影,如果再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形是轴对称图形,那么符合条件的小正方形共有( )
 A、7个 B、8个 C、9个 D、10个
A、7个 B、8个 C、9个 D、10个 -
19、如图,E点在等腰三角形ABC底边上的高AD上,且BE⊥CE,若∠BAC=70°,则∠ABE的度数为( )
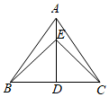 A、25° B、20° C、15° D、10°
A、25° B、20° C、15° D、10° -
20、 如图,在△ABC中,AC=3,BC=5,观察图中尺规作图的痕迹,则△ADC的周长是( )
 A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14