-
1、 如果关于 x 的一元二次方程 有两个不相等的实数根,那么 k 的取值范围是( )A、 B、 且 C、 D、 且
-
2、 将抛物线 向右平移 1 个单位后所得抛物线的解析式是( )A、 B、 C、 D、
-
3、 二次函数的二次项系数与一次项系数的和为( )A、2 B、-2 C、-1 D、-4
-
4、已知二次函数 .(1)、求证:该函数的图象与轴总有两个公共点;(2)、若该函数图象与轴的两个交点坐标分别为 , , 且 , 求证:;(3)、若 , , 都在该二次函数图象上,且 , 结合函数图象,写出的取值范围是 .
-
5、已知关于x的二次函数(1)、若该函数的图象与x轴的交点坐标是 , 求的值;(2)、若该函数的图象的顶点纵坐标为3,
①用含b的代数式表示c;
②当时,y的取值范围是 , 求c的取值范围.
-
6、已知二次函数的图象与y轴相交于点 .(1)、若 , 求该二次函数的最小值;(2)、若 , 点都在该函数的图象上,比较和的大小关系;(3)、若点都在该二次函数图象上,分别求的取值范围
-
7、已知二次函数的图象如图所示,则一次函数的图象大致为( )
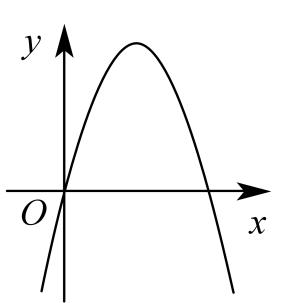 A、
A、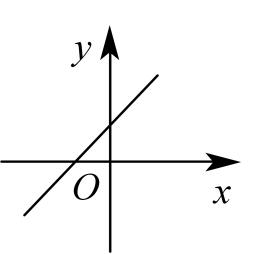 B、
B、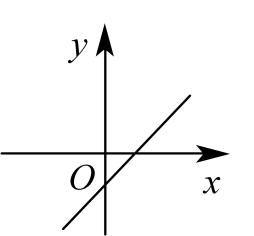 C、
C、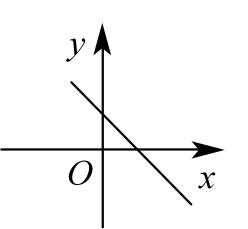 D、
D、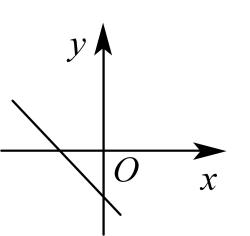
-
8、如图,已知二次函数的图象与轴交于点 , 与轴的交点在和之间(不包括这两点),对称轴为直线 , 下列结论:①;②;③;④;其中正确结论的个数有( )
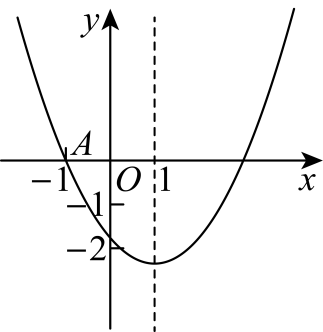 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
9、如图,二次函数( , , 为常数,)的图象与轴交于点 , 对称轴是直线 , 有以下结论:①;②若点和点都在抛物线上,则;③(为任意实数);④ . 其中正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
10、二次函数的自变量(表格中从左到右增大)与函数值的对应值如下表:
0
1
3
1
0
1
下列判断正确的是( )
A、 B、 C、 D、 -
11、用描点法画二次函数的图象时,列出了下面的表格:
从表中信息可得值为( )
A、 B、 C、 D、 -
12、抛物线上部分点的横坐标x , 纵坐标y的对应值如表:
x
…
0
1
2
…
y
…
5
0
…
从表中可知,下列说法中正确的是( ).
A、抛物线的对称轴是y轴 B、抛物线与x轴的一个交点为 C、函数的最小值为5 D、当时,y随x增大而减小 -
13、关于x的二次函数的图象下列说法不正确的是( )A、对称轴为直线 B、当时,图象上的最低点为 C、当时,y的值随x值的增大而增大 D、顶点一定在函数的图象上
-
14、下列关于二次函数的图象和性质的叙述中,正确的是( )A、与直线有两个交点 B、开口方向向上 C、对称轴是直线 D、点在函数图象上
-
15、已知二次函数 .
 (1)、求它的图象的顶点坐标和对称轴;(2)、画出它的图象.并结合图象,当时,则y的取值范围是 ▲ .
(1)、求它的图象的顶点坐标和对称轴;(2)、画出它的图象.并结合图象,当时,则y的取值范围是 ▲ . -
16、已知二次函数 , 完成下列各题:
 (1)、将函数关系式用配方法化为的形式,并写出它的顶点坐标、对称轴.(2)、求出它的图象与x轴的交点坐标.(3)、在直角坐标系中,画出它的图象.(4)、当为x何值时,函数y随着x的增大而增大?(5)、根据图象说明:当x为何值时,
(1)、将函数关系式用配方法化为的形式,并写出它的顶点坐标、对称轴.(2)、求出它的图象与x轴的交点坐标.(3)、在直角坐标系中,画出它的图象.(4)、当为x何值时,函数y随着x的增大而增大?(5)、根据图象说明:当x为何值时, -
17、在同一平面直角坐标系中,画出下列函数的图象:

①;②;③;④ .
从图象对比,说出解析式中二次项系数对抛物线的形状有什么影响?
-
18、在二次函数中,当时,y的取值范围是( )A、 B、 C、 D、
-
19、用配方法将二次函数化为的形式为( )A、 B、 C、 D、
-
20、/span>、为响应党中央关于打好精准扶贫攻坚战的号召,东部帮助西部进行扶贫产业开发,“食良品”是某市农产品商贸集团有限公司旗下的“消费扶贫”的电商平台,依托地理、集团专业等渠道的优势,基地直采,降低采购成本,全心全意为全市广大客户提供优质的食材,也解决了西部各地农副产品销售难的问题.目前,该平台为广大客户仅提供300元、500元、800元、1000元四种不同面额的提货券.随机抽查了其中100天的销售情况,整理统计后得到如下表一和表二:
表一
提货券每张面额(元)
300
500
800
1000
销售量(张)的百分比
30%
m%
18%
12%
表二
日均销售量(张)
300
450
500
650
天数
25
30
35
10
(1)、随机抽取一张提货券,面额不少于800元的概率是多少?(2)、哪种面额的提货券应多提供些?估计日均销售该面额的提货券多少张?(3)、估计月销售总额是多少元?(月以30天计算)