-
1、为方便游客观光游览,不少景区预增购一批“游览观光车”.某企业抓住机遇投资15万元购买并投放一批A型“游览观光车”,因需求量增加,计划继续投放B型观光车,B型观光车的投放数量与A型观光车的投放数量相同,投资总费用减少10%,其中B型观光车的单价比A型观光车的单价少30元,则A型观光车的单价是多少元?设A型观光车的单价为x元,根据题意列方程正确的是( )A、 B、 C、 D、
-
2、已知m=4n-4,则(m-4n)2-3(m-4n)-10的值是( )A、-6 B、6 C、18 D、-38
-
3、计算:的结果为( )A、 B、 C、1 D、-1
-
4、褐马鸡是我国的珍稀鸟类,如图是保护褐马鸡宣传牌上利用网格画出的褐马鸡的示意图.若建立适当的平面直角坐标系,表示嘴部点A的坐标为(-3,2),表示尾部点B的坐标为(2,0),则表示足部点C的坐标为( )
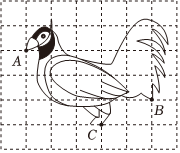 A、(0,1) B、(-1,-1) C、(0,-2) D、(0,-1)
A、(0,1) B、(-1,-1) C、(0,-2) D、(0,-1) -
5、某校801班要选拔一名跳绳成绩优异且发挥稳定的学生参加学校的跳绳比赛.如表是四名候选人十次一分钟跳绳测试成绩的平均数和方差,则应该选择( )号候选人参加比赛.
候选人序号
①
②
③
④
平均数(个)
198
212
205
212
方差(个)
3
3.2
4.5
1.8
A、① B、② C、③ D、④ -
6、下列代数式中,计算正确的是( )A、m3+m3=2m6 B、(mn)6=mn6 C、m2•m3=m6 D、(m3)3=m9
-
7、五边形内角和度数为( )A、270° B、450° C、540° D、900°
-
8、小宁与小波两位同学在学习“平行线”后进行了课后探究:
素材提供:“两块相同直角三角板,两条平行线”.三角板ABC与三角板DEF如图2所示摆放,其中∠ACB=∠DFE=90°,∠BAC=∠FDE=60°,l1∥l2 , 点A , B在直线l1上,点D , E在直线l2上.
动手实践:将三角板沿着直线平移或旋转能形成丰富的图形,也能得到许多有趣的结论.
问题解决:小宁将三角板ABC向右平移.
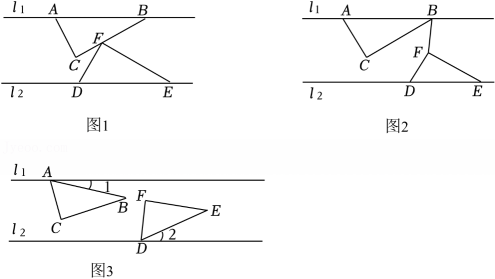 (1)、如图1,当点F落在线段BC上时,求∠BFE的度数.(2)、如图2,在三角板ABC向右平移过程中,连结BF(初始状态E , F , B三点在同一直线上),记∠BFE=α,∠CBF=β.
(1)、如图1,当点F落在线段BC上时,求∠BFE的度数.(2)、如图2,在三角板ABC向右平移过程中,连结BF(初始状态E , F , B三点在同一直线上),记∠BFE=α,∠CBF=β.①当点F在BC右侧时,试探究α与β的数量关系.
②小宁发现,当点F在BC左侧时,α与β的数量关系将发生改变,那么此时α与β的数量关系是 ▲ .
(3)、思维拓展:小宁和小波一起将两块三角板旋转,如图3,小宁将三角板ABC绕点A以每秒1°的速度顺时针旋转,同时小波将三角板DEF绕点D以每秒2°的速度逆时针旋转,设时间为t秒,∠1=t°,∠2=2t°,且0≤t≤60,若边AC与三角板DEF的一条边平行时,请直接写出所有满足条件的t的值. -
9、根据以下素材,探索完成任务.
有A、B两种卡纸,可用来做小旗子,若1张A卡纸和1张B卡纸共能做小旗子8面,2张A卡纸和3张B卡纸共能做小旗子19面.
(1)、求A、B两种卡纸.每张可分别做几面小旗子.(2)、由于艺术节场地布置的需要,某学校打算采购A、B两种卡纸.A卡纸每张4元,B卡纸每张3元,正好赶上商场促销活动:买一张A卡纸,就赠送一张B卡纸.学校计划用这两种卡纸共同做60面小旗子.①制作过程中,若A、B卡纸恰好充分利用,没有余料剩余,则做这些小旗子需要两种卡纸各多少张,并求出最低采购费用.
②由于艺术节实际需要,现须用卡纸再做灯笼42个.已知一张A、B卡纸可分别做灯笼3个和2个.请你结合方案评价表直接写出一种小旗子、小灯笼的制作数量方案(同一张卡纸只能做同一类手工,即不能既做小旗子又做小灯笼,采购费用低于65元).
由A卡纸制作
由B卡纸制作
小旗子(面)
小灯笼(个)
小旗子(面)
小灯笼(个)
方案评价表
方案等级
采购费用
制作中卡纸使用情况
评分
优秀
低于65元
两种卡纸均无余料剩余
3分
良好
低于65元
仅一种卡纸有余料剩余
2分
合格
低于65元
两种卡纸均有余料剩余
1分
-
10、(1)、已知关于x的分式方程 .
①当a=5时,求方程的解.
②若该方程去分母后所得的整式方程的解是增根,求a的值.
(2)、关于x的方程有整数解,求此时整数m的值. -
11、如图,方格纸中每个小正方形的边长都为1,△ABC的顶点均在方格纸的格点上,将△ABC经过一次平移后得到△A'B'C',图中标出了点C的对应点C' .
 (1)、请画出平移后的△A'B'C';(2)、若连接AA' , BB',则这两条线段的关系是 ;(3)、求线段BC扫过的面积.
(1)、请画出平移后的△A'B'C';(2)、若连接AA' , BB',则这两条线段的关系是 ;(3)、求线段BC扫过的面积. -
12、先化简 , 再从0,1,2,中选择一个合适的数代入并求值.
-
13、解下列方程组:(1)、;(2)、 .
-
14、如图,已知AB∥CD , 点E , F分别在直线AB , CD上,点P在AB , CD之间,EF的右侧,且∠EPF=60°.若将射线EA沿直线EP折叠得射线EA' , 射线FC沿直线FP折叠得射线FC' , EA'与FC'所在直线交于点H , 则∠EHF= .

-
15、在代数式求值时,可以利用交换律,将各项交换位置后,把一个多项式化成“(a2±2ab+b2)+其它项”的形式,然后利用完全平方公式得到“(a±b)2+其它项”,最后整体代入求值,例如对于问题“已知a+b=2,c=1,求a2+c2+b2+2ab的值”,可按以下方式求解:a2+c2+b2+2ab=a2+2ab+b2+c2=(a+b)2+c2=22+12=5.请仿照以上过程,解决问题:若m+n=3﹣t , n﹣k=t﹣7,则m2+4n2+k2+4mn﹣2mk﹣4nk+1= .
-
16、已知关于x , y的方程组 , 下列结论:①当这个方程组的解x , y的值互为相反数时,a=﹣2;②当a=1时,方程组的解也是方程x+y=4+2a的解;③无论a取什么实数,x+2y的值始终不变;④若用x表示y , 则;其中正确的有 .(请填上你认为正确的结论序号)
-
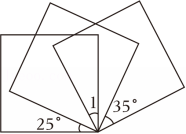
17、如图,将三张大小相同的透明正方形纸片的一个顶点重合放置,那么∠1的度数为 .
-
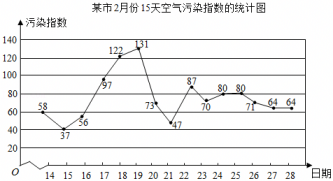
18、某市今年2月份15天的空气污染指数统计如图所示,若规定污染指数在0~50,51~100,101~150范围的空气质量依次为优,良,轻度污染,则这15天中,该市空气质量属优的有 天,它的频率是 .
-
19、如图是由4张纸片拼成的一个长方形,相邻纸片之间互相不重叠也无缝隙,其中①②是两个面积相等的梯形、③④是正方形,若想求出长方形的面积,则只需知道下列哪个条件( )
 A、①与②的周长之差 B、③的面积 C、①与③的面积之差 D、长方形周长
A、①与②的周长之差 B、③的面积 C、①与③的面积之差 D、长方形周长 -
20、如图,AB∥CD , EC分别交AB , CD于点F , C , 连接DF , 点G是线段CD上的点,连接FG . 若∠1=∠3,∠2=∠4,则结论①∠C=∠D;②FG⊥CD;③EC⊥FD中,正确的是( )
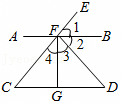 A、①② B、②③ C、①③ D、①②③
A、①② B、②③ C、①③ D、①②③