相关试卷

1、设m＝xy ， n＝x+y ， p＝x²+y² ， q＝x²﹣y² ，其中 ${\begin{cases} x = t + 2020 \\ y = t + 2018 \end{cases}$ ， ①当n＝3时，q＝6．②当p＝ $\frac{29}{2}$ 时，m＝ $\frac{21}{4}$ ．则下列正确的是（　　）

A、①正确②错误 B、①正确②正确 C、①错误②正确 D、①错误②错误

查看解析
2、分式 $\frac{x + 1}{x - 2}$ 的值（　　）

A、不能为﹣1 B、不能为0 C、不能为1 D、不能为2

查看解析
3、下列从左往右的变形，因式分解正确的是（　　）

A、（x﹣2）²＝x²﹣4x+4 B、x²﹣4x+4＝x（x﹣4）+4 C、x²﹣4x+4＝x²﹣4（x﹣1） D、x²﹣4x+4＝（x﹣2）²

查看解析
4、估计 $\sqrt{26} + 2$ 的值在（　　）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看解析
5、若0＜x＜1，则x^﹣¹、x、x²的大小关系是（　　）

A、x^﹣¹＜x＜x² B、x＜x²＜x^﹣¹ C、x²＜x＜x^﹣¹ D、x²＜x^﹣¹＜x

查看解析
6、在平面直角坐标系中，O为原点，△OAB是直角三角形， $∠ A O B = 9 0^{°}$ ， $O A = \frac{4 \sqrt{3}}{3}$ ， $O B = 4$ ，点A在y轴正半轴，点B在x轴正半轴，D点从O点出发，沿x轴正半轴方向运动，以OD为边在第一象限内作等边△ODE.

(1)、如图①，当E恰好落在线段AB上，求OE的长；

(2)、在(1)的条件下，把△OED沿x轴正方向平移得到 $Δ O^{^{'}} E^{^{'}} D$ ，点O，D，E的对应点分别为O'， $D^{^{'}}$ ， E'，线段A $D^{^{'}} E$ P和 $O^{^{'}} E^{^{'}}$ 与线段AB分别交于点F和点M，连接OF交OE'于点N.在平移过程中，
①设OO'的长为x，△O'D'E'与△AOB重叠部分的面积为y，试用含有x的代数式表示y，并直接写出x的取值范围；
②线段MN的长为▲；

(3)、点D在运动过程中，设OD的长为t，△ODE与△AOB重叠部分的面积为S，当S最大时，点D停止运动，将△AOB绕点O顺时针旋转得到△A'OB'，点A，B的对应点分别为A'，B'，连接EA'，EB'，直接写出△EA'B'面积的取值范围.

查看解析
7、我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”

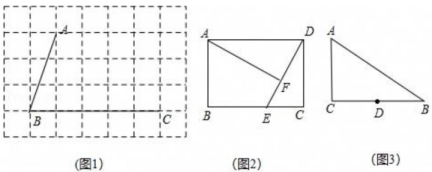(1)、已知：如图1，四边形ABCD的顶点A，B，C在网格格点上，请你在如下的 $5 \times 7$ 的网格中画出1个不同形状的等邻边四边形ABCD，要求顶点D在网格格点上.

(2)、如图2，矩形ABCD中， $A B = \frac{20}{7}$ ， $B C = 5$ ，点E在BC边上，连接DE画AF交DE于点F，若 $D E = \frac{5}{4} C D$ ，找出图中的等邻边四边形并说明理由；

(3)、如图3，在 $R t △ A B C$ 中， $∠ A C B = 9 0^{°}$ ， $A B = 4$ ， $A C = 2$ ， D是BC的中点，点M是AB边上一点，当四边形ACDM是“等邻边四边形”时，求BM的长.

查看解析
8、如图，一次函数 $y_{1} = k x + b$ 与反比例函数 $y_{2} = \frac{n}{x}$ 的图象相交于 A(1， 3)，B(3， m).

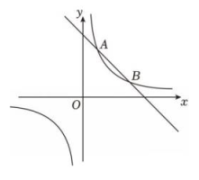(1)、分别求两个函数的解析式；

(2)、在 x 轴上找一点 P，使得 $△ O A P$ 的面积为 6，求出 P 点坐标；

(3)、根据图象，直接写出不等式 $k x + b < \frac{n}{x}$ 的解集.

查看解析
9、已知二次函数 $y = 2 (x - 1) (x - m - 3)$ (m 为常数).

(1)、求证：不论 m 为何值，该函数的图象与 x 轴总有公共点；

(2)、当 m 取什么值时，该函数的图象与 y 轴的交点在 x 轴的上方？

查看解析
10、浙江新能源汽车数量不断上升，据相关信息，2025年全省将建成公共充电桩超230万个. 某小区为优化公共充电桩管理，随机记录了某日50辆新能源汽车的充电情况.
时间段
6点-10点
10点-14点
14点-18点
18点-22点
22点-6点
数量(辆)
4
20
a
10
12
价格(元/度)
1.15
0.60
1.20
0.90
0.55

(1)、填空： $a =$ .

(2)、本次调查的50辆新能源汽车用电价格的众数为元/度，中位数为元/度.

(3)、若该地区每天需要充电的新能源汽车数量约为10万辆，请估计在6点至10点时间段内进行充电的新能源汽车数量.

查看解析
11、如图， $△ A B C$ 中，D是AB上一点， $A B = 16$ ， $A D = 4$ ， $A C = 8$ ，求证： $∠ A C D = ∠ B$ .

查看解析
12、在矩形 ABCD 中， $A B = 4$ ， $A D = 8$ ，点 P 是射线 BC 上一动点，连接 PD，作线段 PD 的垂直平分线，分别交 AD 所在直线与点 E，交 BC 所在直线于点 F，PD 与 EF 交于点 O，连接 PE、 DF。连接 BD，当点 P 在射线 BC 上移动时，当 $△ B P D$ 是等腰三角形时，则 PF 长为

查看解析
13、如图，已知点A在反比例函数 $y = \frac{k}{x} (x < 0)$ 上，作 $R t △ A B C$ ，点D为斜边AC的中点，连DB并延长交y轴于点E. 若 $△ B C E$ 的面积为8，则 $k =$

查看解析
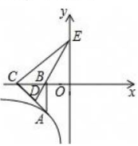
14、已知开口向下的抛物线 $y = a x^{2} - 3 x + a^{2} - 2 a - 3$ 经过坐标原点，那么 a 等于.

查看解析
15、已知一组数据 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 、 $x_{4}$ 、 $x_{5}$ 的平均数是 5，方差为 2，则另一组新数据 $2 x_{1} + 1$ 、 $2 x_{2} + 1$ 、 $2 x_{3} + 1$ 、 $2 x_{4} + 1$ 、 $2 x_{5} + 1$ 的方差是.

查看解析
16、若点 $A (- 1, y_{1})$ 和点 $B (2, y_{2})$ 均在二次函数 $y = 2 x^{2} + m$ 的图象上，则 $y_{1}$ $y_{2}$ （填“>”、“<”或“=”）.

查看解析
17、如图，正方形 ABCD 中，已知 $A B = 6 \sqrt{2}$ ，对角线 AC 与 BD 交于点 O，点 E 为射线 OB 上的一个动点（不与点 B 重合），点 M 为线段 ED 的中点. 现将线段 OM 绕点 M 顺时针旋转 $9 0^{°}$ 得到线段 MF，连结 AE， EF， AF， OF. 在点 E 的运动过程中，当 $A E = 2 O F$ 时，则线段 BE 的长为（）

A、 $6 \sqrt{3} - 6$ B、 $3 \sqrt{3} - 3$ C、 $6 \sqrt{3} - 6$ 或 $6 \sqrt{3} + 6$ D、 $3 \sqrt{3} - 3$ 或 $3 \sqrt{3} + 3$

查看解析
18、如图，点A在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交于A，B两点，点A在第一象限. 点C在x轴正半轴上，连接AC交反比例函数图象于点D. AE为 $∠ B A C$ 的平分线. 过点B作AE的垂线，垂足为E，连接DE. 若 $A C = 3 D C$ ， $△ A D E$ 的面积为 8，则k的值为（）

A、4 B、6 C、8 D、12

查看解析
19、如图，在 x 轴的上方，直角 $∠ B O A$ 绕原点 O 按顺时针方向旋转，若 $∠ B O A$ 的两边分别与函数 $y = - \frac{1}{x}$ 、 $y = \frac{2}{x}$ 的图象交于 B、A 两点，则 $∠ O A B$ 的大小的变化趋势为（）

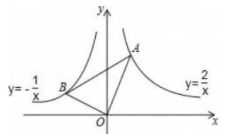A、先减小后增大 B、先增大后减小 C、不变 D、无法确定

查看解析
20、已知一个二次函数 $y = a x^{2} + b x + c$ 的自变量 x 与函数 y 的几组对应值如下表：
x
…
-4
-2
0
3
5
…
y
…
-24
-8
0
-3
-15
…
则下列关于这个二次函数的结论正确的是（）

A、图象的开口向上 B、当 $x > 0$ 时，y 的值随 x 的值增大而增大 C、图象经过第二、三、四象限 D、图象的对称轴是直线 $x = 1$

查看解析

上一页 11 12 13 14 15 下一页跳转

时间段	6点-10点	10点-14点	14点-18点	18点-22点	22点-6点
数量(辆)	4	20	a	10	12
价格(元/度)	1.15	0.60	1.20	0.90	0.55

x	…	-4	-2	0	3	5	…
y	…	-24	-8	0	-3	-15	…