-
1、如图,在中,已知 , 将绕点A按逆时针方向旋转后得到 , 则图中阴影部分的面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图,在平面直角坐标系中,点A在x轴负半轴上,点B在y轴正半轴上,经过四点, , , 则圆心点D的坐标是( )
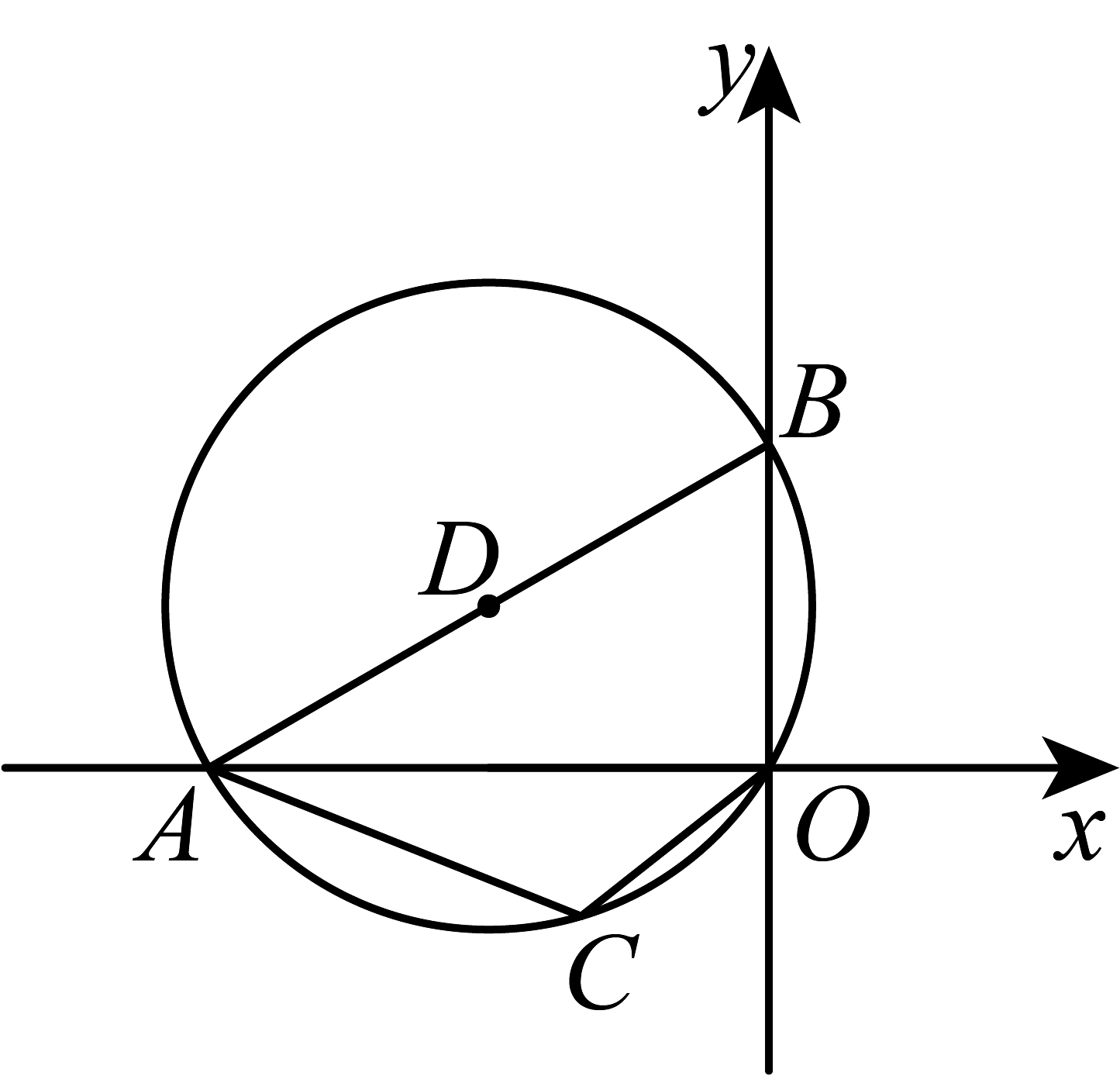 A、 B、 C、 D、
A、 B、 C、 D、 -
3、如图所示,矩形纸片中, , 把它分割成正方形纸片和矩形纸片后,分别裁出扇形和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则的长为( )
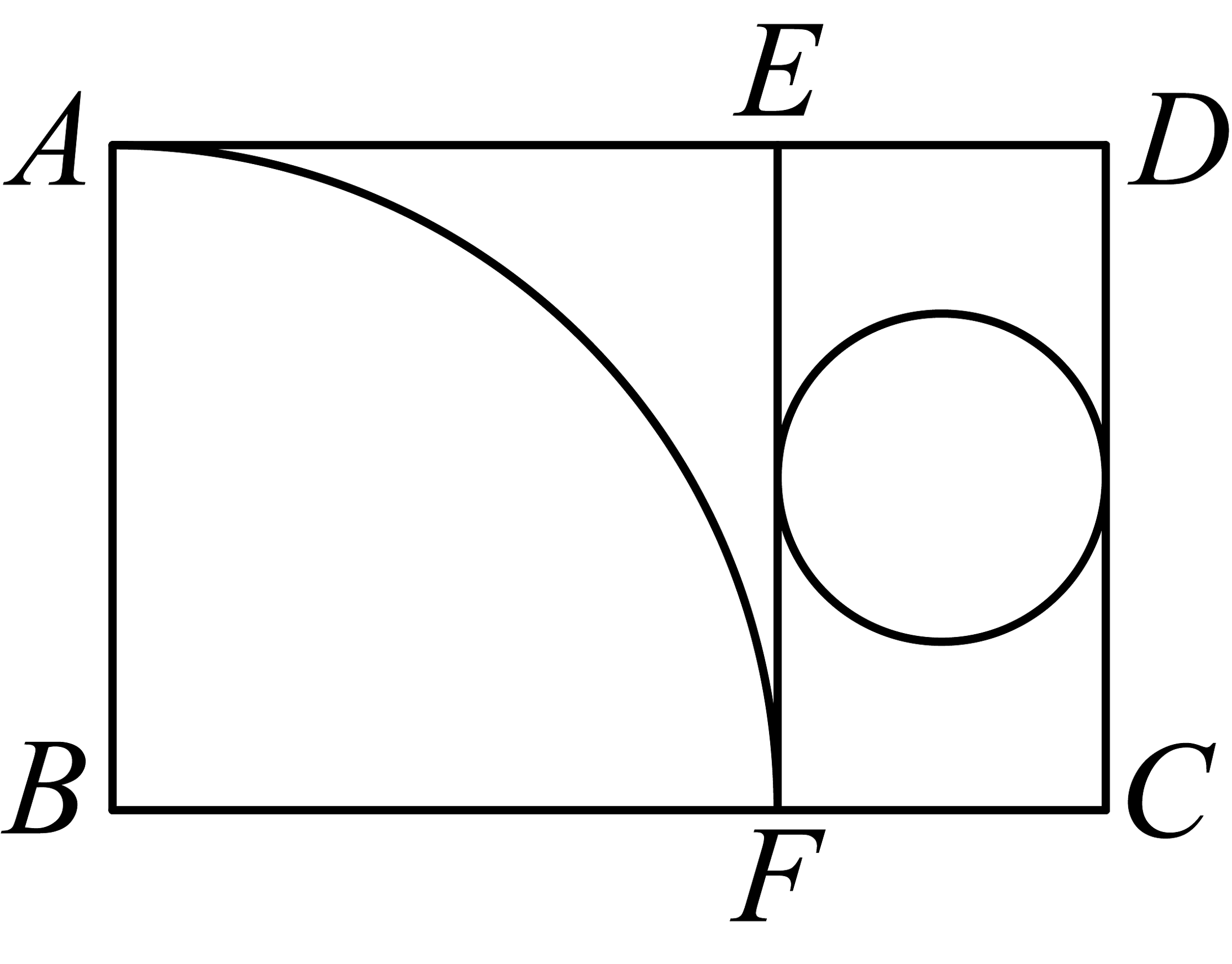 A、 B、 C、 D、
A、 B、 C、 D、 -
4、已知圆的内接正三角形的边心距是1,则这个三角形的边长是( )A、 B、 C、2 D、
-
5、如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
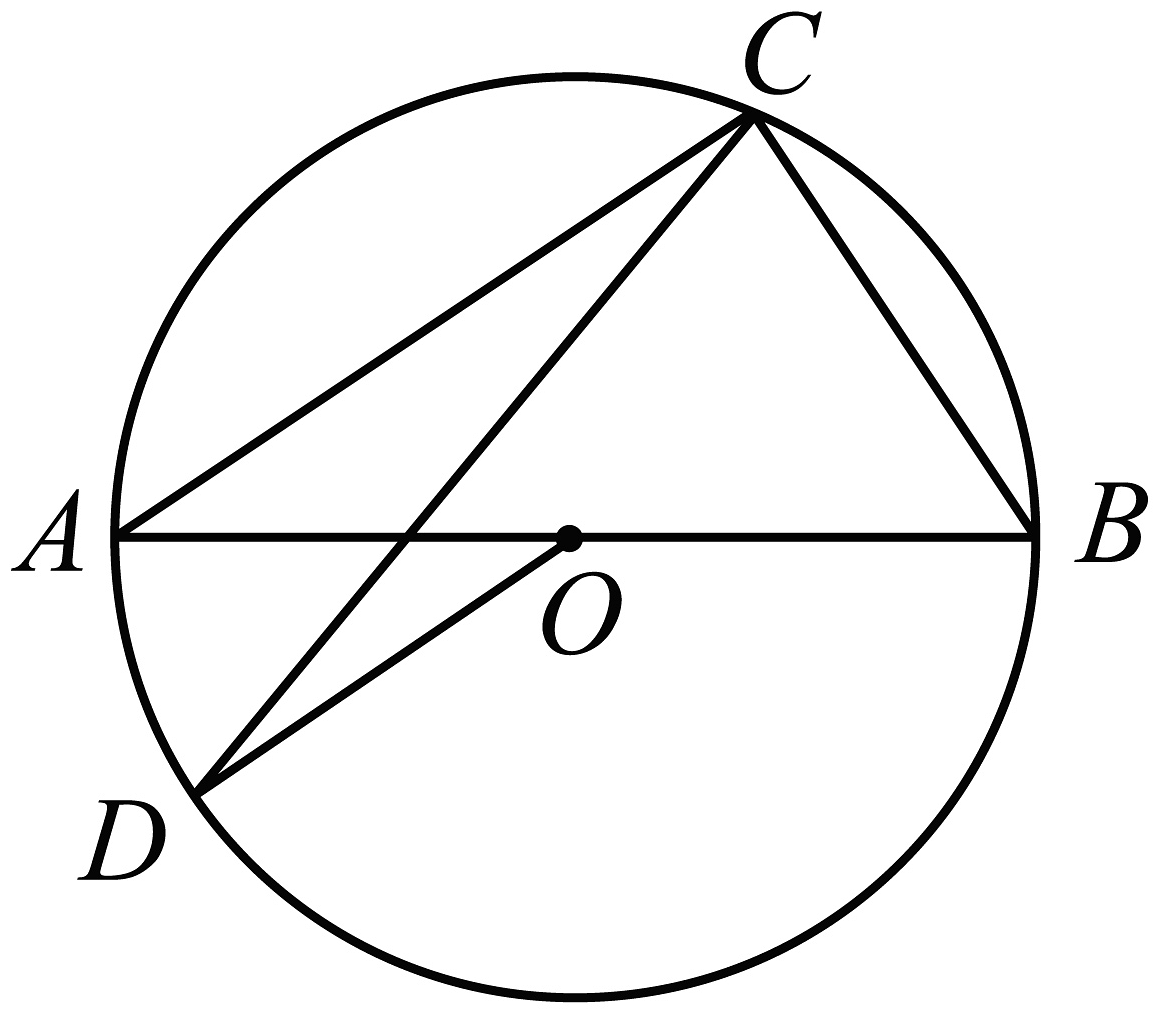 A、20° B、30° C、40° D、70°
A、20° B、30° C、40° D、70° -
6、如图,在中,半径垂直于弦 , 垂足为C, , 则等于( )
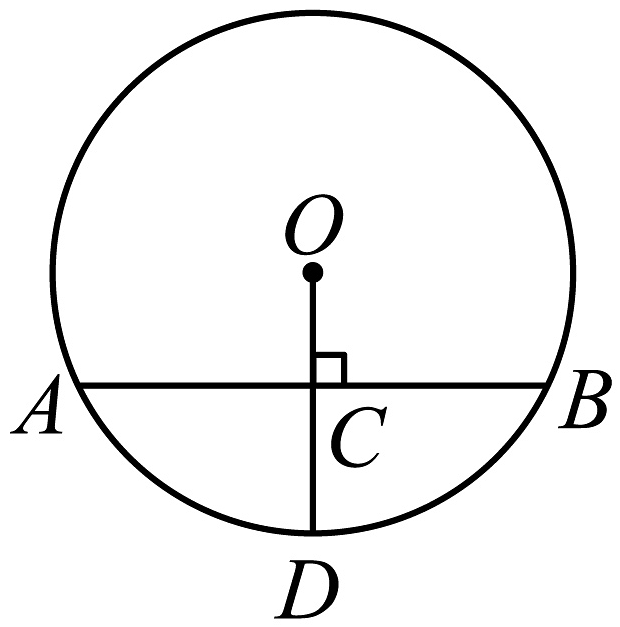 A、 B、 C、 D、
A、 B、 C、 D、 -
7、如图,在△ABC中,AB=BC=2,以AB为直径的⊙O与BC相切于点B,则AC的长为( )
 A、 B、 C、2 D、2
A、 B、 C、2 D、2 -
8、如图,A,B,C是上的三点,且 , 则的度数是( )
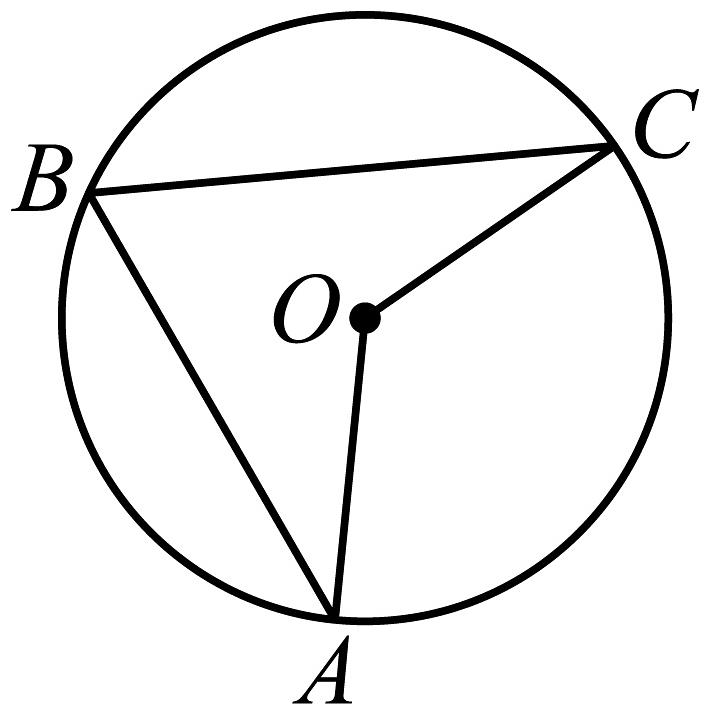 A、 B、 C、 D、或
A、 B、 C、 D、或 -
9、如图,与关于成中心对称,下列结论中不成立的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、将二次函数的图象向右平移4个单位长度,再向上平移5个单位长度后,所得图象对应的函数解析式是( )A、 B、 C、 D、
-
11、下列方程是一元二次方程的是( )A、 B、 C、 D、
-
12、综合与实践:【问题情境】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系.数学活动课上,王老师出示了一个问题:点、在数轴上分别表示有理数、 , 则在数轴上、两点之间的距离为 . 如:表示为3与1两数在数轴上所对应的两点之间的距离;表示为3与两数在数轴上所对应的两点之间的距离.

利用数形结合思想回答下列问题:
(1)数轴上表示2和7两点之间的距离是______;数轴上表示2和的两点之间的距离是______;
【解决问题】:
(2)数轴上表示和的两点之间的距离表示为______.
(3)试用数轴探究:当时的值为______.
【实践探究】利用绝对值的几何意义,结合数轴,探究:
(4)利用数轴求出的最小值为______,并写出此时可取的整数值为______.
-
13、【阅读材料】“整体思想”是中学数学解题中的一种重要的思想方法,运用“整体思想”的方法在求代数值中非常重要,有这样一道题:
代数式:的值为9,则代数式的值为.
小明在做作业时采用的方法如下:
由题意得 , 则有 .
所以
.
所以代数式的值为9.
【方法运用】
(1)、若 , 则______.(2)、若代数式的值为15,求代数式的值. -
14、一天下午,某出租车以希望小学为出发点在东西方向营运,行车情况依先后次序记录如下(向东为正方向,单位:):
, , , , , , , .
(1)、将最后一名乘客送到目的地,出租车在出发点位置的东边还是西边?离出发点多远?(2)、若出租车在行驶过程中,每千米耗油升,出租车一下午共耗油多少升? -
15、小明同学在学习完有理数的运算后,对运算产生了浓厚的兴趣,她借助有理数的运算,定义了一种新运算“”,运算规则为: . 如:(1)、求的值;(2)、求的值.
-
16、已知互为相反数,互为倒数,是最大的负整数,求的值.
-
17、在数轴上表示下列各数,并用“<”把这些数连接起来.

;3.5;; .
-
18、计算:(1)、(2)、
-
19、如果电梯上升5米,记作+5米,那么下降8米可记作米.
-
20、根据流程图中的运算程序,当输入数据时,输出结果为( )
 A、9 B、 C、25 D、
A、9 B、 C、25 D、