-
1、【问题背景】
如图1,已知正方形的边长为 , 点是边上的一点,把沿直线对折后,点落在点处.
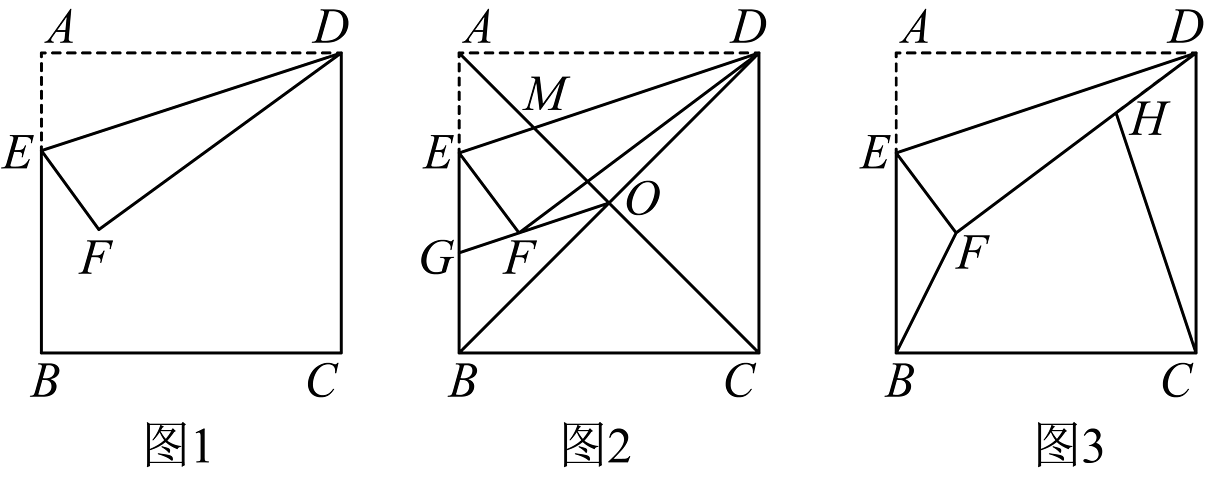
【问题探究】
(1)如图2,当时,正方形的对角线与相交于点 , 与正方形另一条对角线相交于点 , 连接并延长,交线段于点 .
①证明点是的中点;
②试探究与有怎样的关系,并说明理由.
【拓展延伸】
(2)如图3,点是线段上的一点,且 , 连接、 . 在点从点运动到点的过程中,求的最小值.
-
2、在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“合成矩形”.如图为点P,Q的“合成矩形”的示意图.
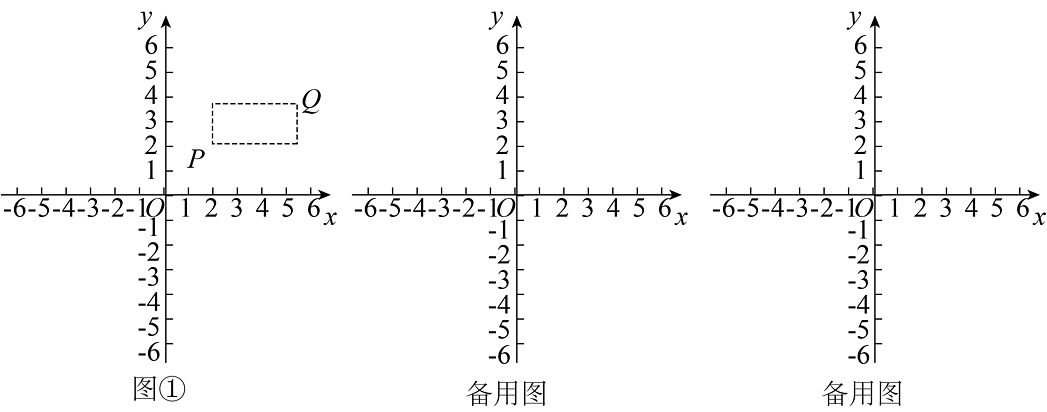 (1)、若A点坐标为(2,0),
(1)、若A点坐标为(2,0),①当B点坐标为(5,1)时,点A,B的“合成矩形”的面积是______;
②若点C在y轴上,且点A,C的“合成矩形”为正方形,则直线AC的表达式为______;
③若点P在直线y=﹣2x+2上,且点A,P的“合成矩形”为正方形,求P点的坐标;
(2)、点O的坐标为(0,0),点D为直线y=x+b(b≠0)上一动点,若O,D的“合成矩形”为正方形,且此正方形面积不小于2时,求b的取值范围. -
3、如图,直线与轴交于点 , 与轴交于点 , 直线与轴交于点 , 与直线交于点 , 过点作轴于点 . 点是轴上一动点,过作轴的垂线,分别与直线 , 交于点 , .
 (1)、设的长为 , 点的横坐标为 , 求与的函数表达式;(2)、若以 , , , 为顶点的四边形是平行四边形,求的值.
(1)、设的长为 , 点的横坐标为 , 求与的函数表达式;(2)、若以 , , , 为顶点的四边形是平行四边形,求的值. -
4、如图,在矩形中, , , 为的中点,为上一动点,为中点,连接 , 则的最小值是( )
 A、2 B、4 C、 D、
A、2 B、4 C、 D、 -
5、如图, , , 三点共线,与交于点 , , 若 , 则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、“七巧板”是我国古代的一种拼图玩具,由5块等腰直角三角形,1块正方形和1块平行四边形薄板组成.如图①是小明用正方形纸板制作的七巧板,图②是用该七巧板拼出的狐狸图案的飞镖盘,若小明每次扔飞镖时,飞镖都能掷在狐狸上,则随机投掷一次,掷在狐狸头部的概率是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、如图,已知 , 则等于( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、围棋起源于中国,古代称之为“弈”,至今已有4000多年的历史.下面是对战棋谱中的四个部分,由黑白棋子摆成的图案是轴对称图形的是( )A、
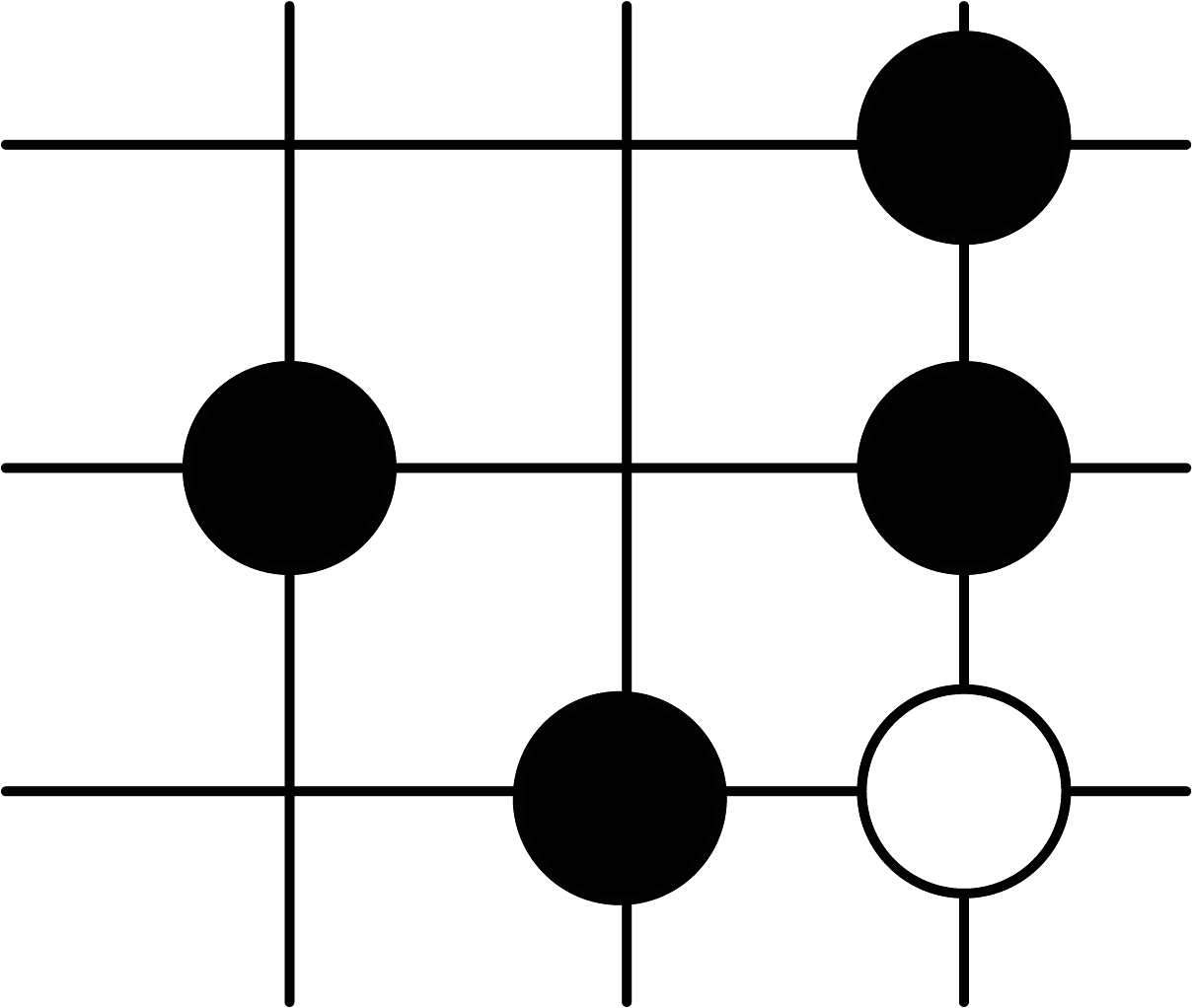 B、
B、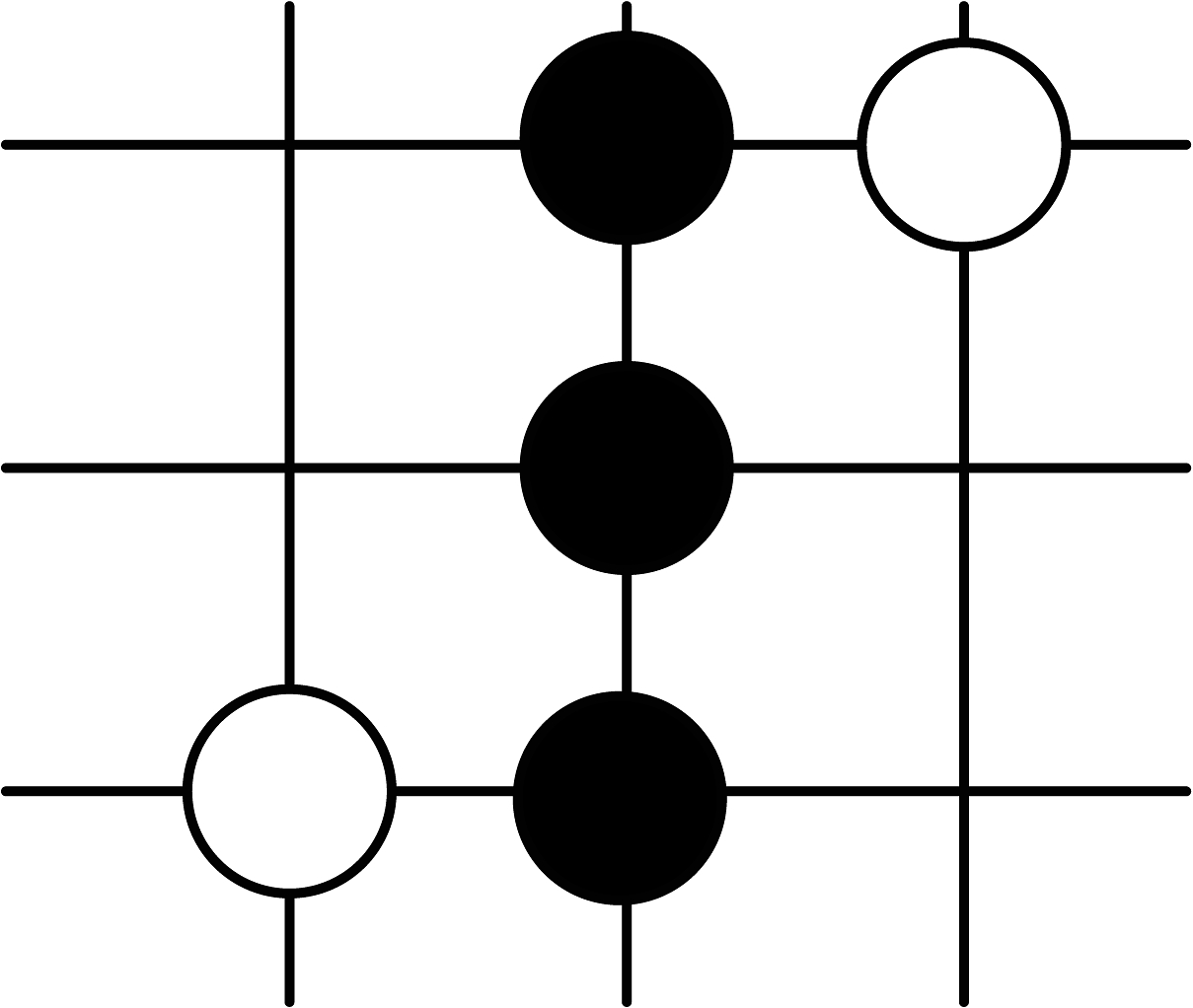 C、
C、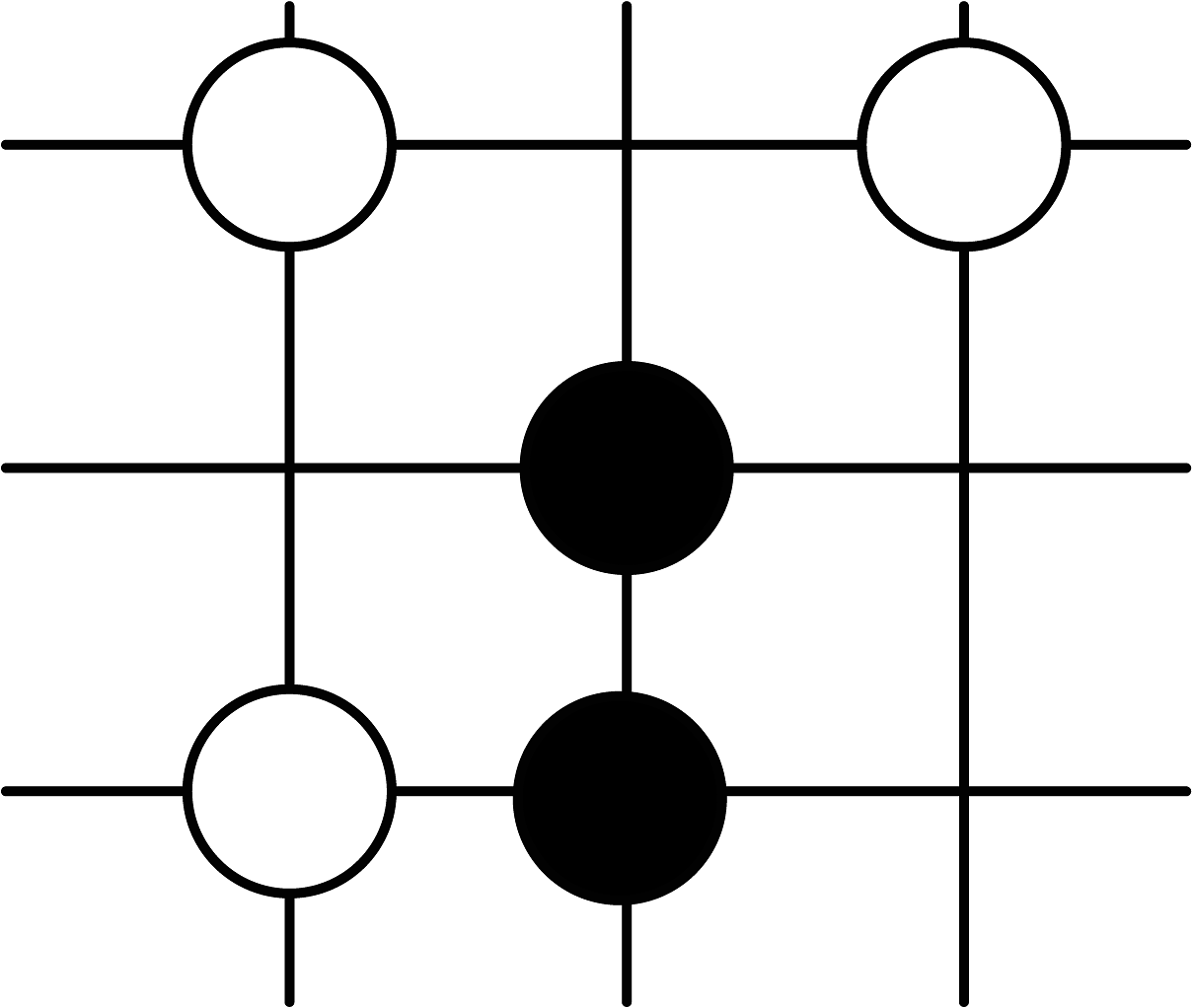 D、
D、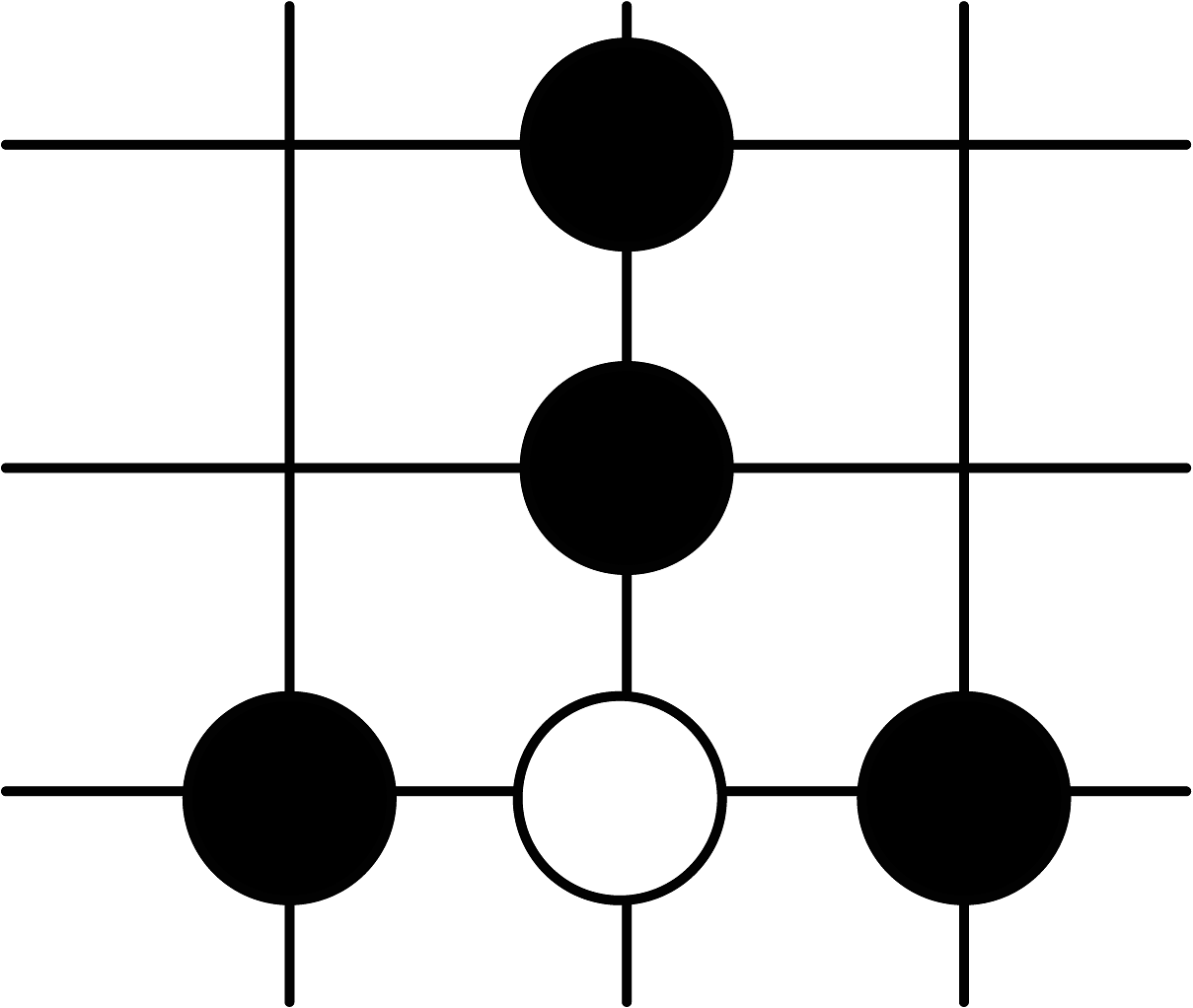
-
9、学习“旋转”这章书后,老师让大家用两个全等三角形纸片动手操作探究问题;已知 , , .
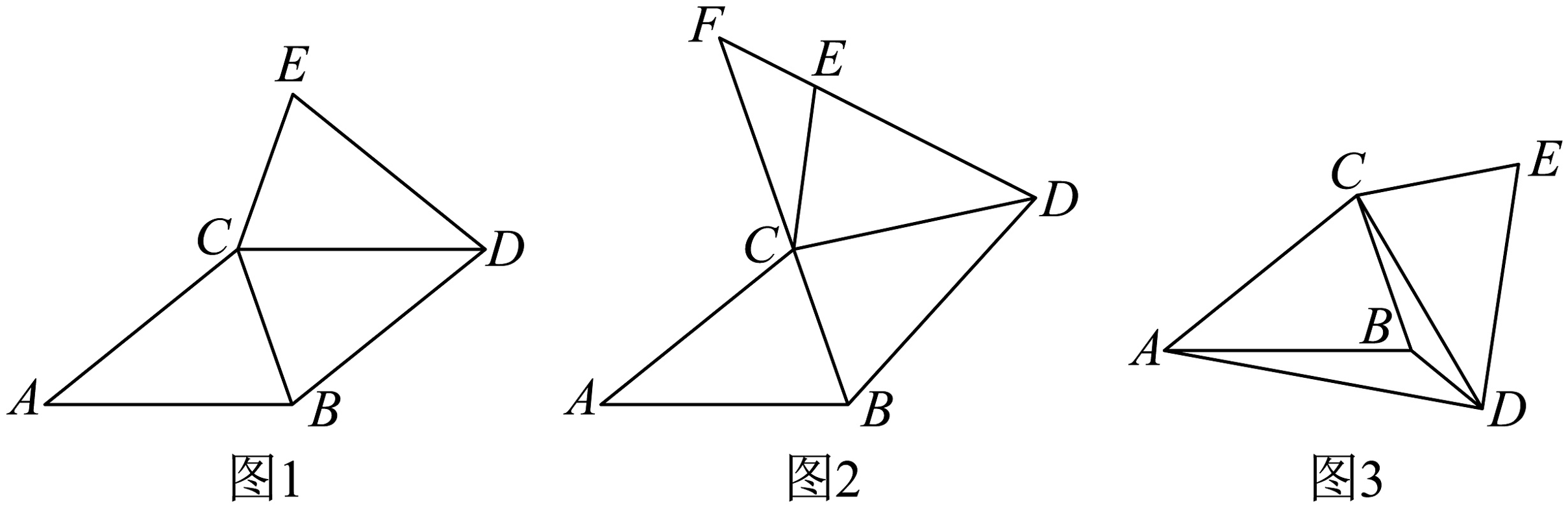 (1)、“兴趣小组”如图1所示放置和 , 使得平分 , 请判断四边形是哪种特殊的四边形,并证明你的结论.(2)、“智慧小组”利用“兴趣小组”的图形继续探究:在(1)的基础上将(1)中的绕点C逆时针旋转(旋转角小于),使得与的延长线相交于点F.请证明此时 .(3)、“创新小组”则是将(1)中的绕点C顺时针旋转(旋转角小于),若 , 请直接写出的度数.
(1)、“兴趣小组”如图1所示放置和 , 使得平分 , 请判断四边形是哪种特殊的四边形,并证明你的结论.(2)、“智慧小组”利用“兴趣小组”的图形继续探究:在(1)的基础上将(1)中的绕点C逆时针旋转(旋转角小于),使得与的延长线相交于点F.请证明此时 .(3)、“创新小组”则是将(1)中的绕点C顺时针旋转(旋转角小于),若 , 请直接写出的度数. -
10、阅读材料:若 , 求与的值.
解:∵ ,
∴ ,
∴ ,
∴ , ,
∴ , .
根据你的观察,探究下面的问题:
(1)、已知 , 求与的值.(2)、已知的三边长 , , 都是正整数,且满足 , 求的周长. -
11、如图,某男生推铅球,铅球出手(点处)的高度是 , 出手后的铅球沿一段抛物线运行,当运行到最高时,水平距离 . 求出这条抛物线所表示的函数解析式.

-
12、如图,在平面直角坐标系中,点的坐标为 , 点B的坐标为 , 点C的坐标为 .
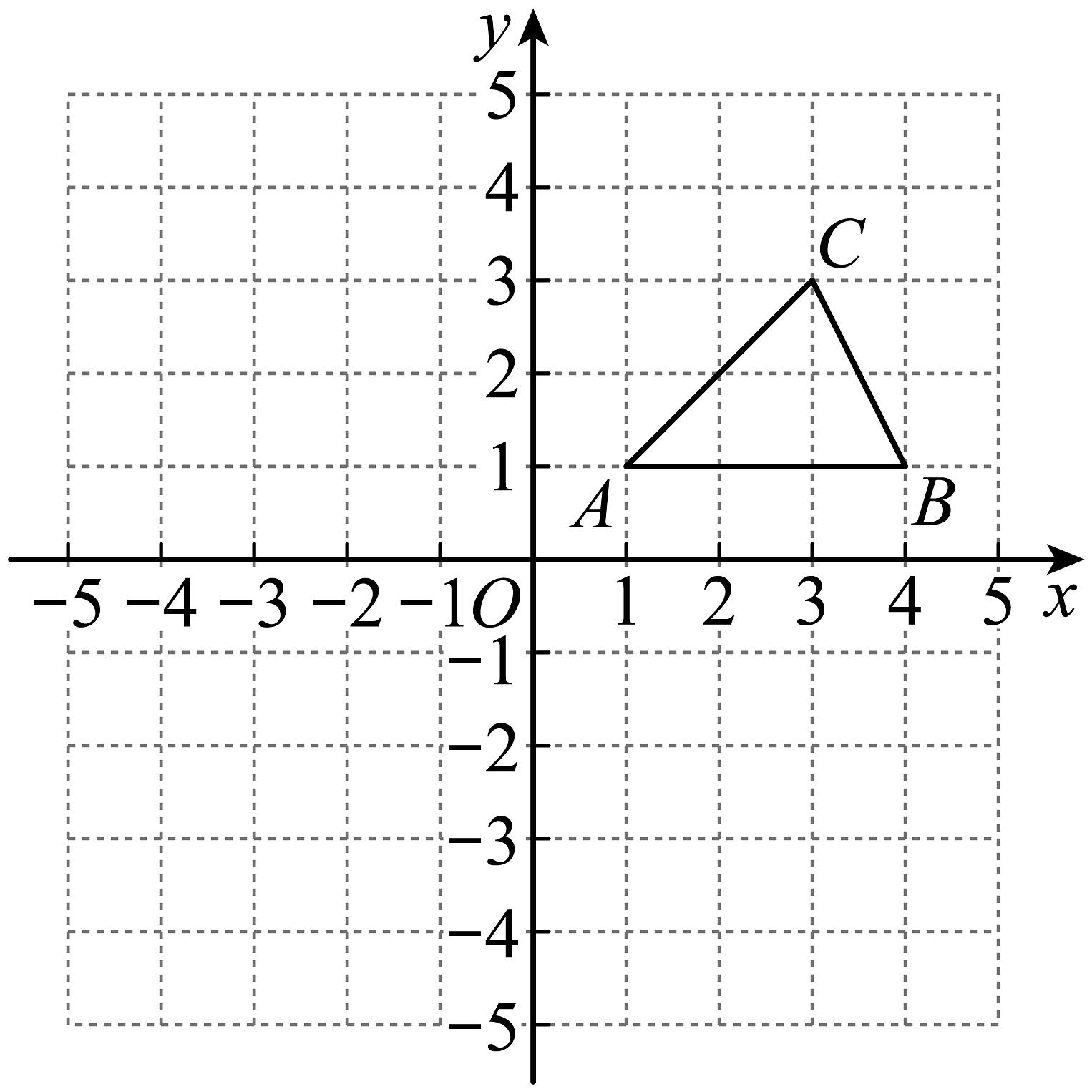 (1)、画出将绕原点O逆时针旋转后得到的 , 并写出的坐标.(2)、写出点关于原点O对称的点的坐标.
(1)、画出将绕原点O逆时针旋转后得到的 , 并写出的坐标.(2)、写出点关于原点O对称的点的坐标. -
13、如图是二次函数的图象,根据图象回答以下问题
 (1)、抛物线的对称轴是直线____________;(2)、当____________时,二次函数有最____________值(填大或小),是____________;(3)、当____________时,随的增大而增大.
(1)、抛物线的对称轴是直线____________;(2)、当____________时,二次函数有最____________值(填大或小),是____________;(3)、当____________时,随的增大而增大. -
14、解方程:
-
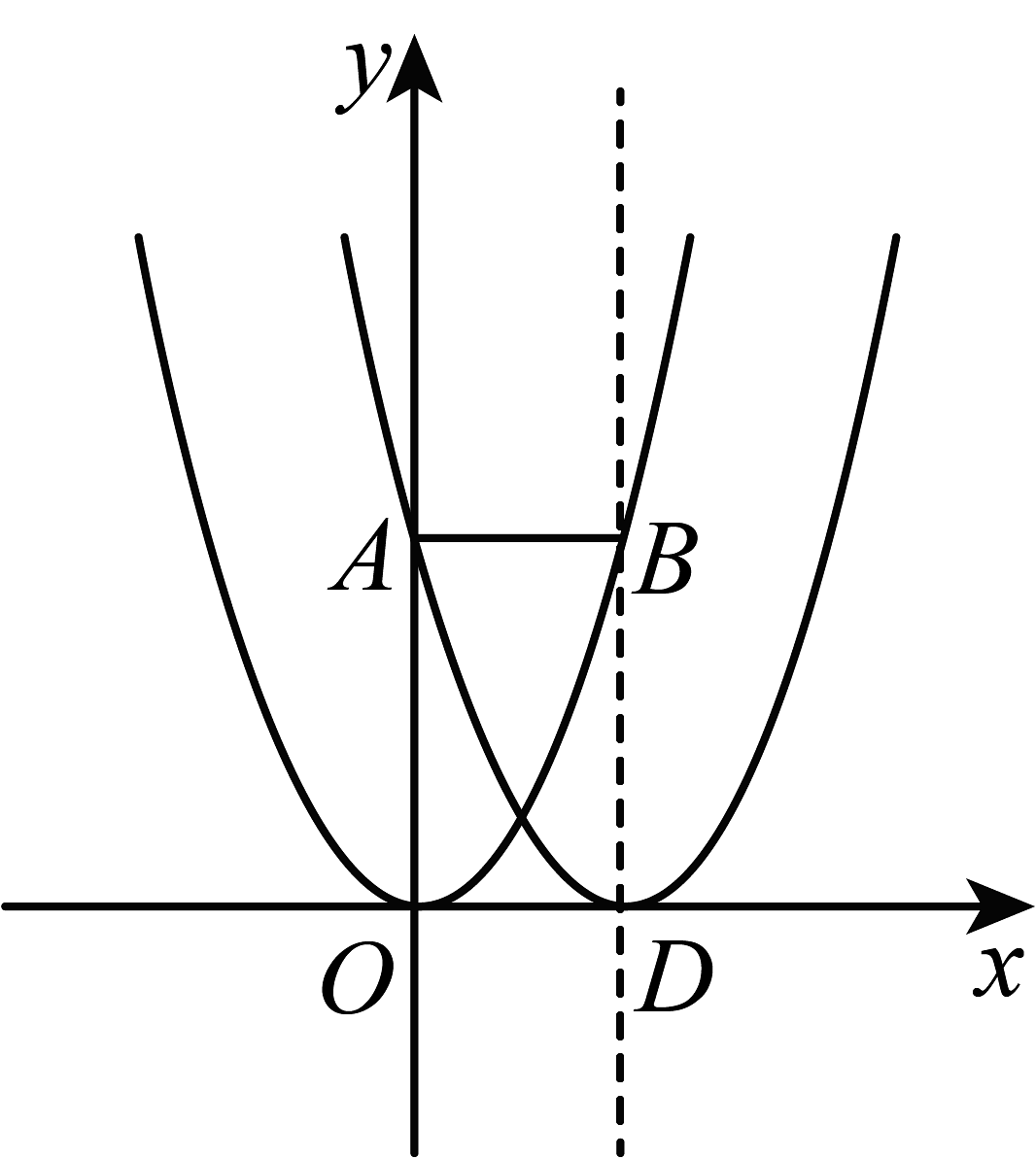
15、如图,将二次函数的图象向右平移2个单位长度,所得新拋物线的顶点为D,并与y轴交于点A,对称轴与函数的图象的交点为 , 若新抛物线存在点P使以D为底的等腰三角形,则点P的坐标为 .
-
16、某地进行“迎国庆振兴杯”篮球邀请赛,赛制为单循环(每两队之间赛一场),若计划安排21场比赛,则邀请个球队参赛.
-
17、已知点与点关于原点对称,则点的坐标为 .
-
18、小明用公式法解方程 , 请帮他填空第一步,解: , , .
-
19、拋物线的对称轴是轴.
-
20、如图是抛物线图象的一部分,抛物线的顶点是点 , 对称轴是直线 , 且抛物线与轴的一个交点为;直线的解析式为 , 下列结论:①;②;③方程有一个实数根;④抛物线与轴的另一个交点是;⑤当时,则 , 其中正确的是( )
 A、①②③ B、③⑤ C、①④ D、④⑤
A、①②③ B、③⑤ C、①④ D、④⑤