-
1、计算:(1)、()÷();(2)、(﹣1)4×|﹣8|+(﹣2)3×()2;
-
2、将连续的奇数1,3,5,7,9…,排列成如图所示数表:
任意圈出如图所示的5个数,设中间的一个数为a,则这5个数之和是(用含a的代数式表示).

-
3、若 , , 则的值等于
-
4、计算:﹣3+|﹣7|= .
-
5、如图,正六边形(每条边长相等、每个角相等)在数轴上的位置如图所示,点 , 对应的数分别为 , . 现将正六边形绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点所对应的数为1,像这样连续翻转后数轴上2025这个数所对应的点是( )
 A、点 B、点 C、点 D、点
A、点 B、点 C、点 D、点 -
6、若有理数 , , 在数轴上的位置如图所示,则化简的结果为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、一款羽绒服的成本价为a元,销售价比成本价增加了15%,现因库存积压,所以就按销售价的75%出售,那么这款羽绒服每件的实际售价为( )A、(1+15%)(1+75%)a元 B、75%(1+15%)a元 C、(1+15%)(1-75%)a元 D、(1+15%+70%)a元
-
8、下列计算中正确的是( )A、 B、 C、 D、
-
9、如图,在中,动点从点出发,沿折线向终点运动,在上的速度为每秒个单位长度,在上的速度为每秒个单位长度.当点不与点重合时,以为边在点的右上方作等边 , 设点的运动时间为(秒),与重叠部分的面积为 .
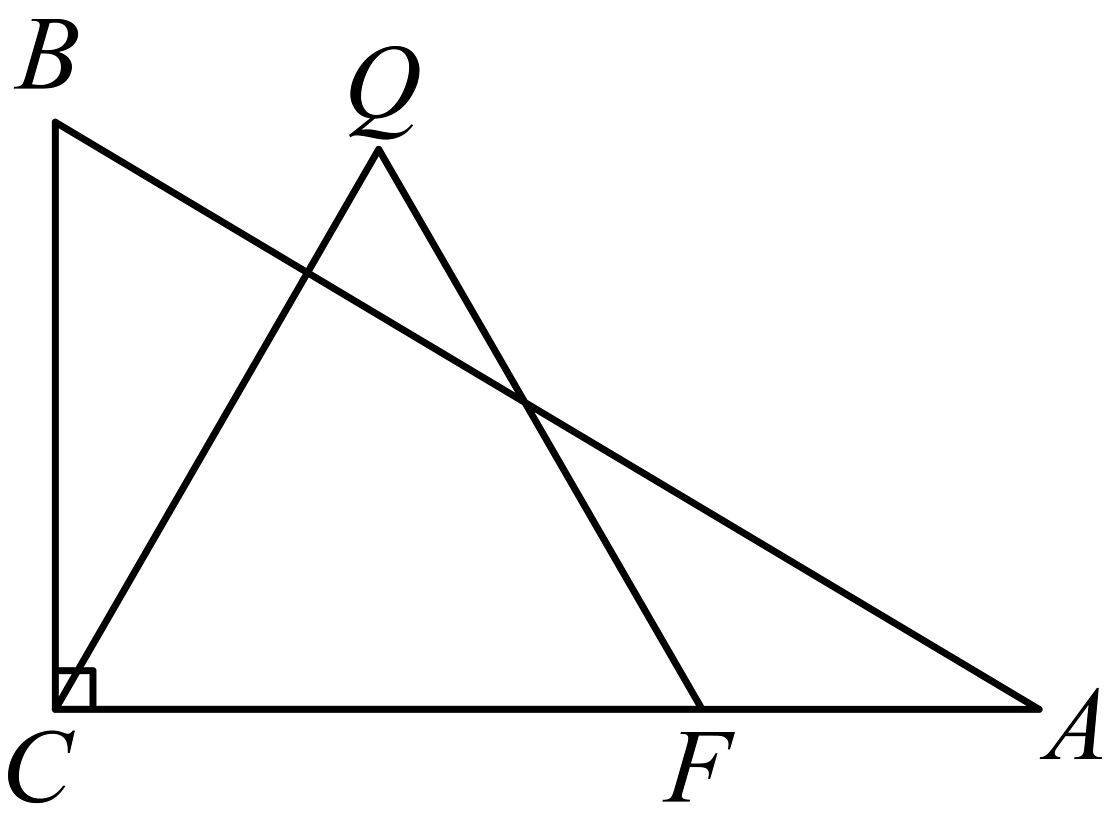 (1)、______(2)、求与之间的函数关系式,并写出的取值范围;(3)、取边的中点 , 连接 , 当是直角三角形时,直接写出的值.
(1)、______(2)、求与之间的函数关系式,并写出的取值范围;(3)、取边的中点 , 连接 , 当是直角三角形时,直接写出的值. -
10、已知抛物线( , 为常数)经过点和 .(1)、求该抛物线的函数表达式;(2)、将抛物线( , 为常数)向右平移个单位长度得到一个新的抛物线,若新的抛物线的顶点关于原点对称的点也在抛物线( , 为常数)上,求的值.
-
11、如图,抛物线与直线y=bx+c的两个交点分别为A(﹣2,4),B(1,1).
 (1)、求两个函数的解析式;(2)、点P在y轴上,且△ABP的面积是△ABO面积的2倍,求点P的坐标.
(1)、求两个函数的解析式;(2)、点P在y轴上,且△ABP的面积是△ABO面积的2倍,求点P的坐标. -
12、如图,在矩形空地上,修建两条平行于 边、一条平行于边的小路,条路等宽,其余部分铺草坪.已知的长为 , 的长为 , 铺草坪的单价是元 , 铺草坪的总价为元,求每条小路的宽度.

-
13、已知,在平面直角坐标系中,的三个顶点坐标分别为 , , .
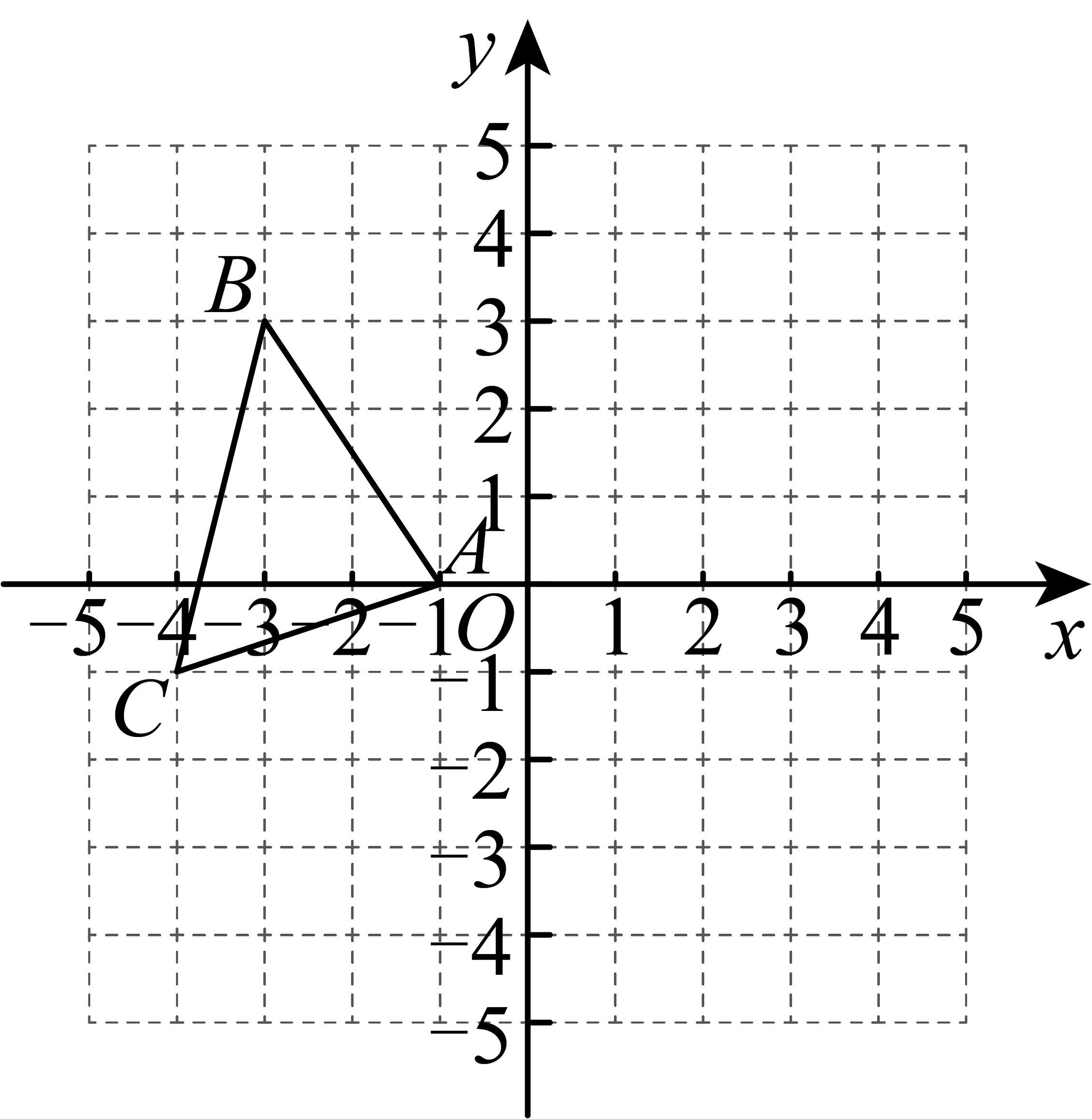 (1)、画出关于原点对称的 , 并写出点A的对应点的坐标;(2)、画出绕点O按逆时针方向旋转90°后的图形 , 并写出点C的对应点的坐标.
(1)、画出关于原点对称的 , 并写出点A的对应点的坐标;(2)、画出绕点O按逆时针方向旋转90°后的图形 , 并写出点C的对应点的坐标. -
14、已知抛物线 .(1)、若此抛物线的顶点在直线 上,求的值;(2)、若点 与点在此抛物线上,且直接写出的取值范围.
-
15、已知抛物线 在对称轴右侧呈下降趋势,其中 .(1)、求抛物线的对称轴;(2)、二次函数有最大值还是最小值?请求出这个最值.
-
16、如图,在 中, 将 绕点C顺时针旋转55°得到 ,于点D,求 的度数

-
17、解方程: .
-
18、如图,P、Q分别是⊙O的内接正五边形的边AB.BC上的点,BP=CQ,则∠POQ= .

-
19、火炮发明于中国,是指利用机械能、化学能(火药)、电磁能等能源抛射弹丸,射程超过单兵武器射程,由炮身和炮架两大部分组成的武器.在某次训练中,向上发射一枚炮弹,经x秒后的高度为y米,且y与x的关系式为若此炮弹在第6秒和第14秒时的高度相等,则此炮弹飞行第秒时的高度是最高的.
-
20、若关于的一元二次方程无实数根,则整数的最大值为 .