-
1、如图,在平面直角坐标系xOy中,正方形OABC的顶点A,C分别在x轴,y轴上,OA=3.
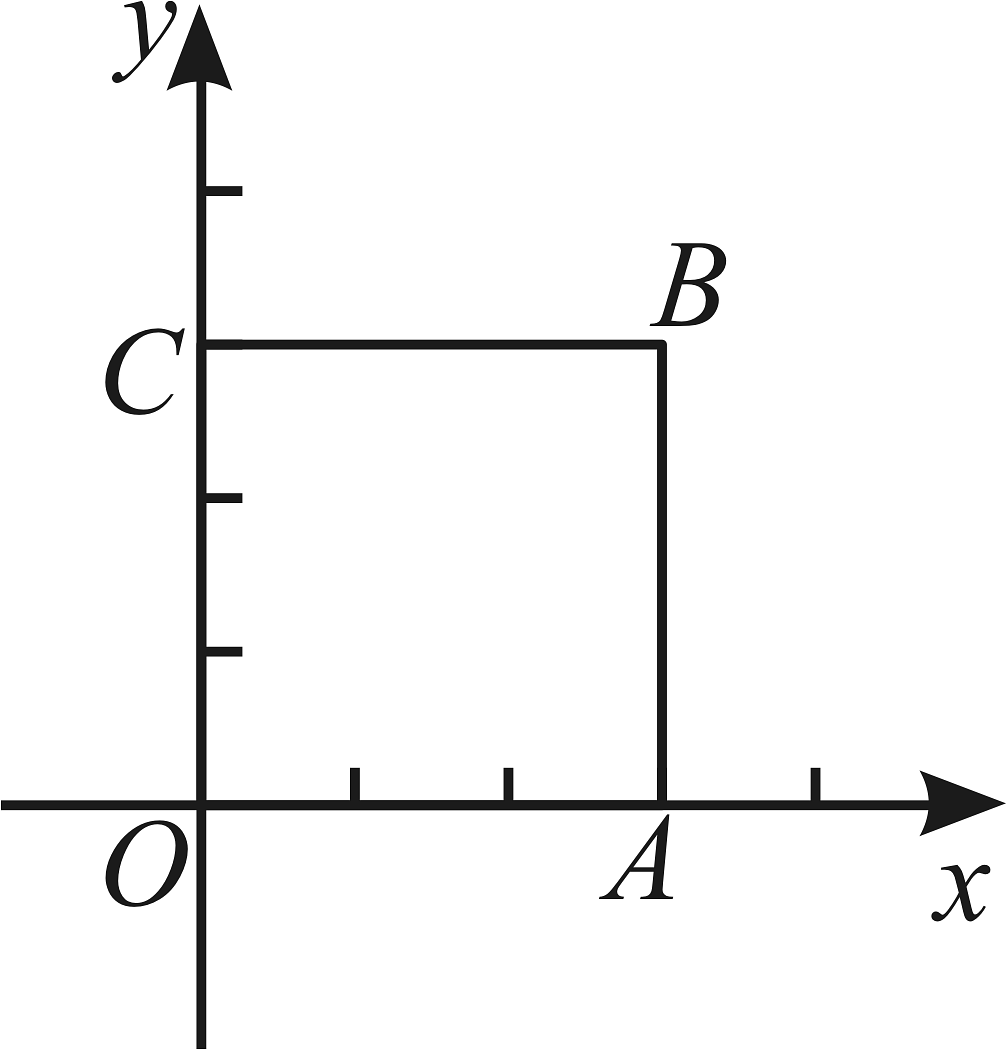 (1)、求直线OB的表达式;(2)、若直线y=x+b与该正方形有两个公共点,请直接写出b的取值范围.
(1)、求直线OB的表达式;(2)、若直线y=x+b与该正方形有两个公共点,请直接写出b的取值范围. -
2、在如图的正方形网格中,每个小正方形的边长为1,格点(顶点是网格线的交点的三角形)的顶点A,C的坐标分别为 , .
 (1)、在网格平面内画出平面直角坐标系;(2)、作出关于y轴对称的;(3)、求出的面积.
(1)、在网格平面内画出平面直角坐标系;(2)、作出关于y轴对称的;(3)、求出的面积. -
3、如图,在中,点是边上一点,连接 . 若 , , , , .
 (1)、求的度数;(2)、求的长.
(1)、求的度数;(2)、求的长. -
4、已知的立方根是 , 的算术平方根是4,求的值.
-
5、计算:(1)、(2)、
-
6、如图,在△ABC中,AB=AC=13,BC=10,D是AB的中点,过点D作DE⊥AC于点E,则DE的长是.

-
7、已知某汽车装满油后油箱中的剩余油量y(升)与汽车的行驶路程x(千米)之间具有一次函数关系(如图所示).为了行驶安全考虑,邮箱中剩余油量不能低于5升,那么这辆汽车装满油后至多行驶千米,就应该停车加油.

-
8、计算的结果为 .
-
9、一次函数与的图象如图所示,下列结论中正确的有( )
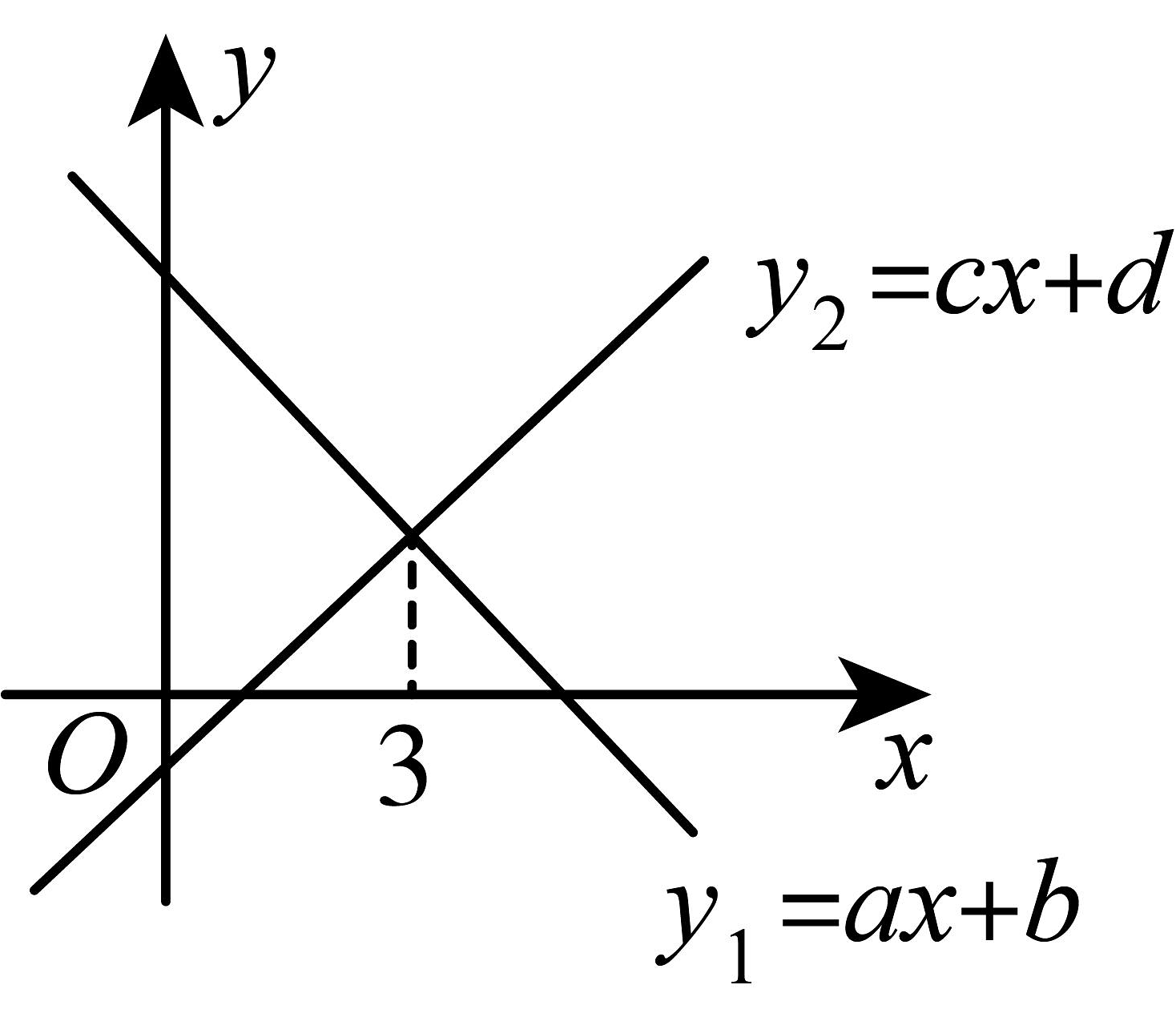
①对于函数来说,y随x的增大而减小;②函数的图象不经过第一象限;③;④ .
A、1个 B、2个 C、3个 D、4个 -
10、图1是某品牌畅销的冰箱,图2是它的侧面矩形示意图,对角线米,高与宽的长度比为 , 则冰箱的宽的长度为( )
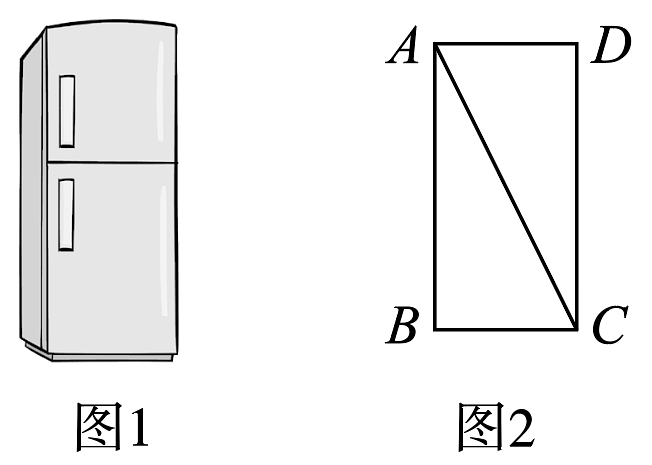 A、0.5米 B、0.6米 C、0.7米 D、0.8米
A、0.5米 B、0.6米 C、0.7米 D、0.8米 -
11、若一次函数(k,b是常数,且)的图像如图所示,则一次函数的图像不经过( )
 A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、第一象限 B、第二象限 C、第三象限 D、第四象限 -
12、若 , 则实数a在数轴上的对应点一定在( )A、原点左侧 B、原点或原点左侧 C、原点右侧 D、原点或原点右侧
-
13、若点P在第二象限,且到两条坐标轴的距离都是4,则点P的坐标为( )A、 B、 C、 D、
-
14、已知正比例函数的图象如图所示,则k的值为( )
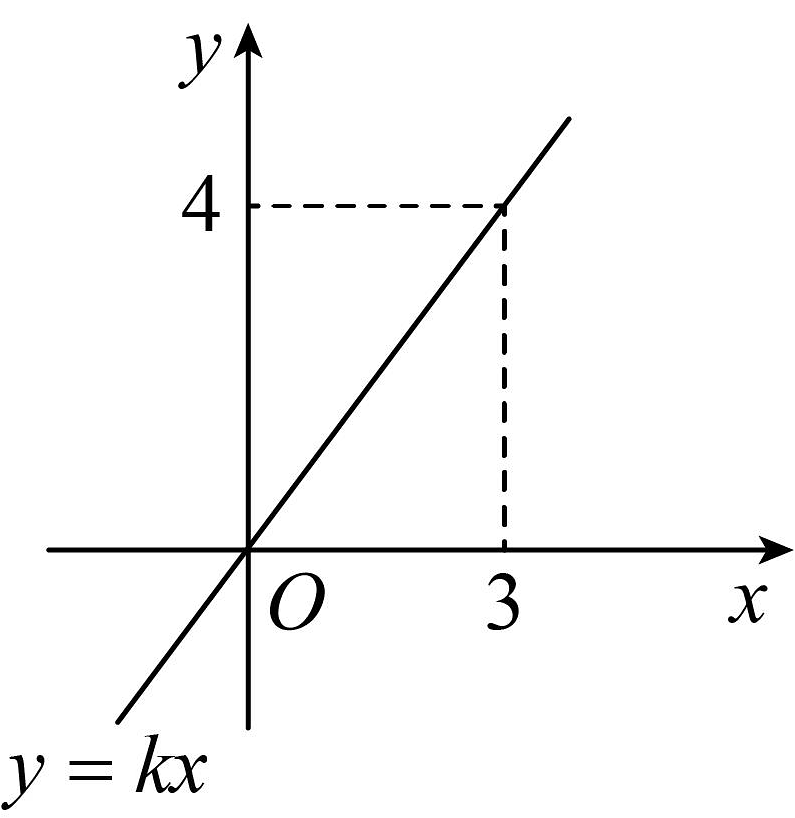 A、12 B、 C、 D、
A、12 B、 C、 D、 -
15、小明和妈妈去电影院看电影,电影票上写着“3排2座”,小明学了有序数对后,把“3排2座”记作 , 那么妈妈的电影票“5排3座”应记作( )A、 B、 C、 D、
-
16、下列各选项中是无理数的是( )A、 B、2023 C、 D、
-
17、某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.从甲、乙两个仓库到A,B两个果园的运价如下表所示:
甲仓库
乙仓库
到A果园
每吨15元
每吨25元
到B果园
每吨20元
每吨20元
设从甲仓库运往A果园x吨有机化肥.
(1)、从甲仓库运往B果园______吨有机化肥;从乙仓库运往A果园______吨有机化肥,运往B果园______吨有机化肥(用含x的式子表示,填最简结果);(2)、求从这两个仓库往两个果园运送有机化肥的总运费(用含x的式子表示);(3)、当时,求从这两个仓库往两个果园运送有机化肥的总运费. -
18、某供电局路线检修班乘汽车沿南北方向检修路线,检修班的记录员把当天行车情况记录如下:
到达地点
起点
前进方向
北
南
北
北
南
北
南
北
南
北
所走路程(km)
0
10
4
6
2
5
12
3
9
10
7
(1)、求地与起点之间的路程有多少千米;(2)、若汽车每千米耗油0.12升,这天检修班从起点开始,最后到达地,一共耗油多少升?(精确到0.1升) -
19、规定符号表示a,b两个数中较小的一个,规定符号表示a,b两个数中较大的一个.例如 ,(1)、计算:;(2)、化简:
-
20、数轴上的点 , , , 分别表示 , 的倒数,0的相反数, .(1)、在如图所示的数轴上描出 , , , 四个点;
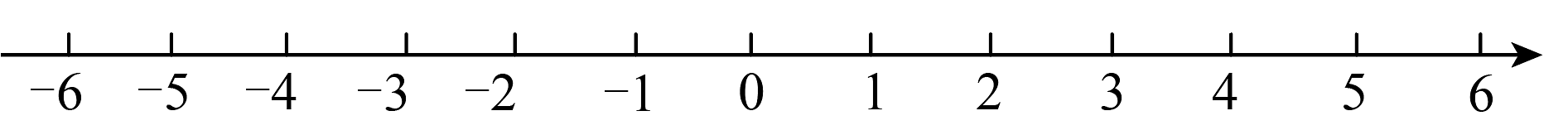 (2)、 , 两点间的距离是多少? , 两点间的距离是多少?
(2)、 , 两点间的距离是多少? , 两点间的距离是多少?