-
1、对于二次函数的图象,下列说法正确的是( )A、开口向下 B、对称轴是直线 C、当时,随的增大而减小 D、函数的最大值为4
-
2、一元二次方程的两根为和3,则的值是( )A、-3 B、3 C、-2 D、2
-
3、抛物线的顶点坐标是( )A、 B、 C、 D、
-
4、(1)呈现问题
如图①,在中, , D、E分别在、上,若 , 则和是顶角相等的等腰三角形,连接、 , 则、、之间的数量关系是________;与的数量关系是________;
(2)类比探究
如图②,和均为等边三角形,点A、E、D在同一直线上,连接 . 求出的度数及与的数量关系;
(3)拓展延伸
如图③,和均为等腰直角三角形, , 点A、E、D在同一直线上,为中边上的高,连接 . 直接写出的度数及线段、、之间的数量关系;
(4)解决问题
在(3)的条件下,若 , , 直接写出四边形的面积.

-
5、【教材呈现】
教材P49-复习题13题:已知 , , 求的值.
【例题讲解】
小亮探究出解题方法如下:
已知 , , 求的值.
, ,
【方法运用】
根据上面的解题思路与方法,解决下列问题:
(1)小亮发现,借助原题的条件还可以求出的值,请你帮助小亮完成解答过程;
(2)若 , . 则________,________;
【拓展提升】
(3)如图,点C是线段上的一点,以、为边向两边作正方形,已知 , 两正方形的面积和 , 直接写出图中阴影部分的面积S.

-
6、(1)试说明代数式的值与s、t的取值有无关系;
(2)已知多项式与的乘积展开式中不含x的一次项,且常数项为 , 试求的值.
-
7、如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化.

(1)求绿化的面积.(用含a、b的代数式表示)
(2)当a=2,b=4时,求绿化的面积.
-
8、如图,在中, , , F为延长线上一点,点在上,且 .
 (1)、求证:;(2)、若 , 求的度数.
(1)、求证:;(2)、若 , 求的度数. -
9、如图,在与中,点C在线段上,且 , , , . 求证: .

-
10、化简: .
-
11、计算: .
-
12、小明在做作业的时候,不小心把墨水滴到了作业本上的等式处,阴影部分即为被墨汁遮住的部分,那么被墨汁遮住的代数式是 .
-
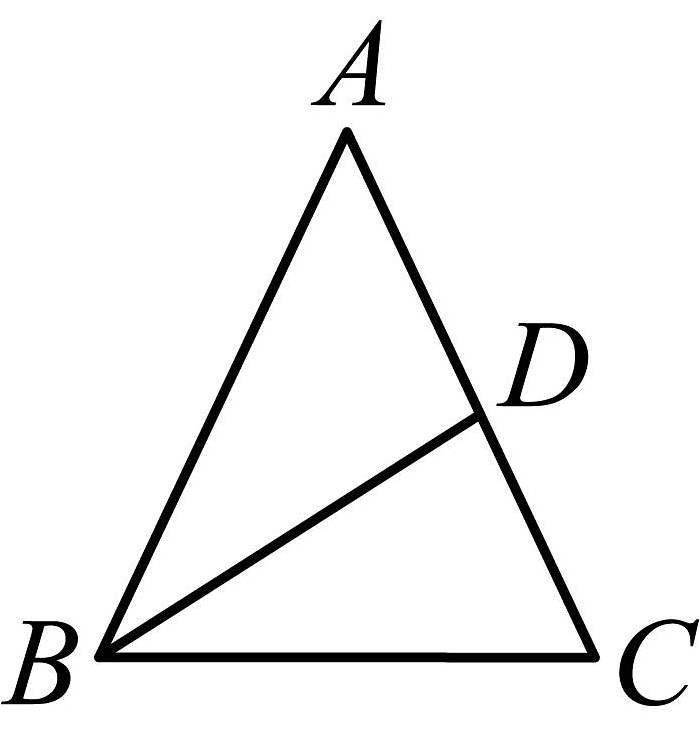
13、如图,中, , , 平分 , 则 .
-
14、如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是 .

-
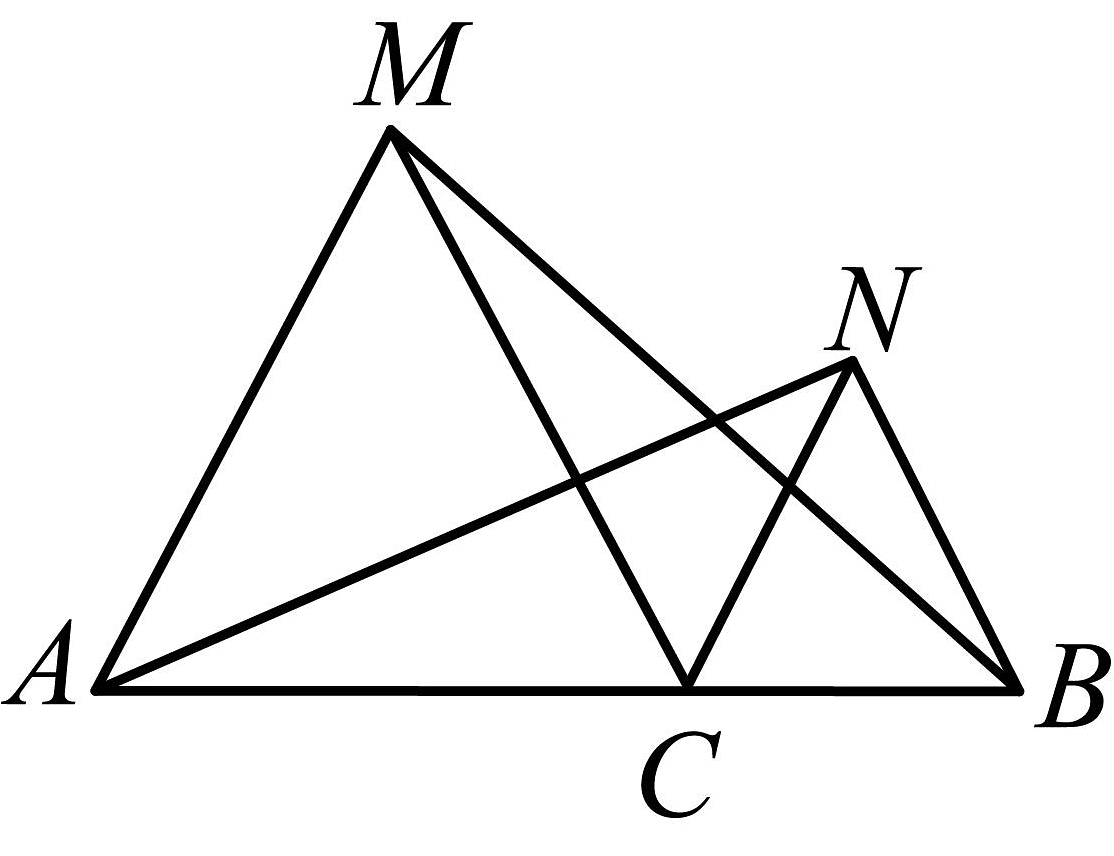
15、如图,在中,按下列步骤作图:①分别以B、C为圆心,以大于的长为半径作弧,两弧相交于两点M、N;②作直线交于点D,连接 . 若 , , 则的周长为( )
 A、7 B、9 C、11 D、13
A、7 B、9 C、11 D、13 -
16、如图,与都是等边三角形, , 若不动,将绕点C旋转,则在旋转过程中,与的大小关系是( )
 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定 -
17、如图,要测量池塘两岸相对的两点A、B间的距离,作线段与相交于点O,使 , , 只要测得C、D之间的距离,就可知道A、B间的距离,此方案依据的数学定理或基本事实是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、如图,在中,分别平分和 , 且相交于点O,若 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、(1)【问题解决】
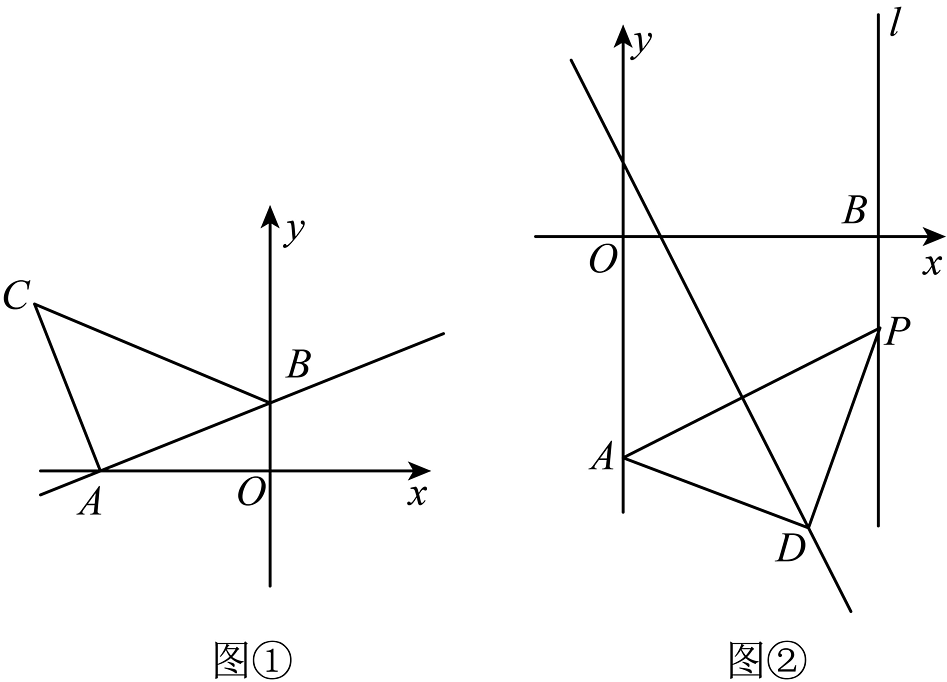
①如图①,在平面直角坐标系中,一次函数与x轴交于点A,与y轴交于点B,以为腰在第二象限作等腰直角 , , 点A,B的坐标分别为A__________,B__________.
②求①中点C的坐标.
小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点D.请借助小明的思路,求出点C的坐标;
(2)【类比探究】
数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图②,在平面直角坐标系中,点A坐标 , 点B坐标 , 过点B作x轴垂线l,点P是l上一动点,点D是一次函数图象上一动点,若是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标:______.
-
20、我们知道平方运算和开方运算是互逆运算 , 那么 . 那么如何将双重二次根式化简呢?如能找到两个数 , 使得 , 即 , 且使 , 即 , 那么 , 双重二次根式得以化简;
例如化简:;
∵且 ,
∴ ,
∴ .
由此对于任意一个二次根式只要可以将其化成的形式,且能找到使得 , 且 , 那么这个双重二次根式一定可以化简为一个二次根式.请通过阅读上述材料,完成下列问题:
(1)、填空:__________;__________;(2)、化简:①;② .