-
1、化简:(1)、;(2)、 .
-
2、计算:(1)、;(2)、 .
-
3、已知a、b表示两个有理数,规定一种新运算“*”为:a*b=2(a-b),那么5*(-2)的值为 .
-
4、若数轴上表示互为相反数的两点之间的距离是16,则这两个数的乘积是 .
-
5、化简: .
-
6、若单项式﹣2amb3与a5b2-n是同类项,则m﹣n=( )A、2 B、4 C、6 D、8
-
7、的运算结果是( )A、1.5 B、 C、 D、
-
8、下列说法正确的是( )A、单项式的次数是4 B、单项式的系数是 C、是整式 D、是四次三项式
-
9、冰箱保鲜室的温度零上记作 , 则冷冻室的温度零下记作( )A、 B、 C、 D、
-
10、如图,在数轴上,点表示的数可能是( )
 A、2.6 B、 C、1.8 D、
A、2.6 B、 C、1.8 D、 -
11、如图,已知抛物线y=﹣+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
 (1)、求A,B,C三点的坐标;(2)、若点P为线段BC上一点(不与B,C重合),轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;(3)、在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标.
(1)、求A,B,C三点的坐标;(2)、若点P为线段BC上一点(不与B,C重合),轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;(3)、在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标. -
12、如图,抛物线与y轴交于点 .
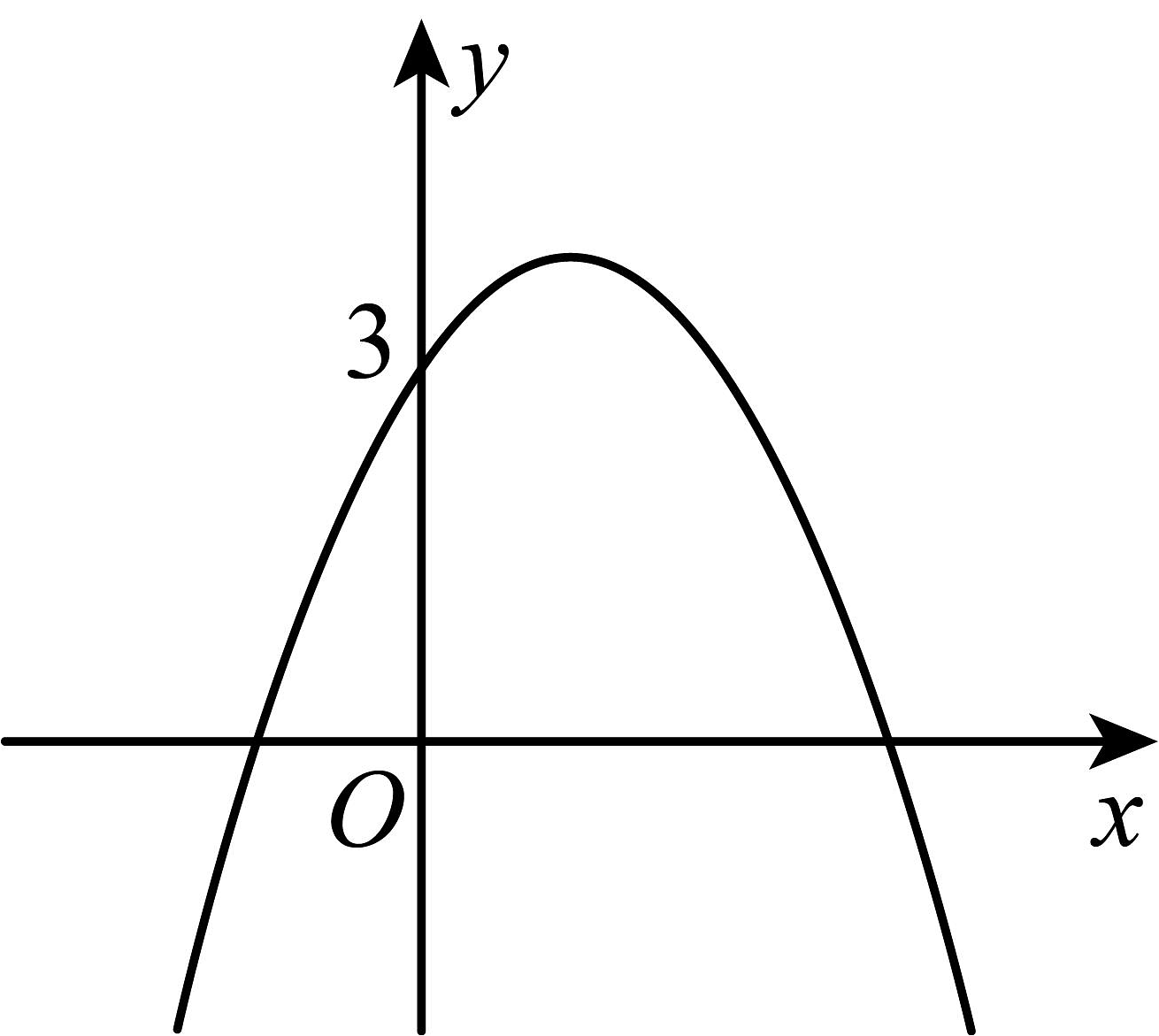 (1)、求出m的值及抛物线的解析式;(2)、求抛物线与x轴的交点和顶点坐标;(3)、当x取什么值时,抛物线在x轴上方?(4)、当x取什么值时,y的值随x的增大而减小?
(1)、求出m的值及抛物线的解析式;(2)、求抛物线与x轴的交点和顶点坐标;(3)、当x取什么值时,抛物线在x轴上方?(4)、当x取什么值时,y的值随x的增大而减小? -
13、已知二次函数 , 解答下列问题:(1)、用配方法求其图象的顶点坐标;(2)、填空:
①若点在其图象上,则线段的长为______;
②要使直线与该抛物线有两个交点,则b的取值范围是______.
-
14、如图,在正方形网络中,的三个顶点都在格点上,点A、B、C的坐标分别为、、 , 结合所给的平面直角坐标系解答下列问题:(1)、画出关于原点O对称的.(2)、平移 , 使点A移动到点 , 画出平移后的并写出点、的坐标.(3)、在、、中,与 成中心对称,其对称中心的坐标为 .

-
15、用适当的方法解下列方程:(1)、;(2)、 .
-
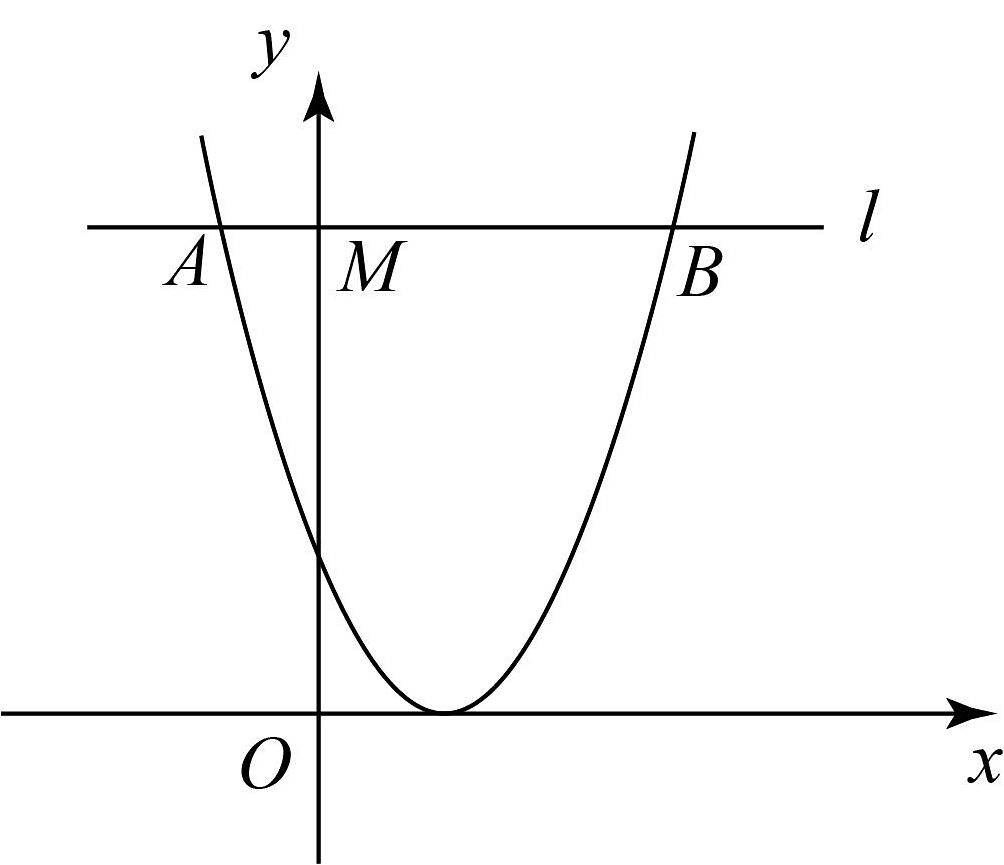
16、如图,抛物线y=x2+bx+c与x轴只有一个交点,与x轴平行的直线l交抛物线于A、B,交y轴于M,若AB=6,则OM的长为 .
-
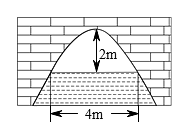
17、如图是抛物线型拱桥,当拱顶离水面时,水面宽 , 当水面宽度为时,水面下降了 .
-
18、下列两个电子数字成中心对称的是 . (填序号)

-
19、如图,二次函数的图象与轴的交点在与之间,对称轴为 , 函数最大值为4,结合图象给出下列结论:①;②;③;④若关于的一元二次方程有两个不相等的实数根,则;⑤当时,随的增大而减小.其中正确的结论有( )
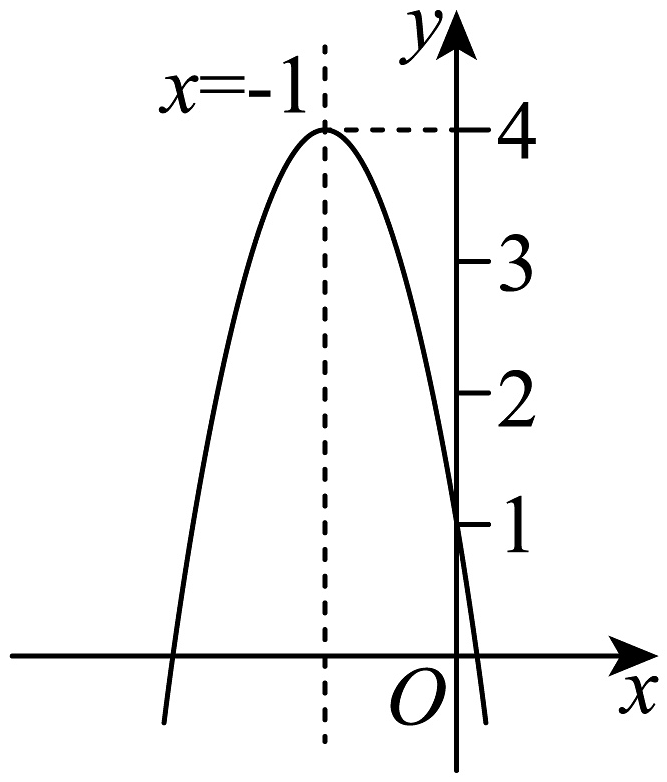 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个 -
20、如图,在中, , , 将绕点逆时针方向旋转得到 , 点恰好落在边上,连接 , 取的中点 , 连接 , 则的长是( )
 A、 B、 C、 D、
A、 B、 C、 D、