-
1、森林防火不仅是政府和相关部门的责任,每个公民应当参与到森林防火工作中去.如图所示,在一条笔直公路上,公路两旁是林地,位于森林防火卡点A的北偏东方向的B处发生火灾,防火员从卡点A去火灾处救援有两种方案.
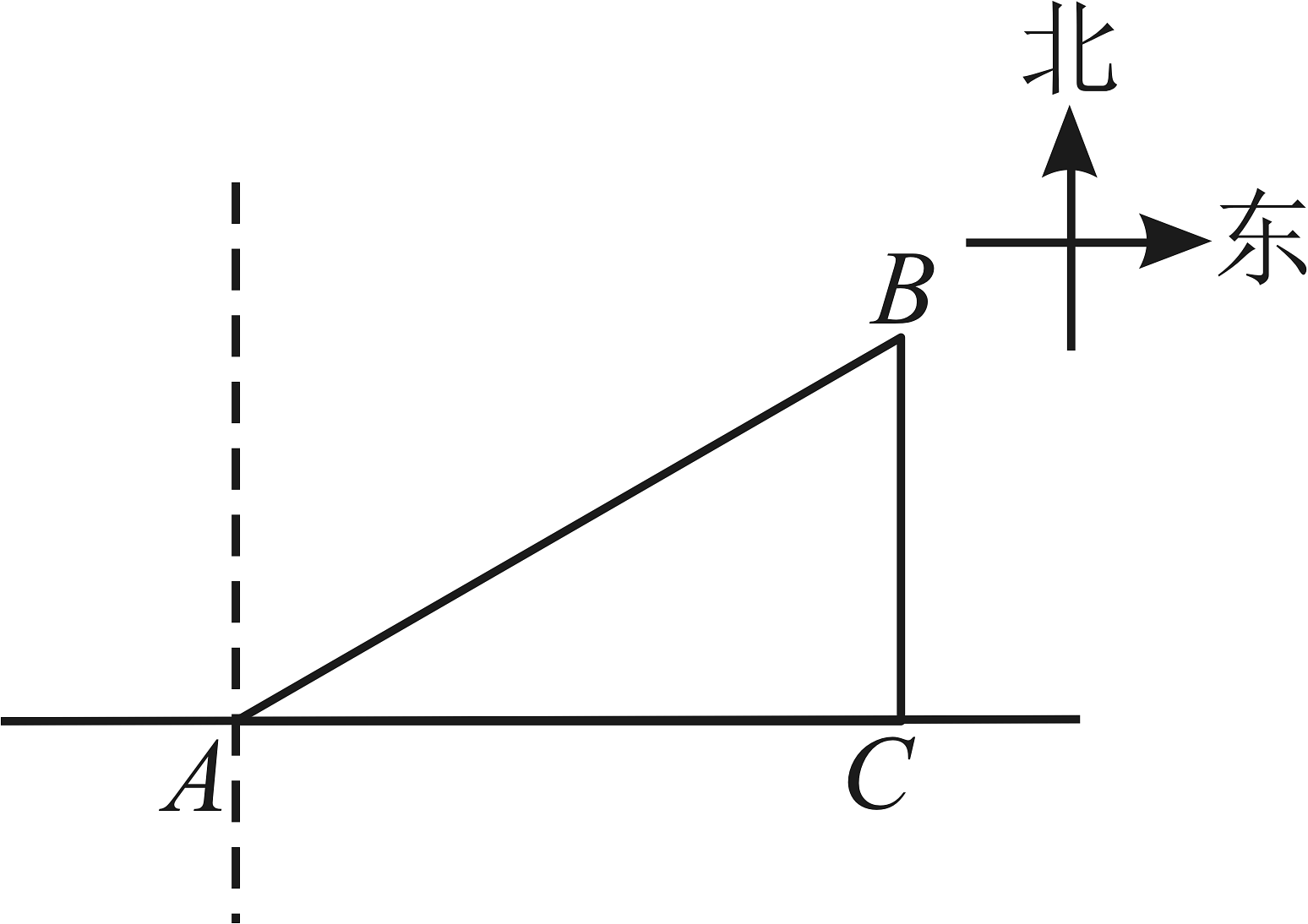
方案1:防火员立即骑车沿正东方向行驶800 m到达离B点最近的C处再跑步到B点救援;
方案2:防火员从卡点A直接跑步前往B处救援.若防火员的跑步速度 , 骑车的速度为 .
(1)、的长约为_____m(结果保留根号);(2)、防火员必须在两个方案中选择一个,请问选择哪个方案更合理,请通过计算说明理由. -
2、如图,在中, , D是边上一点,连接 , E,F分别为 , 的中点,连接 , , . 下面是两位同学的说法:
小星:根据题目条件,若添加条件 , 则可证明四边形是平行四边形.
小红:根据题目条件,若添加条件 , 则可证明四边形是平行四边形.
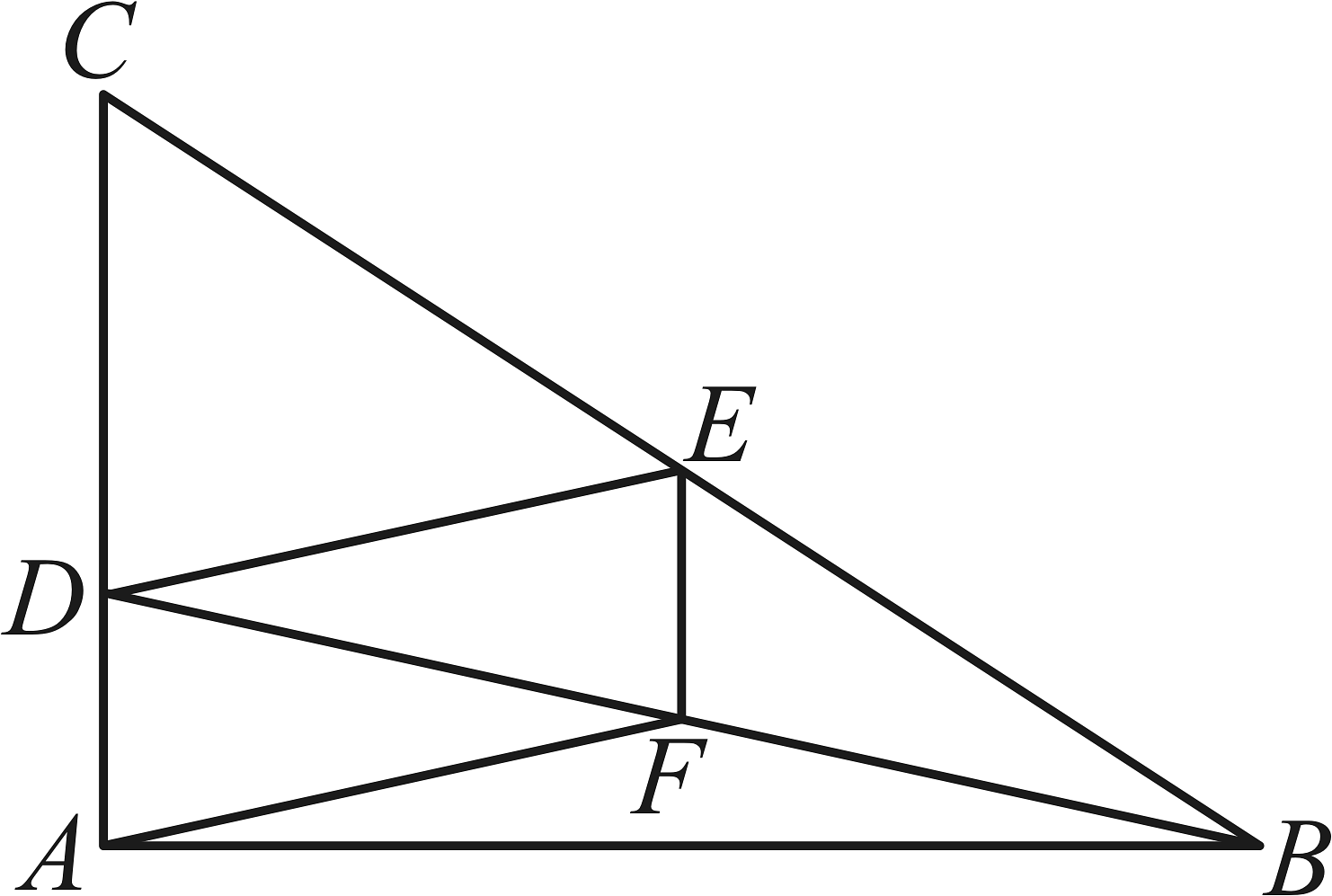 (1)、请你选择一位同学的说法,并进行证明;(2)、在(1)的结论下,若 , , 求的长.
(1)、请你选择一位同学的说法,并进行证明;(2)、在(1)的结论下,若 , , 求的长. -
3、(1)计算:;
(2)先化简,再求值: , 选择一个合适的整数m代入求值.
-
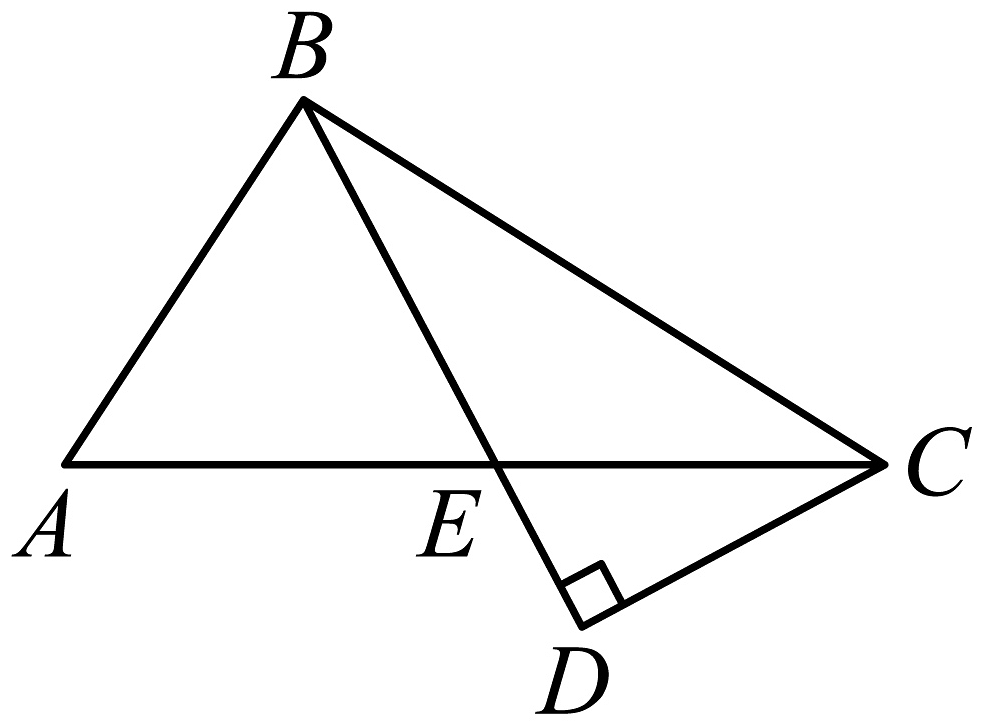
4、如图,在中, , 点E在边上, , , 交的延长线于点D,若 , 则的长为 .
-
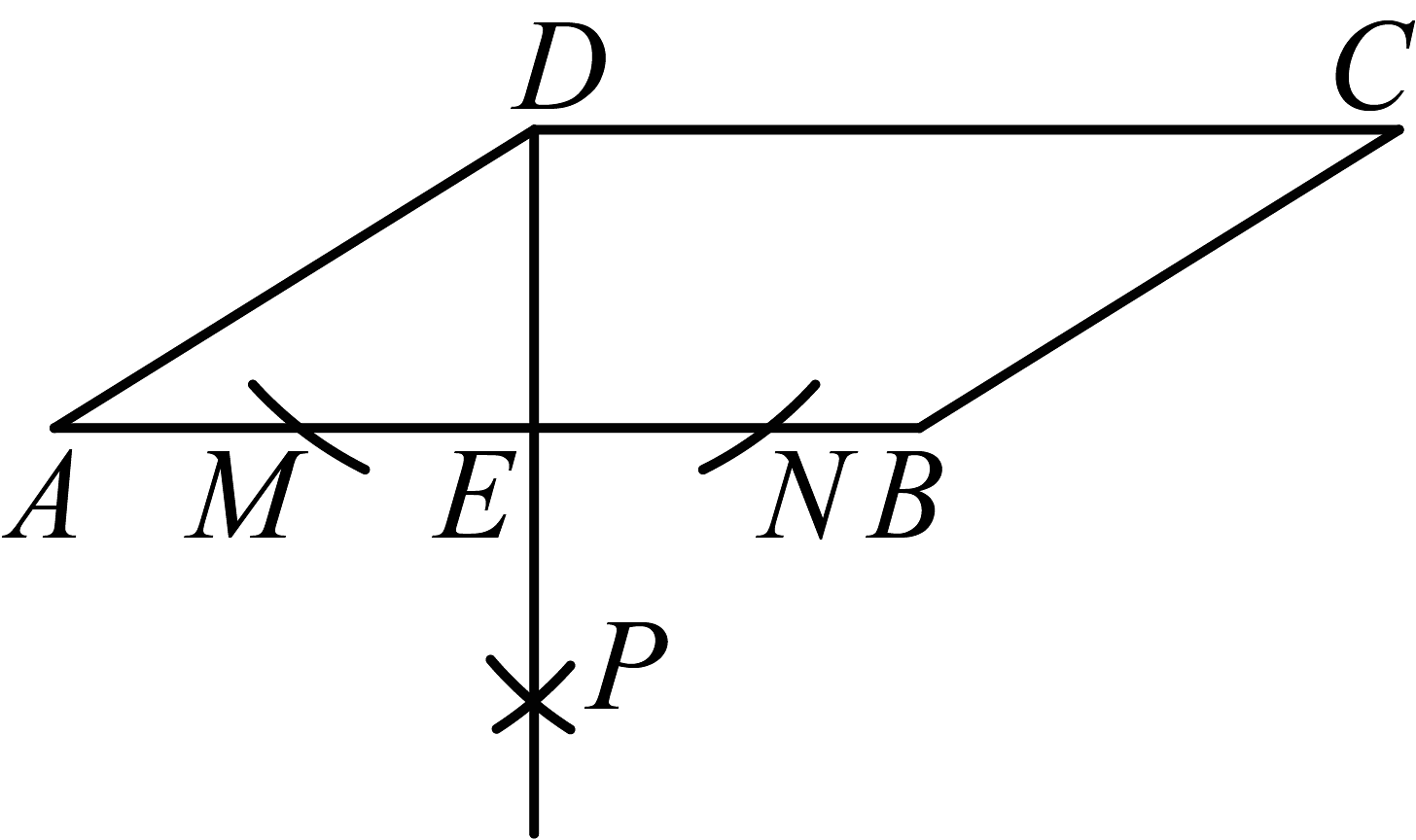
5、如图,在中,以点D为圆心,以一定长度为半径作弧,与边交于点M,N,再分别以点M,N为圆心,以大于的长为半径作弧,两弧交于点P,连接交于点E,若 , 则的长为 .
-
6、小红同学在做题的时候不小心将墨水滴到了作业本上恰好遮住了一个数字,得到一个不完整的方程 , 则被遮住的“?”代表的数字为 .
-
7、如图,抛物线与x轴交于点 , 其对称轴为直线 , 结合图象分析结论:①;②抛物线与x轴的另一个交点为;③;④ . 其中正确的结论有( )
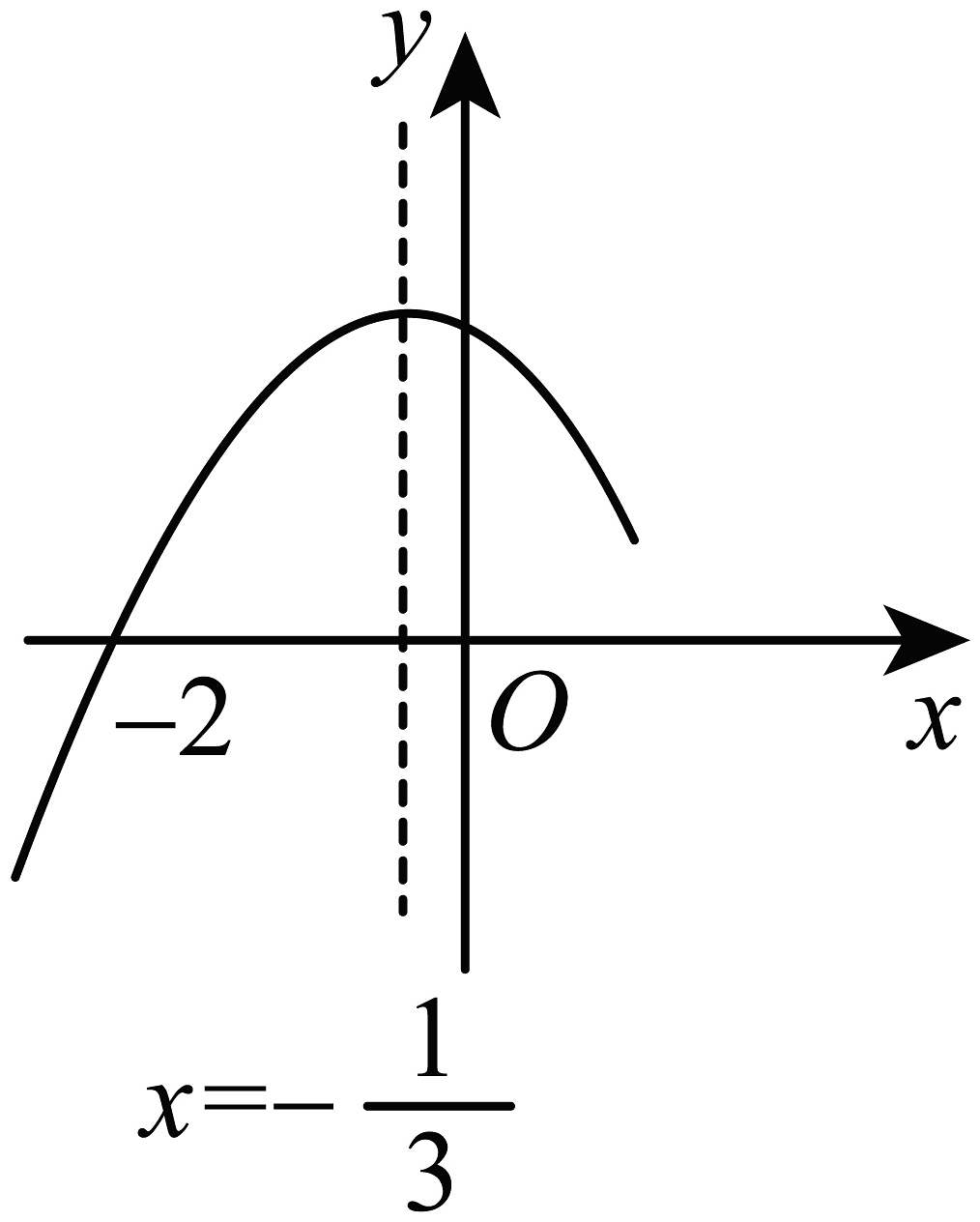 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
8、如图①是一块弘扬“新时代青年励志奋斗”的扇面宣传展板,该展板的部分示意图如图②所示,它是以点为圆心,长分别为半径,圆心角的扇面,若 , 则阴影部分的面积为( )
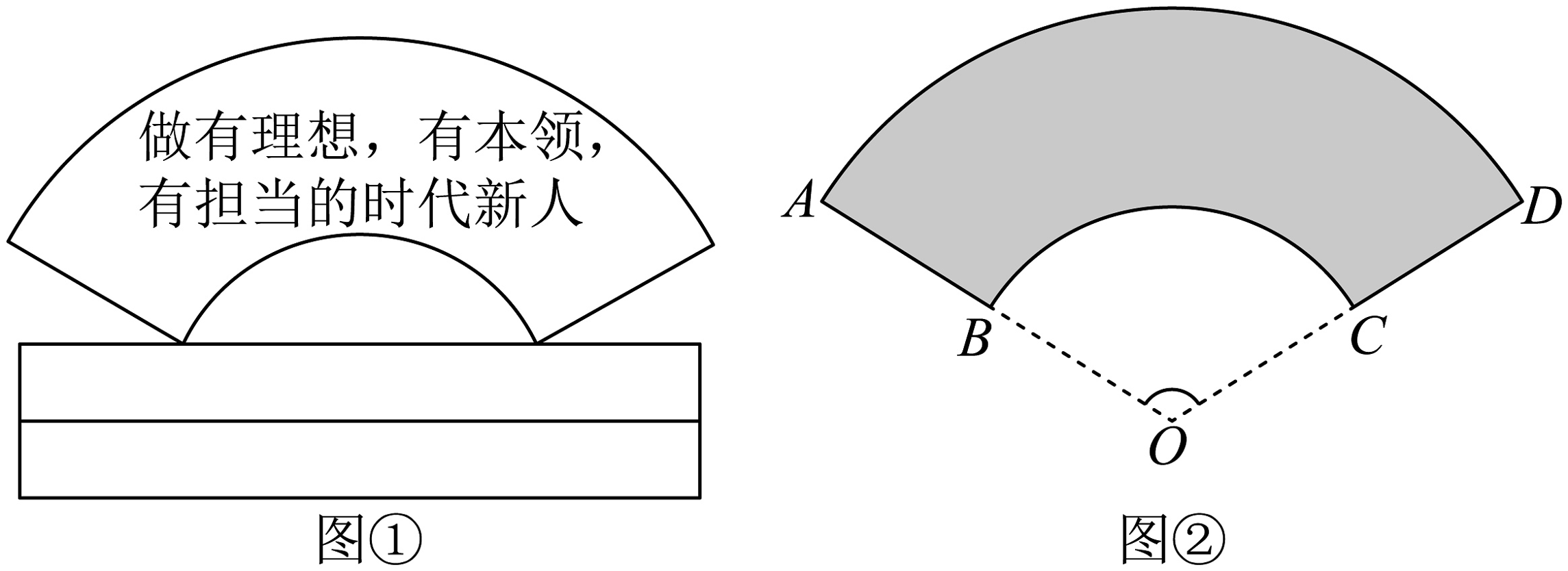 A、 B、 C、 D、
A、 B、 C、 D、 -
9、我国古代数学名著《九章算术》中有这样一道题:“今有善行者一百步,不善行者六十步,今不善行者先行一百步,善行者追之,问几何步及之?”大意为:“甲走路快,乙走路慢,两个人在相同时间里,甲走100步,乙走60步.现在乙先走100步,甲随后就追,甲要走多少步才能追上乙?设甲走了x步才追上乙,则下列方程正确的是( )A、 B、 C、 D、
-
10、已知一个不透明的箱子里有红球、黑球共六个,且小球除颜色外其余完全相同,若小明摸到红球的概率为 , 则黑球的数量为( )A、1个 B、2个 C、3个 D、4个
-
11、四名运动员参加了射击预选赛,他们测试成绩的平均数x及方差如下表所示:
甲
乙
丙
丁
8.4
9.2
9.2
8.5
1
1
1.1
1.7
如果选出一个成绩较好且状态稳定的人去复赛,那么应选( )
A、甲 B、乙 C、丙 D、丁 -
12、不等式的解集是( )A、 B、 C、 D、
-
13、一元二次方程的解是( )A、 , B、 , C、 , D、 ,
-
14、计算的结果正确的是( )A、 B、 C、 D、
-
15、下列是四个高校校徽的主体标识,其图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
16、如图,抛物线与x轴交于 , B两点,与y轴交于C点,对称轴直线 .
 (1)、求抛物线解析式;(2)、如图1,直线与抛物线,x轴分别交于点M,N,于点D,点E在坐标平面内,若以M,C,D,E为顶点的四边形是平行四边形,求点E的坐标;(3)、如图2,若过(2)中点D的直线与抛物线交于P、Q两点(点P在点Q左侧),过Q点的直线与抛物线交于点R,探究直线是否经过某个定点?若经过某定点,求该定点的坐标;若不经过定点,请说明理由.
(1)、求抛物线解析式;(2)、如图1,直线与抛物线,x轴分别交于点M,N,于点D,点E在坐标平面内,若以M,C,D,E为顶点的四边形是平行四边形,求点E的坐标;(3)、如图2,若过(2)中点D的直线与抛物线交于P、Q两点(点P在点Q左侧),过Q点的直线与抛物线交于点R,探究直线是否经过某个定点?若经过某定点,求该定点的坐标;若不经过定点,请说明理由. -
17、在正方形中,点E是上一动点(不与点B,C重合),连接 , 将绕点E顺时针方向旋转至位置,连接 , 交于点G.
 (1)、如图1,当点G为的中点时,若正方形的边长为4,求的长(2)、如图2,过点E作于点P,其延长线交于点Q.
(1)、如图1,当点G为的中点时,若正方形的边长为4,求的长(2)、如图2,过点E作于点P,其延长线交于点Q.①连接 , 求证:平分;
②当时,求的值.
-
18、如图,过点C作外接圆 , 的切线与的延长线交于点D,交于点 , 垂足为点 , 连接 .
 (1)、求证:是的切线;(2)、若 , , , 求的长.
(1)、求证:是的切线;(2)、若 , , , 求的长. -
19、如图,一次函数的图象与x轴交于点 , 与y轴交于点B,与反比例函数的图象在第一象限交于点 .
 (1)、求一次函数与反比例函数的表达式;(2)、D为第一象限反比例函数图象上的一动点,当的面积大于的面积时,直接写出点D的横坐标a的取值范围.
(1)、求一次函数与反比例函数的表达式;(2)、D为第一象限反比例函数图象上的一动点,当的面积大于的面积时,直接写出点D的横坐标a的取值范围. -
20、如图,中, , , 于 , 于 .
 (1)、求证: ,(2)、若 , , 求的长.
(1)、求证: ,(2)、若 , , 求的长.