-
1、【问题提出】小丽在上自主学习时,看到一个结论:对于任何一个封闭的平面图形,存在一条直线既平分周长,又平分面积.于是小丽利用初中所学知识进行初步验证.
【问题探究】
(1)小丽先选择了几个特殊图形进行验证,如图,请你在三个图形中任选两个,分别作一条直线,使这条直线既平分你所选图形的周长,又平分它的面积;
(2)如图,小丽在直角三角形中,作出一条直线 , 交于点E、交于点F,直线既平分的周长,又平分的面积.请根据小丽所给的数据计算:若 , , , , 用含有a的代数式表示 , 并求a的值;
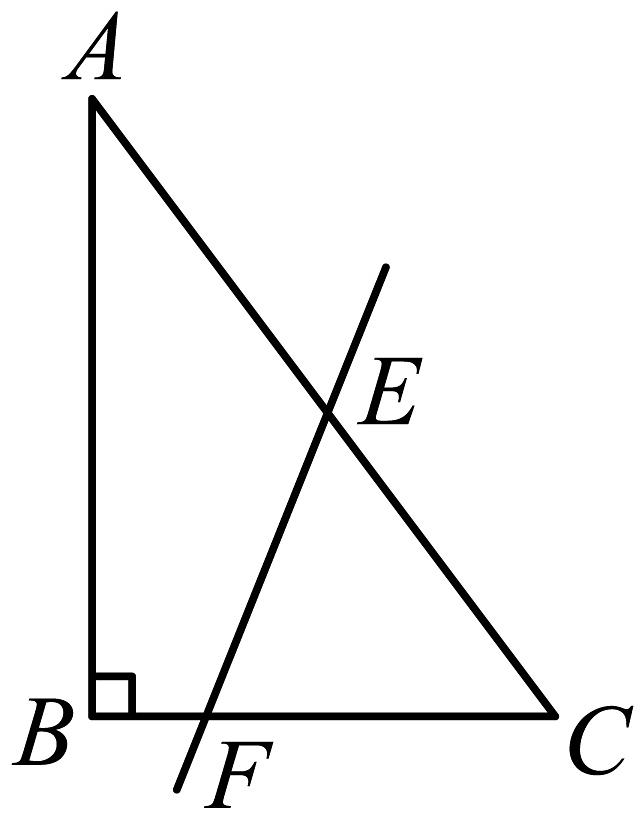
【问题解决】
(3)小丽家所在小区平面示意图如图,小区为方便居民出行,准备修一条笔直的道路(路宽不计),使这条道路所在的直线既平分四边形的周长,又平分四边形的面积.小丽利用所学知识进行思考,通过测量示意图得到 , , , , , . 若该道路的一个出口在边上,请帮小丽在图中画出这条直线,并在图中标出所有线段的长度.

-
2、某校为学生拍毕业照设计了一个拱门,该拱门的横截面由线段和一段抛物线构成,垂直于地面.将其截面放入平面直角坐标系如图1所示,点O为坐标原点,已知 , 抛物线顶点E的坐标为 .
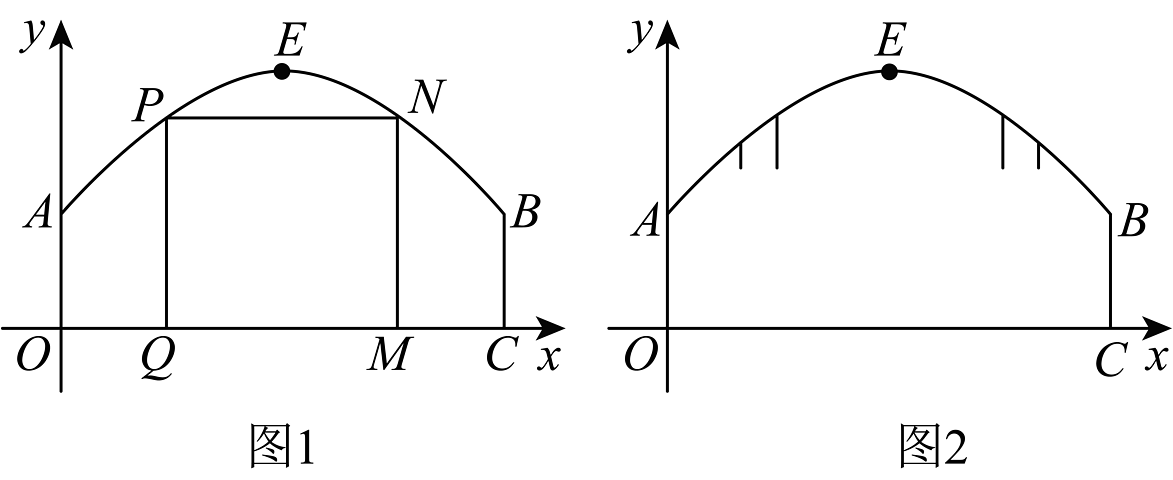 (1)、求拱门抛物线的函数关系式;(2)、现要在抛物线与地面围成的区域中用 , , 三根钢架隔出正方形区域供师生拍照留念,点P,N在抛物线上,点Q,M在地面上,求此正方形的边长;(3)、如图2,在拱门上安装彩灯,要求彩灯到地面的垂直距离为 , 每两个相邻彩灯之间的水平距离相等且不超过 , 左右外侧的两个彩灯安装在拱门的抛物线上.求至少需要安装彩灯的个数.(参考数据:)
(1)、求拱门抛物线的函数关系式;(2)、现要在抛物线与地面围成的区域中用 , , 三根钢架隔出正方形区域供师生拍照留念,点P,N在抛物线上,点Q,M在地面上,求此正方形的边长;(3)、如图2,在拱门上安装彩灯,要求彩灯到地面的垂直距离为 , 每两个相邻彩灯之间的水平距离相等且不超过 , 左右外侧的两个彩灯安装在拱门的抛物线上.求至少需要安装彩灯的个数.(参考数据:) -
3、如图,已知内接于 , 直径平分∠ACB,交于点D,交于点E,连接 .
 (1)、填空: (选填“<”、“>”或“=”);(2)、用尺规在图中作直线 , 使得直线与相切于点C;(保留作图痕迹,不写作法)(3)、判断与的位置关系,并说明理由.
(1)、填空: (选填“<”、“>”或“=”);(2)、用尺规在图中作直线 , 使得直线与相切于点C;(保留作图痕迹,不写作法)(3)、判断与的位置关系,并说明理由. -
4、沿河土家族自治县位于乌江下游,被称为“乌江百里画廊”.某数学兴趣小组借助无人机测量乌江某段河道的宽度.如图,在河岸边的点C处,兴趣小组控制一架无人机沿倾斜角的方向飞行到达点A处,然后无人机又沿垂直于河道的方向水平飞行至点B处,此时测得河对岸D处的倾斜角为 , 图中点A,B,D,C在同一平面内.
 (1)、求无人机从C飞到A时垂直上升的距离(结果保留根号);(2)、求该段河道的宽度(结果保留整数).(参考数据: , , , )
(1)、求无人机从C飞到A时垂直上升的距离(结果保留根号);(2)、求该段河道的宽度(结果保留整数).(参考数据: , , , ) -
5、贵州玉屏县被誉为“箫笛之乡”.玉屏县某中学举办“箫笛艺术节”活动,现需购买玉箫、玉笛若干支.已知玉萧单价比玉笛单价高10元,用1000元购买的玉萧数量与800元购买的玉笛数量相同.(1)、求玉萧和玉笛的单价各是多少元?(2)、学校计划购买玉箫与玉笛共30支,且玉箫的数量不少于玉笛数量的2倍,则学校最少需花费多少元?
-
6、2024年5月8日,云岩区中小学科学教育实验区建设正式启动,标志着我区在科学教育领域迈出了重要一步.某校为加强实验教学,确保每位学生都能动手操作、亲身体验,开设了七年级生物实验课,要求七年级学生每人在以下五个生物实验中选择一个进行研究(每人只选一个).
实验名称:
A.研究鱼游泳时鱼鳍的作用;
B.研究小鼠走迷宫的学习行为;
C.观察家蚕的完全变态发育过程;
D.观察青蛙的变态发育过程;
E.观察蚂蚁的信息交流.
为了解学生的选择情况,现从该校七年级随机抽取部分学生进行问卷调查,根据学生的选择,小红绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题:
 (1)、此次共调查学生 人;(2)、将条形统计图补充完整;生物实验D所在扇形的圆心角为 ;(3)、若该校七年级共有学生800人,请估计选择生物实验E的学生有多少人?
(1)、此次共调查学生 人;(2)、将条形统计图补充完整;生物实验D所在扇形的圆心角为 ;(3)、若该校七年级共有学生800人,请估计选择生物实验E的学生有多少人? -
7、如图,在中, , 点D,E分别是 , 的中点,连接 , 延长至点F,使 , 连接 .
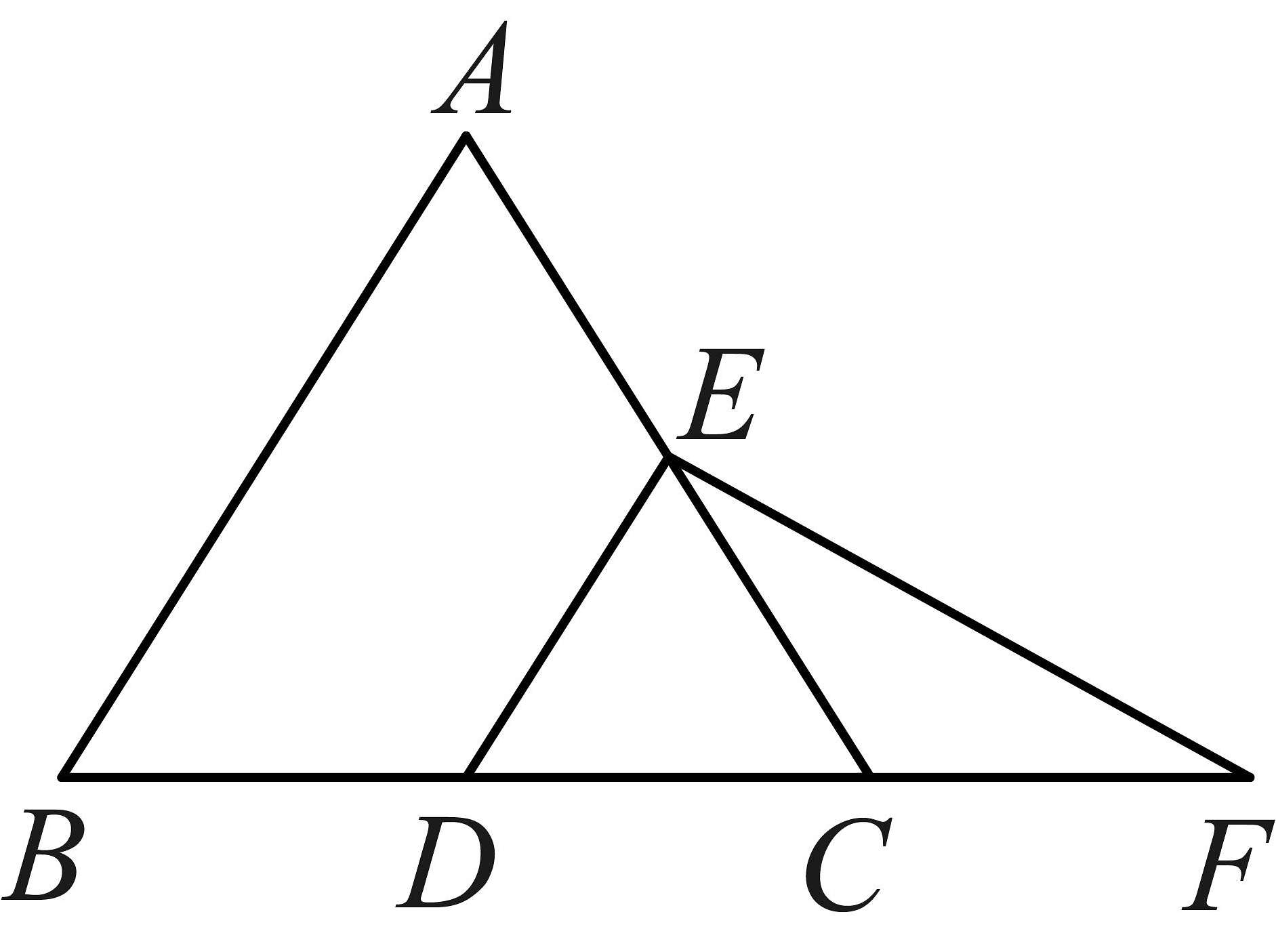 (1)、求证:是等腰三角形;(2)、已知 , 求的度数.
(1)、求证:是等腰三角形;(2)、已知 , 求的度数. -
8、
综合与实践:制作简易计时器
【问题情境】
某小组同学根据古代计时器“漏壶”的原理制作了如图所示的简易计时器,该计时器由一个圆锥和一个圆柱组成,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中.
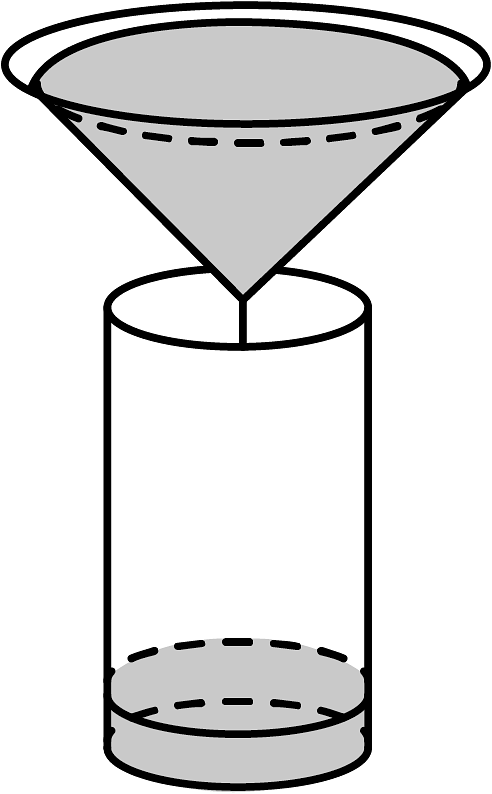
【实验观察】表格记录的是圆柱容器液面高度y()与时间x()的数据:
记录次数
第一次
第二次
第三次
第四次
第五次
时间x()
1
2
3
4
5
圆柱容器液面高度y()
2
4
6
4
10
【探索发现】根据上述的实践活动,该小组同学发现y与x之间满足一次函数关系,请解决以下问题:
(1)根据表中的数据在图中描点:小组长发现其中有一次数据记录错误,请你指出记录错误的是第 次:
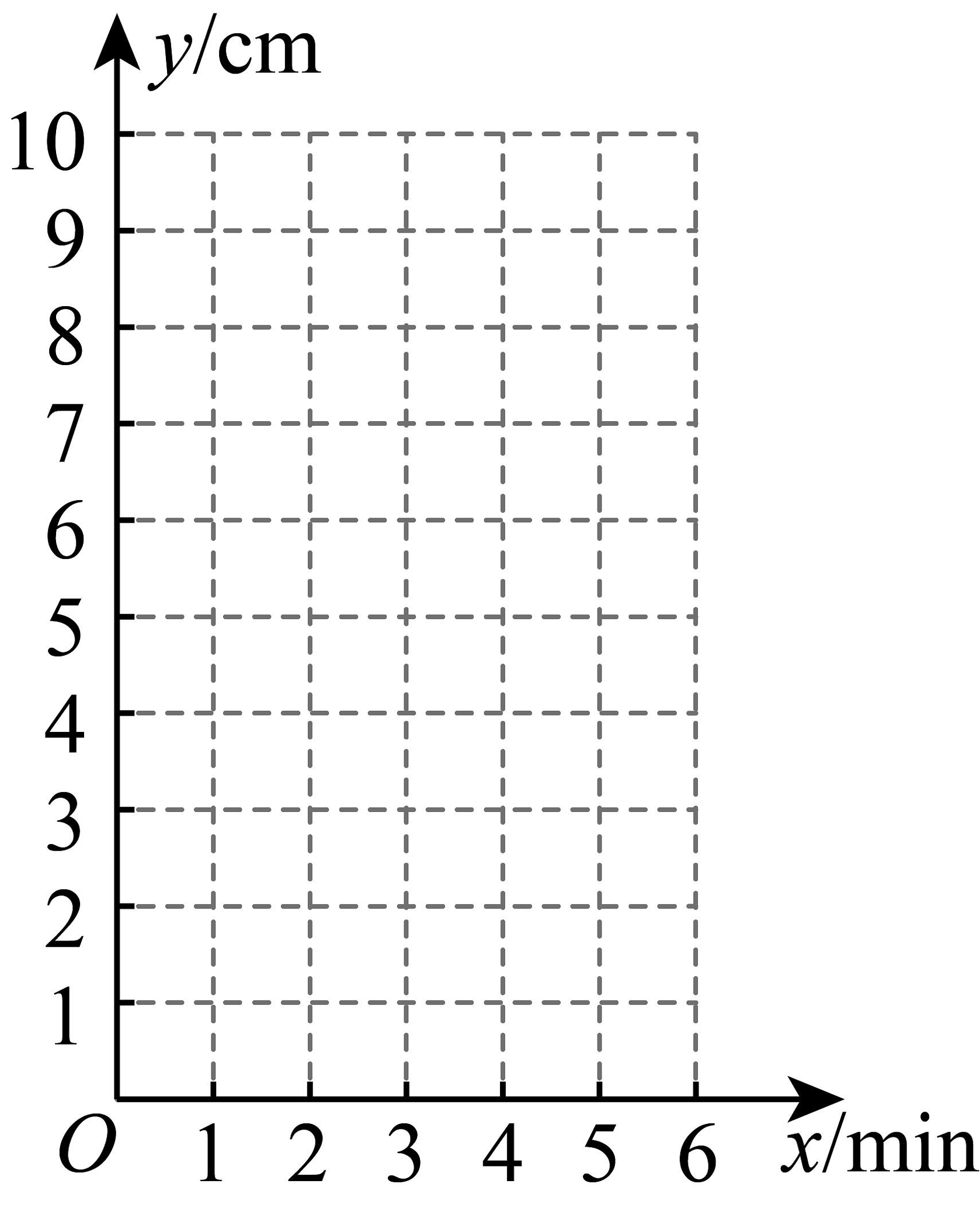
【结论应用】
(2)已知圆柱容器液面的最大高度能达到 , 则这个简易计时器最多可计时多少分钟?
-
9、(1)计算:;
(2)如图,数轴上的点A表示数 , 点B表示数 , 且点A始终在点B的左侧,求满足条件的x的取值范围.

-
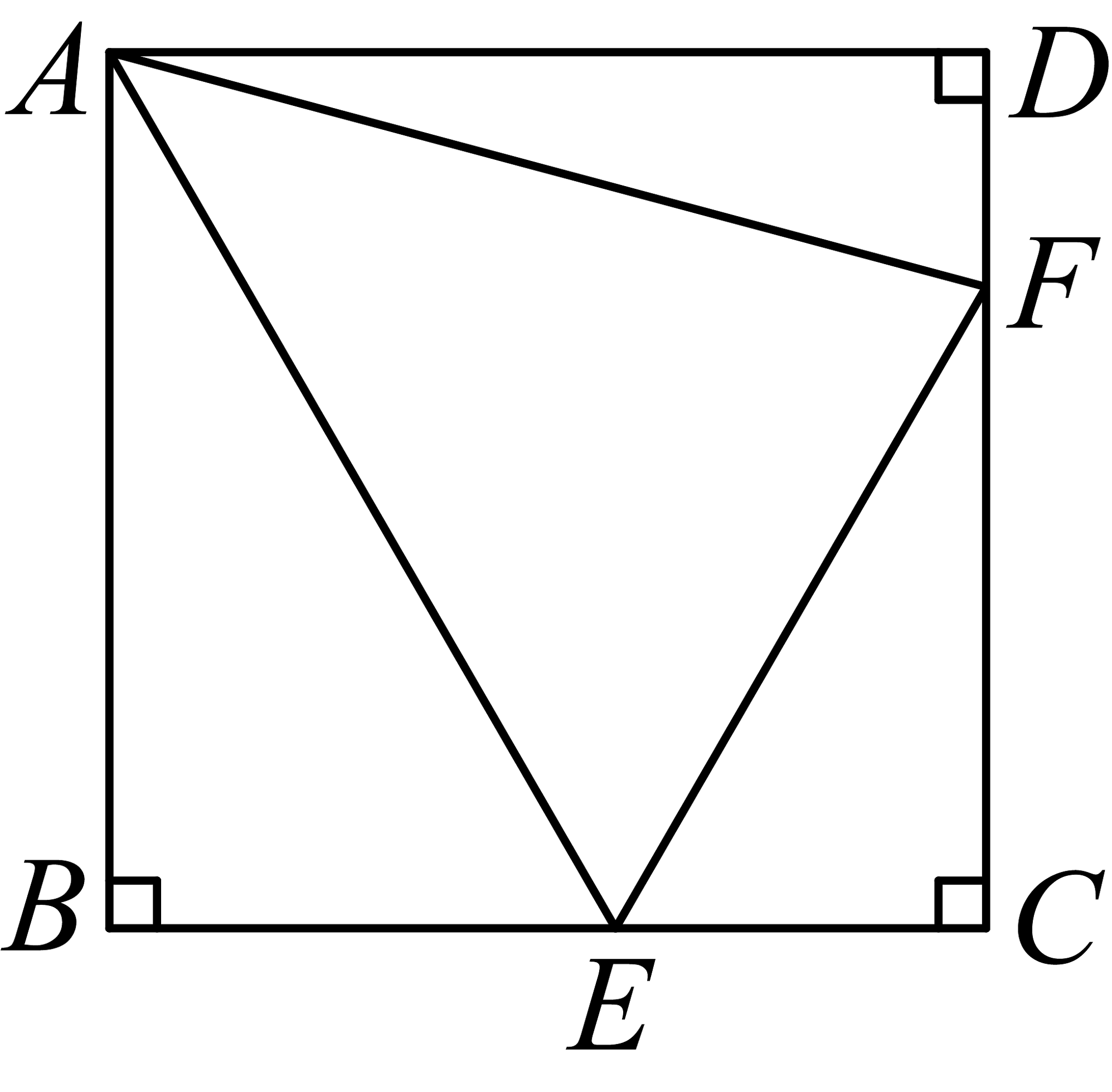
10、如图,中, , 的外角平分线交于点A,过点A分别作直线的垂线,B,D为垂足.已知 , 则的值为 .
-
11、若分式无意义,则x的值为 .
-
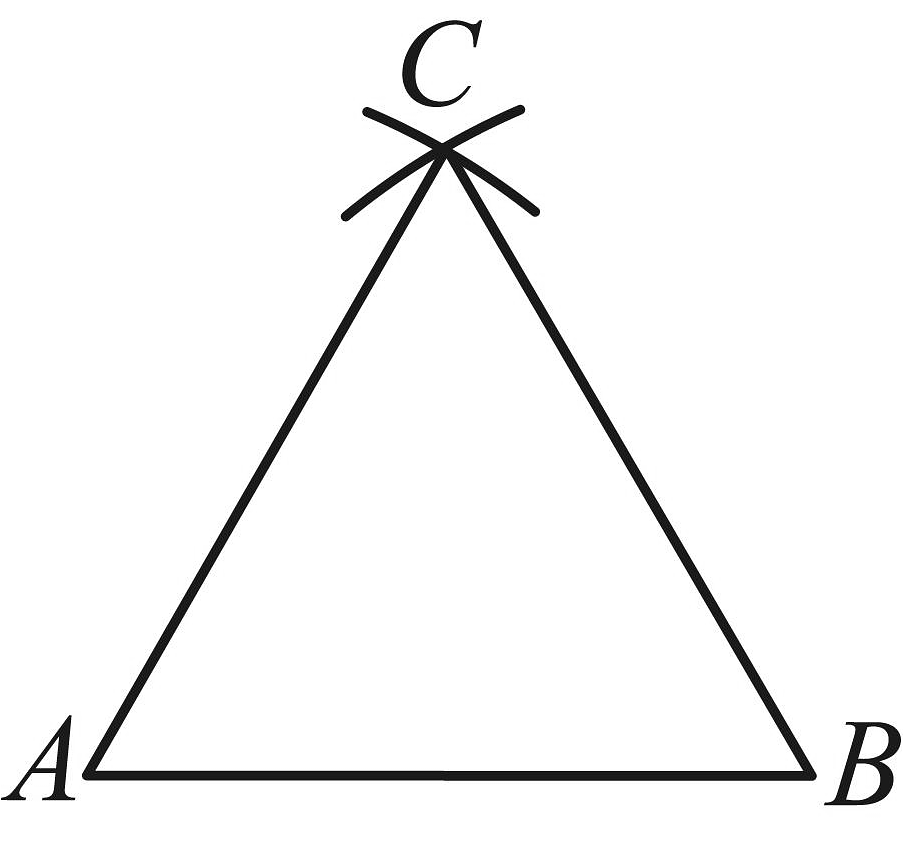
12、如图,已知线段 . 按下列步骤作图:①分别以点A,B为圆心、以的长为半径作弧,两弧交于点C;②连接 . 观察尺规作图的痕迹,的度数为 .
-
13、如图,在平面直角坐标系中,点在反比例函数(k为常数,)的图象上.将直线沿y轴向上平移后的直线与y轴交于点B,与此反比例函数的图象交于点C.若 , 则点B的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、中华美食讲究色香味美,优雅的摆盘能让美食锦上添花.图①外围的每一个拼盘的形状都是扇形的一部分,图②是其中一个的示意图(阴影部分为拼盘).测量得到 , , , 则图②所示的拼盘面积为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、根据表格中的信息,估计一元二次方程的一个解的范围是( )
x
0
1
2
5
A、 B、 C、 D、 -
16、一次函数(k,b为常数,)的图象如图所示,则关于x的不等式的解集为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、在剪纸活动中,小华想用一张矩形纸片剪出一个正八边形,如图,正八边形的一边与矩形的边重合,则的大小为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、甲、乙、丙、丁四名射击运动员各进行20次射击测试,他们的测试平均成绩相同,方差分别是 , , , , 则这四名射击运动员中成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁
-
19、用加减消元法解方程组时,将可得( )A、 B、 C、 D、
-
20、“加榜梯田”“从江鼓楼”“岜(bā)沙苗寨”是从江县著名旅游景点.以“从江鼓楼”为原点建立直角坐标系,若“岜沙苗寨”的坐标为 , 则“加榜梯田”的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、