-
1、将分别标有“多”“彩”“贵”“州”汉字的四个小球装在一个不透明的口袋中,这些小球除汉字外都相同,随机摸出一球,摸到标有“贵”字小球的概率是( )A、 B、 C、 D、
-
2、计算的结果是( )A、 B、 C、 D、
-
3、窗花是我国最具代表性的民间艺术之一.下列窗花图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
4、中国是最早采用正负数表示相反意义的量的国家.如果零上记作 , 那么零下记作( )A、 B、 C、 D、
-
5、在平面直角坐标系中,点O是坐标原点,抛物线(b是常数)经过点 , 点M在抛物线上,横坐标为m,点N的横坐标为 , 纵坐标与点M的纵坐标相同,点A在y轴上,纵坐标为m.当点M和点A的纵坐标不相等时,作点A关于点M的对称点B,作点A关于点N的对称点C,连结、、 .(1)、求该抛物线对应的函数表达式;(2)、试说明线段的长度为4;(3)、当直线与抛物线(b是常数)有两个交点时,设这两个交点分别为P、Q(点P在点Q左侧).
①若点M在对称轴左侧,点P在线段上,当此抛物线在内部(包括边)的点的纵坐标最大值与最小值的差为2时,求m的值;
②连结、 , 若点M在对称轴右侧,当时,直接写出m的值.
-
6、如图,在中, , , , 点在边上,连结 , 点是的中点,以为边作正方形 , 使点和点在直线同侧.
 (1)、求的面积;(2)、当时,求正方形的周长;(3)、当点落在上时,求的长;(4)、当点到直线的距离与点到直线的距离相等时,的长为 .
(1)、求的面积;(2)、当时,求正方形的周长;(3)、当点落在上时,求的长;(4)、当点到直线的距离与点到直线的距离相等时,的长为 . -
7、【问题原型】如图①,在中, , , . 点D是边上一点, , 连结 , 试探究线段长度的最小值.
【问题探究】如图②,小明发现点C的轨迹是以的中点为圆心,半径为3的圆的一部分,因为 , 所以点C的变化会导致点D的变化,于是将问题进一步转化为探究点D的轨迹问题:小明过点B作 , 使点E和点C在直线同侧,且 , 连结 , 则 , 可知恒为直角,又因为点B和点E均为定点,即可确定点D的轨迹.
以下是小明证明的部分过程:
证明:过点B作 , 使点E和点C在直线同侧,且 , 连结 .
证明过程缺失
……
又 , ,
,
.
请你补全缺失的证明过程.
【解决问题】在图③中,点O是线段的中点,请结合上述探究过程,用圆规和无刻度的直尺,在图③中作出【问题原型】中的点D,使线段长度的最小,此时线段长度的最小值是________.(保留作图痕迹)

-
8、电子体重秤的原理是当人站在秤盘上时,压力施加给传感器,传感器发生弹性形变,使阻抗发生变化,输出一个变化的模拟信号,将该信号进行处理并输出到显示器,显示出体重数据.某综合实践活动小组设计了简易电子体重秤:制作一个装有踏板(踏板质量忽略不计)的可变电阻R,与踏板上人的质量之间的几组对应值如表:
人的质量
0
30
60
90
120
可变电阻
240
180
120
60
0
 (1)、在平面直角坐标系中描出表中数据对应的点,根据点的分布规律,R与m符合初中学习过的某种函数关系,则可能是________函数关系(选填“一次”“二次”“反比例”) ;(2)、根据以上判断,当时,求R关于m的函数关系式;(3)、当可变电阻R为时,求人的质量m.
(1)、在平面直角坐标系中描出表中数据对应的点,根据点的分布规律,R与m符合初中学习过的某种函数关系,则可能是________函数关系(选填“一次”“二次”“反比例”) ;(2)、根据以上判断,当时,求R关于m的函数关系式;(3)、当可变电阻R为时,求人的质量m. -
9、为了了解学生体育锻炼的情况,某校对七年级部分学生每天体育锻炼的时间进行调查,并将收集到的数据进行整理、描述和分析.下面给出了部分信息:七年级部分学生每天体育锻炼时间的条形统计图及扇形统计图如下:(数据分成4组: , , , . 单位:小时)

根据以上信息,回答下列问题:
(1)、求C组人数,并补全条形统计图;(2)、若七年级学生每天体育锻炼的时间不低于1小时为达到标准,估计该校600名七年级学生体育锻炼时间达到标准的人数;(3)、下列结论一定正确的是________(填序号).①这组数据的中位数在范围内;
②B组数据在扇形统计图中所对应的圆心角为;
③根据题目中所给条件能求出这组数据的平均数.
-
10、图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
 (1)、在图①中,的顶点均为格点,在边上找到一点M,连接 , 使;(2)、在图②中,点A、B、O均为格点,过点B作的切线;(3)、在图③中,点A、B、O均为格点,在上找到点M和点N(点M和点N均不与点A重合),作 , 使 .
(1)、在图①中,的顶点均为格点,在边上找到一点M,连接 , 使;(2)、在图②中,点A、B、O均为格点,过点B作的切线;(3)、在图③中,点A、B、O均为格点,在上找到点M和点N(点M和点N均不与点A重合),作 , 使 . -
11、如图,在中, , 点D是延长线上一点, , 过点A和点D分别作 , 和相交于点E,连结 . 求证:四边形是矩形.

-
12、小明的爸爸要把一份文件通过快递公司送到与本市相距900千米的城市M,A公司的运输速度是B公司的1.5倍,选用A公司送此文件会比B公司早到5小时,求B公司的运输速度.
-
13、一个不透明的箱子里装有1个红色小球和3个白色小球,每个小球除颜色外其它完全相同.小亮从箱子里随机摸出一个小球,记下颜色后不放回箱子,然后小亮的爸爸又从箱子中随机摸出一个小球.用画树状图(或列表)的方法,求小亮和爸爸抽到同一颜色小球的概率.
-
14、先化简,再求值: , 其中 .
-
15、如图,在正方形中,点E和点F分别是边和的中点,连结、交于点G,点H是延长线上一点,连结 , 给出下面四个结论:①;②;③;④当时,;⑤当时, . 上述结论中,正确结论的序号有 .
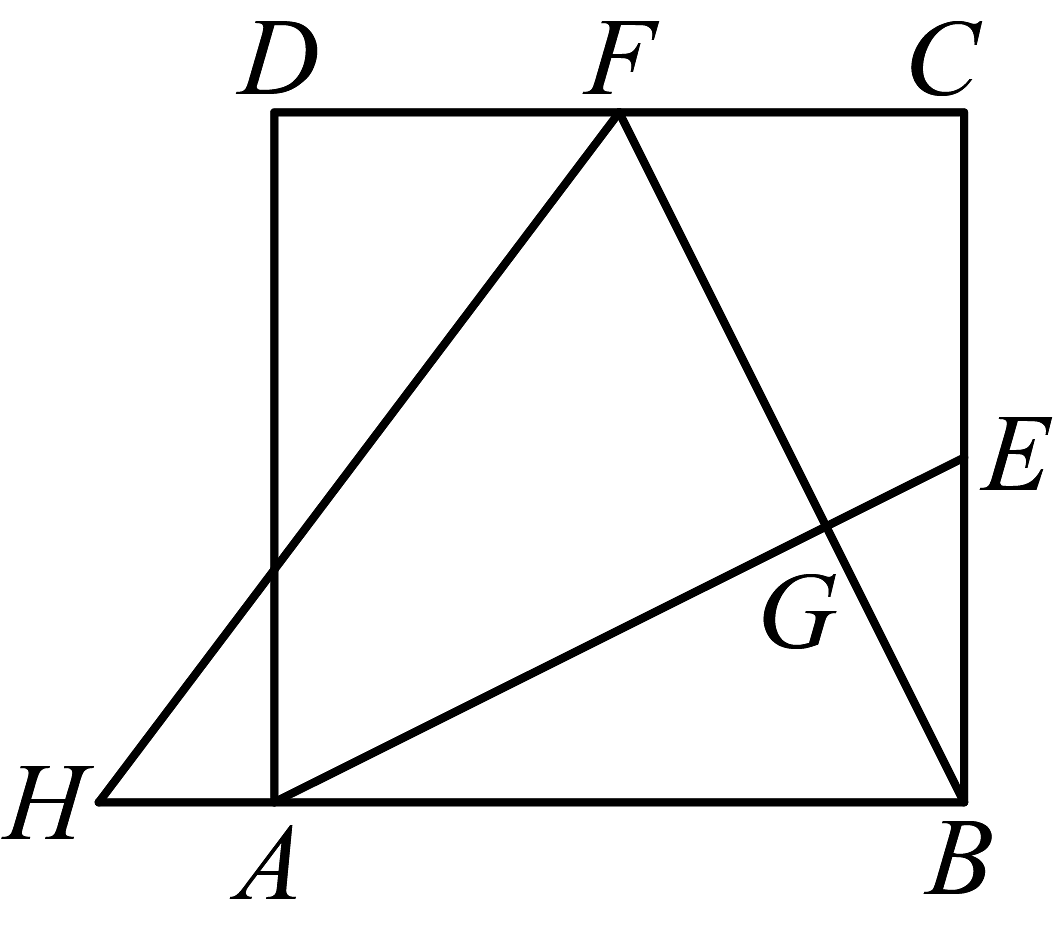
-
16、如图,在平面直角坐标系中,点O是坐标原点,直线分别交x轴、y轴于A、B两点,点P在线段上,与x轴交于M、O两点.若与直线相切,则线段的长度为 .

-
17、若一元二次方程有两个相等的实数根,则它的根是 .
-
18、比较大小:5(填“”“”或“”).
-
19、如图,在平面直角坐标系中,点O是坐标原点,点 , 是直线与双曲线的交点,线段及其下方的双曲线围成的封闭区域为G.图形G内(不含边界)的整点(横纵坐标都是整数的点)个数为( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个 -
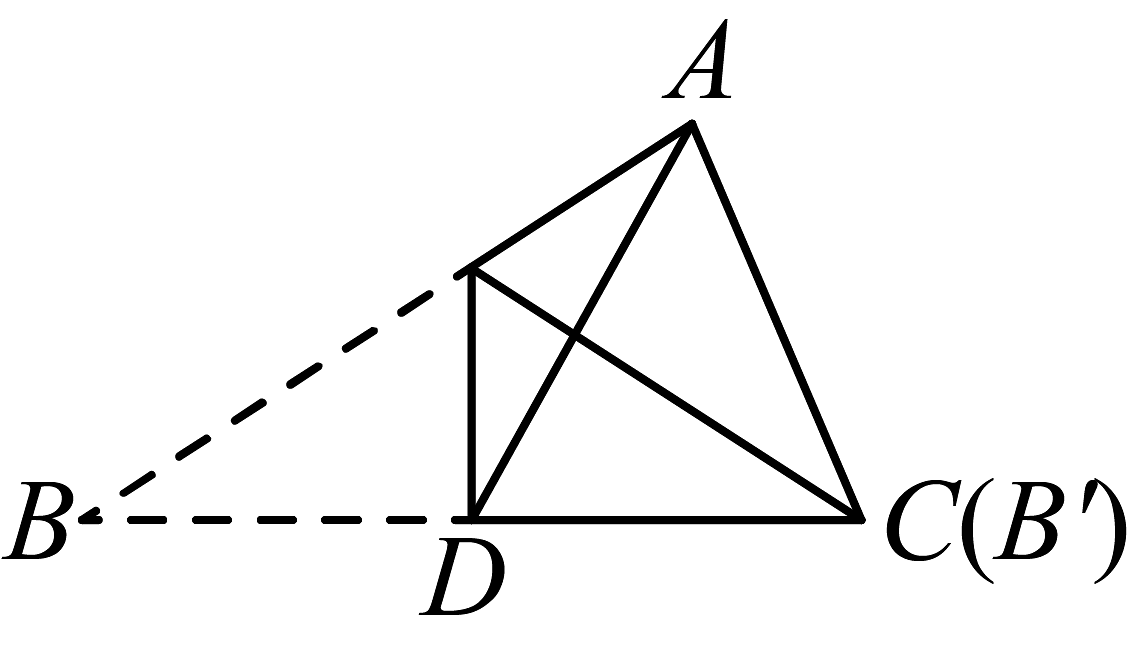
20、如图,根据下列图形折叠后的情况,可以判定是的角平分线的是( )A、
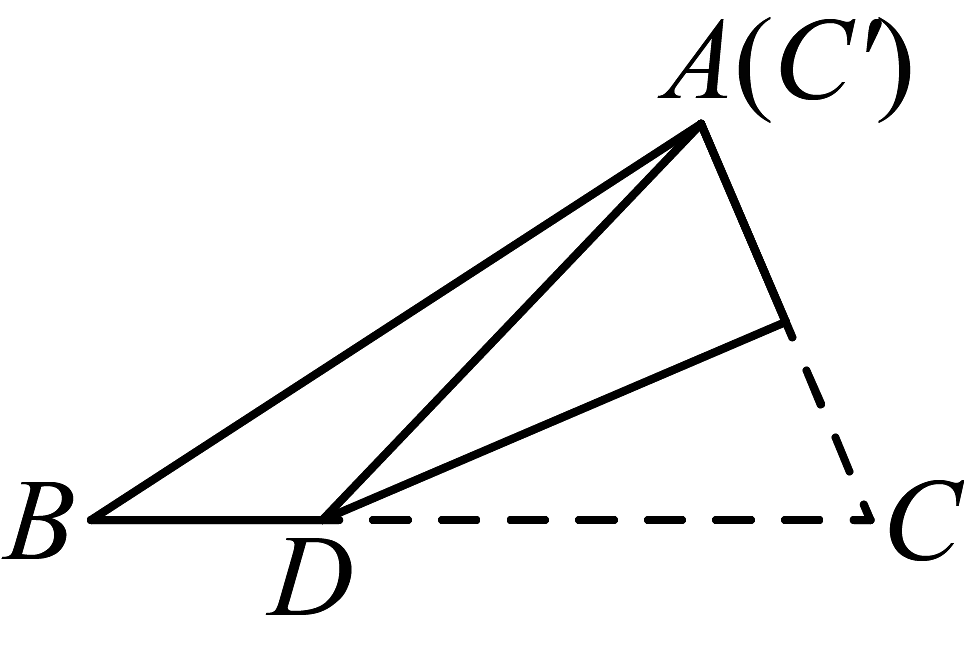 B、
B、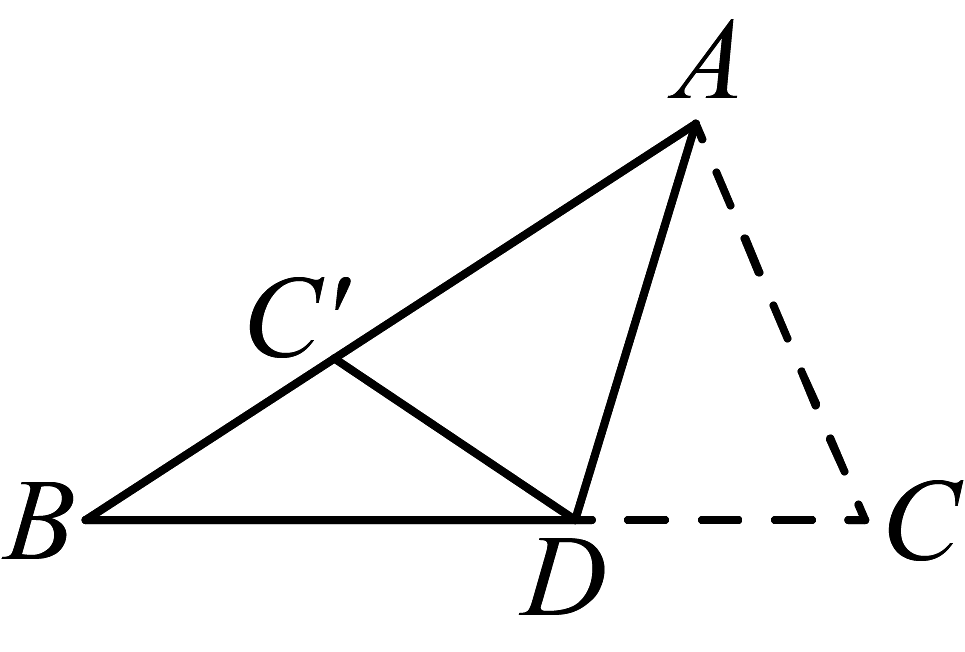 C、
C、 D、
D、