相关试卷

1、如图，在半径为3的扇形AOB中， $∠ A O B = 8 0^{°}$ ， C是弧AB上一点，连接OC，过点B作 $B D ⊥ O C$ ，垂足为D.若 $O D = D C$ ，则 $\overset{⌢}{A C}$ 的长为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{2}$ D、 $π$

查看解析
2、如图所示，线段AB是半圆O的直径，分别以点A和点O为圆心，大于 $\frac{1}{2}$ AO的长为半径作弧，两弧交于M，N两点，作直线MN，交半圆O于点C，交AB于点E，连结AC，BC，若AE=1，则BC的长是（）

A、2 $\sqrt{3}$ B、4 C、6 D、3 $\sqrt{2}$

查看解析
3、如图，AB是☉O的直径，CD为弦，CD⊥AB于点E，连结AC，AD，则下列结论中正确的是（）

A、 $\overset{⌢}{A C} = \overset{⌢}{B C}$ B、 $\overset{⌢}{B C} = \overset{⌢}{B D}$ C、OE=BE D、∠CAD=∠CDA

查看解析
4、已知一条弦把半径为8的圆分成1∶2的两条弧，则此弦的长为（）

A、4 $\sqrt{3}$ B、8 $\sqrt{3}$ C、8 D、16

查看解析
5、如图所示，在平面直角坐标系中，半径为2的☉P的圆心P的坐标为（-3，0)，将☉P沿x轴正方向平移，使☉P与y轴相切，则平移的距离为（）

A、1 B、1或5 C、3 D、5

查看解析
6、如图所示，已知四边形ABCD内接于☉O，∠ABC=70°，则∠ADC的度数为（）

A、70° B、110° C、130° D、140°

查看解析
7、已知的☉O半径为3cm，点P到圆心O的距离OP=2cm，则点P（）

A、在☉O外 B、在☉O上 C、在☉O内 D、无法确定

查看解析
8、已知实数a，b，c，m，n满足 $3 m + n = \frac{b}{a}$ ， $m n = \frac{c}{a}$ .

(1)、求证： $b^{2} - 12 a c$ 为非负数.

(2)、若a，b，c均为奇数，m，n是否可以都为整数？请说明你的理由.

查看解析
9、某种落地灯如图甲所示，AB为立杆，其高为84cm；BC为支杆，它可绕点B旋转，其中BC的长为54cm；DE为悬杆，滑动悬杆可调节CD的长度.支杆BC与悬杆DE之间的夹角∠BCD为60°.

(1)、如图乙所示，当支杆BC与地面垂直，且CD的长为50cm时，求灯泡悬挂点D距离地面的高度.

(2)、在如图乙所示的状态下，将支杆BC绕点B按顺时针方向旋转20°，同时调节CD的长（如图丙所示)，此时测得灯泡悬挂点D到地面的距离为90cm，求CD的长.（结果精确到1cm，参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84)

查看解析
10、如图所示，图甲和图乙是3×3的正方形网格，图丙是由圆和正方形网格组成的圆形，连结AB，AC，BC（点A，B，C均在格点上).请按要求完成下列作图：仅用无刻度直尺，且不能用直尺中的直角，保留作图痕迹.

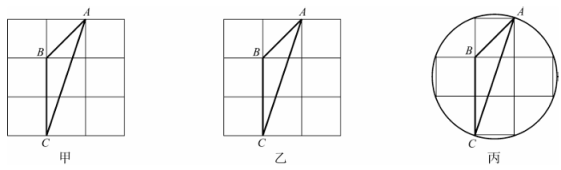(1)、在图甲中作出边AC上的中线.

(2)、在图乙中作出边AB上的高线.

(3)、在图丙中作出∠BAC的角平分线.

查看解析
11、如图所示，在矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在边AD上的点F处，过点F作FG∥CD，交BE于点G，连结CG.

(1)、求证：四边形CEFG是菱形.

(2)、若AB=6，AD=10，求四边形CEFG的面积.

查看解析
12、已知线段a，b，c满足 $\frac{a}{3} = \frac{b}{2} = \frac{c}{6}$ ，且 $a + 2 b + c = 26$ .

(1)、分别求线段a，b，c的长.

(2)、若线段x是线段a，b的比例中项线段，求线段x的长.

查看解析
13、如图，平面直角坐标系xOy中，矩形OABC的顶点B在函数y= $\frac{k}{x}$ （x>0)的图象上，A（1，0)，C（0，2).将线段AB沿x轴正方向平移得线段A'B'（点A平移后的对应点为A')，A'B'交函数y= $\frac{k}{x}$ （x>0)的图象于点D，过点D作DE⊥y轴于点E，则下列结论：
①k=2；
②△OBD的面积等于四边形ABDA'的面积；
③AE的最小值是 $\sqrt{2}$ ；
④∠B'BD=∠BB'O.
其中正确的结论有.（填写所有正确结论的序号)

查看解析
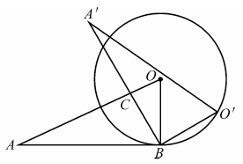
14、如图所示，☉O与△OAB的边AB相切，切点为B.将△OAB绕点B按顺时针方向旋转，得到△O'A'B'，使点O'落在☉O上，边A'B交线段AO于点C.若∠A'=25°，则∠OCB=度.

查看解析
15、已知A为直线y=-2x上一点，过点A作AB∥x轴，交双曲线y= $\frac{4}{x}$ 于点B.若点A与点B关于y轴对称，则点A的坐标为.

查看解析
16、在平面直角坐标系中，平行四边形ABCD的对称中心是坐标原点，顶点A，B的坐标分别是（-1，1)，（2，1)，将平行四边形ABCD沿x轴向右平移3个单位长度，则顶点C的对应点C₁的坐标是.

查看解析
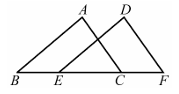
17、如图所示，△DEF是由△ABC通过平移得到，且点B，E，C，F在同一条直线上.若BF=14，EC=6，则BE的长是.

查看解析
18、如图所示，在Rt△OAB中，∠AOB=30°，将△OAB绕点O按逆时针方向旋转100°得到△OA₁B₁ ，则∠A₁OB的度数为.

查看解析
19、已知二次函数 $y = x^{2} - 2 a x + a (a \neq 0)$ 的图像经过 $A (\frac{a}{2}, y_{1}), B (3 a, y_{2})$ 两点，则下列判断中，正确的是（）

A、可以找到一个实数a，使得 $y_{1} > a$ B、无论实数a取什么值，都有 $y_{1} > a$ C、可以找到一个实数a，使得 $y_{2} < 0$ D、无论实数a取什么值，都有 $y_{2} < 0$

查看解析
20、欧几里得的《几何原本》中给出了一个找线段的黄金分割点的方法：如图所示，以线段AB为边作正方形ABCD，取AD的中点E，连结BE，延长DA至F，使得EF=BE，以AF为边作正方形AFGH，则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S₁ ，矩形BCIH的面积为S₂ ，则S₁与S₂的比值为（ )

A、 $\frac{\sqrt{5} + 1}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看解析

上一页 339 340 341 342 343 下一页跳转