相关试卷

1、已知一个矩形的长、宽分别为正整数a，b，其面积的数值等于它周长数值的2倍，则a+b=。

查看解析
2、有一个正在向上匀速移动的自动扶梯，旅客A从其顶端往下匀速行至其底端，共走了60级，B从其底端往上匀速行至其顶端，共走了30级(扶梯行驶，两人也在梯上行走，且每次只跨1级)，且A的速度(即单位时间所走的级数)是B的速度的3倍，那么自动扶梯露在外面的级数是。

查看解析
3、已知n是正整数，且n⁴-16n²+100是质数，那么n=。

查看解析
4、设正整数a，b，c，d满足条件 $\frac{a}{b} = \frac{b}{c} = \frac{c}{d} = \frac{5}{8}$ ，则 $a + b + c + d$ 的最小值是。

查看解析
5、在等边△ABC的边BC上任取一点D，作∠DAE=60°，AE交∠C的外角平分线于点E，那么△ADE是三角形。

查看解析
6、设a+b=1，a²+b²=2，那么a⁷+b⁷的值是。

查看解析
7、请你自己画图：画一个△ABC，三个顶点分别标上A，B，C，在BC边上任意取三个点(都不是B，C)，记为P，Q，R，在CA边上任意取两个点(都不是C，A)，记为M，N。连结线段AP，AQ，AR和BM，BN，这时你画的图中一共有个三角形。

查看解析
8、一直角三角形的两直角边长均为整数，且满足方程x²-(m+2)x+4m=0，试求m的值及此直角三角形的三边长。

查看解析
9、阅读材料，为解方程 $(x^{2} - 1)^{2} - 5 (x^{2} - 1) + 4 = 0$ ，我们可以将 $x^{2} - 1$ 看作一个整体，然后设 $x^{2} - 1 = y$ ①，那么原方程可化为 $y^{2} - 5 y + 4 = 0$ ，解得 $y_{1} = 1$ ， $y_{2} = 4$ 。当 $y_{1} = 1$ 时， $x^{2} - 1 = 1$ ，所以 $x^{2} = 2$ ，解得 $x = \pm \sqrt{2}$ ；当 $y_{2} = 4$ 时， $x^{2} - 1 = 4$ ，所以 $x^{2} = 5$ ，解得 $x = \pm \sqrt{5}$ 。故原方程的解为 $x_{1} = \sqrt{2}$ ， $x_{2} = - \sqrt{2}$ ， $x_{3} = \sqrt{5}$ ， $x_{4} = - \sqrt{5}$ 。
解答问题：

(1)、上述解题过程。在由原方程得到方程①的过程中，利用法解方程，体现了转化的数学思想；

(2)、请利用以上的知识解方程x⁴-x²-6=0。

查看解析
10、一般情况下： $\frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3}$ 不成立，但有些数可以使得它成立，例如： $a = b = 0$ 。我们称使得 $\frac{a}{2} + \frac{b}{3} = \frac{a + b}{2 + 3}$ 成立的一对数a， b为“相对数对”，记为（a，b）

(1)、若 $(1, b)$ 是“相对数对”，求b的值；

(2)、写出一个“相对数对”（a， b），并说明理由。（其中 $a \neq 0$ ，且 $a \neq 1$ ）

(3)、若（m， n）是“相对数对”，求代数式 $m - \frac{22}{3} n - [4 m - 2 (3 n - 1)]$ 的值。

查看解析
11、《希腊文选》中有这样一题：“驴和骡驮箱货物并排走在路上，驴子不停地埋怨驮的货物太重，压得受不了。骡子对它说：“你发什么牢骚啊！我驮的比你驮的更重，倘若你的货物给我一袋，我驮的货比你驮的货多1倍；而我若给你一口袋，咱俩才刚好一样多。”驴和骡各驮几口袋货物？”（请用方程组解答）

查看解析
12、如图，△ABC中，∠C=90°，AM=CM，MP⊥AB于点P。求证：BP²=BC²+AP²。

查看解析
13、若m适合关系式： $\sqrt{2 x + 3 y + 18 - m} - \sqrt{x + y - 116} = \sqrt{116 - x - y} - \sqrt{3 x + 2 y - m}$ ，求m的值。

查看解析
14、如果 $a + b + c = 0$ ， $\frac{1}{a + 1} + \frac{1}{b + 2} + \frac{1}{c + 3} = 0$ ，那么 $(a + 1)^{2} + (b + 2)^{2} + (c + 3)^{2}$ 的值为.

查看解析
15、如果一个多边形的边数增加1，它的内角和增加 $\frac{1}{10}$ ，则这个多边形的边数.

查看解析
16、已知 $\frac{x + y}{2} = \frac{z + y}{3} = \frac{x + z}{4}$ ，那么代数式 $\frac{x - 2 y + z}{2 x - y + z} =$ .

查看解析
17、如图，C、D是线段AB上两点，AC：BC=3：2，点D为AB的中点，AB=30。线段CD长是.

查看解析
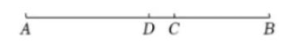
18、若nx²-x^m^-1+1=3是关于x的一元一次方程，则m= ， n=.

查看解析
19、我们知道 $\sqrt{3}$ 是无理数，而无理数是无限不循环小数，它的小数部分我们不可能全部地写出来，但是由于 $1 < \sqrt{3} < 2$ ，所以 $\sqrt{3}$ 的整数部分为1，小数部分为 $\sqrt{3} - 1$ 。根据以上的内容，解答下面的问题：若 $\sqrt{7}$ 的小数部分为a， $\sqrt{26}$ 的整数部分为b，则 $a + b - \sqrt{7}$ 的值是。

查看解析
20、如图，点A，B在数轴上表示的数分别为-2与+6，动点P从点A出发，沿A→B每秒2个单位长度的速度向终点B运动，同时，动点Q从点B出发，沿B→A以每秒4个单位长度的速度向终点A 运动，当一个点到达时，另一点也随之停止运动。那么当Q为AB的中点时，线段PQ的长是，当Q为PB的中点时，点P表示的数为。

查看解析

上一页 299 300 301 302 303 下一页跳转