-
1、(1)计算: .
(2)解不等式组 , 并把它的解集在数轴上表示出来.
-
2、如图,正方形网格中每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫做格点,已知的三个顶点都是格点,请按要求画出三角形.

(1)将先上平移1个单位长度再向右平移2个单位长度,得到;
(2)将绕格点O顺时针旋转 , 得到 .(1)、将先上平移1个单位长度再向右平移2个单位长度,得到;(2)、将绕格点O顺时针旋转 , 得到 . -
3、如图,一块面积为的三角形硬纸板(记为)平行于投影面时,在点光源O的照射下形成的投影是 , 若 , 则的面积是 .

-
4、如图,在平行四边形中,过对角线上一点P作 , , 且 , , 则四边形的面积是 .

-
5、如图,圆中两条弦相交于点E,其中两条劣弧的度数分别为 , 圆O的半径为5, , 则的长为 .

-
6、中,若 , , 则的最大值为 .
-
7、若一元二次方程的两个根分别为 , 则的值为 .
-
8、如图所示的零件的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
9、如图,矩形中, , 点P为上一动点(不与端点重合),连接 , 将沿折叠,点A落在点E处,连接 , 连接交于点F,交于点G,则下列结论正确的是( )
 A、若 , 则 B、若 , , 则的长为 C、若 , 则长度的最小值为1.8 D、和不可能全等
A、若 , 则 B、若 , , 则的长为 C、若 , 则长度的最小值为1.8 D、和不可能全等 -
10、在矩形中,是对角线上一点,连接并延长交于分别是的中点,连接 , 若 , 则的长度为( )
 A、 B、3 C、 D、
A、 B、3 C、 D、 -
11、如图,正方形和矩形的面积相等,反比例函数在第一象限的图象经过B、E两点,则的长为( )
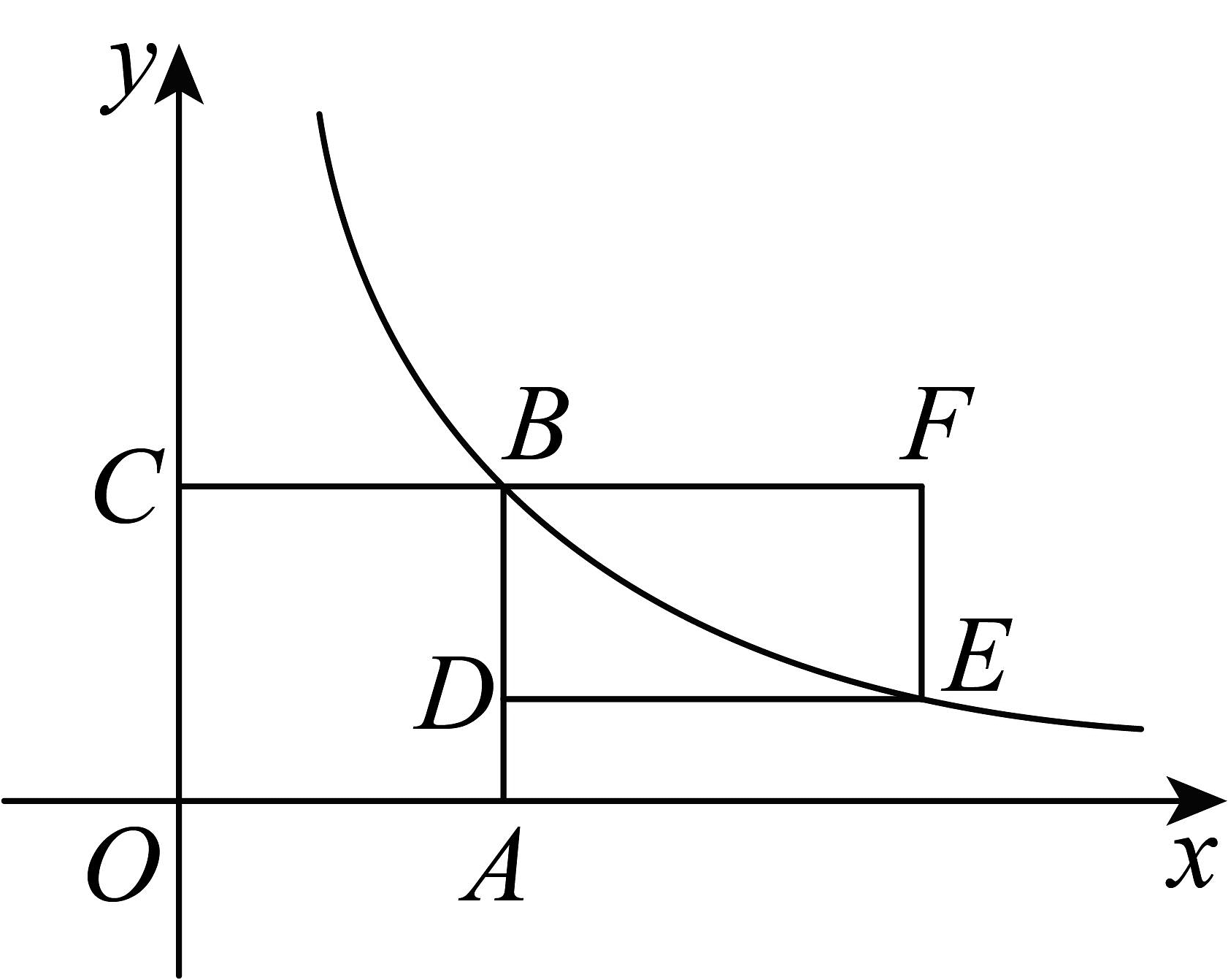 A、16 B、8 C、 D、
A、16 B、8 C、 D、 -
12、如图, 在中, 直径与弦相交于点 P, 连接 , , , 若 , , 则 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、如图,的三个顶点的坐标分别为、、 , 将绕C逆时针旋转后,A的对应点的坐标为( )
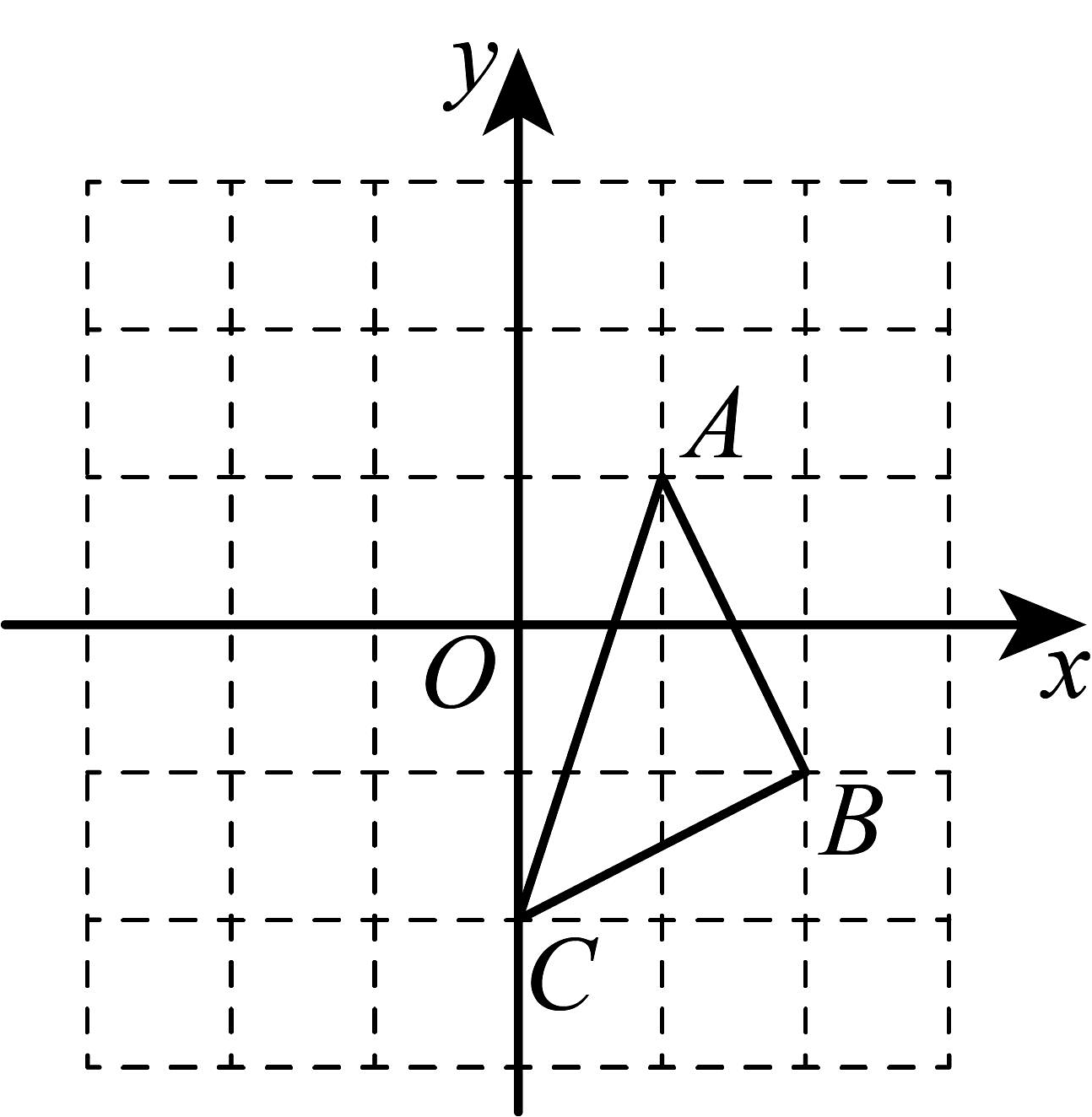 A、 B、 C、 D、
A、 B、 C、 D、 -
14、如图,已知开口向下的抛物线与轴交于点 , 对称轴为直线 . 则下列结论:①;②;③;④抛物线上有两点和 , 若且 , 则 . 其中正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
15、2025年1月18日,根据地区生产总值统一核算结果,2024年江西省地区生产总值为34202.5亿元,按不变价格计算,同比增长.34202.5亿可用科学记数法表示为( )A、 B、 C、 D、
-
16、在一次数学探究性学习活动中,某学习小组要制作一个圆锥体模型,操作规则是:在一块边长为16cm的正方形纸片上剪出一个扇形和一个圆,使得扇形围成圆锥的侧面时,圆恰好是该圆锥的底面.他们首先设计了如图所示的方案一,发现这种方案不可行,于是他们调整了扇形和圆的半径,设计了如图所示的方案二.(两个方案的图中,圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切)
(1)请说明方案一不可行的理由;
(2)判断方案二是否可行?若可行,请确定圆锥的母线长及其底面圆半径;若不可行,请说明理由.

-
17、如图1,果农正在进行的果树压枝处理可以减少树枝对营养成分的吸收,使更多的营养成分流向花芽,从而促进花芽分化,提高开花结果的数量和质量.如图2是一棵树枝在平面直角坐标系中的示意图,树枝近似呈直线生长,树枝上一点的生长高度与它到树干的水平距离近似满足一次函数关系 , 树枝经过压枝后变成抛物线形状,该抛物线最低点距离地面 , 且与树干的水平距离为 .
 (1)、求该抛物线的解析式(无需写出自变量的取值范围);(2)、经过压枝,树枝生长一段时间后依然满足(1)中的抛物线,且测得树枝端点处距离地面 . 为了使果树间不相互影响,要求树枝的最外端距离树干不得超过 , 试通过计算判断此树枝是否需要修剪.
(1)、求该抛物线的解析式(无需写出自变量的取值范围);(2)、经过压枝,树枝生长一段时间后依然满足(1)中的抛物线,且测得树枝端点处距离地面 . 为了使果树间不相互影响,要求树枝的最外端距离树干不得超过 , 试通过计算判断此树枝是否需要修剪. -
18、近来,由于的横空出世,大语言模型成为人工智能领域的热门话题.有关人员开展了、两款聊天机器人的使用满意度评分测验,并从中各随机抽取20份,对数据进行整理、描述和分析(评分分数用表示,分为四个等级:不满意 , 比较满意 , 满意 , 非常满意),下面给出了部分信息:抽取的对款聊天机器人的评分数据中“满意”的数据为84,86,86,87,88,89;抽取的对款聊天机器人的评分数据为65,68,69,81,84,85,86,87,87,88,88,94,95,96,96,96,98,98,99,100.

抽取的对、款聊天机器人的评分统计表
机器人
平均数
中位数
众数
“非常满意”所占百分比
88
96
88
88
根据以上信息,解答下列问题:
(1)、上述图表中________,________,________.(2)、根据以上数据,你认为哪款聊天机器人更受用户喜爱?请说明理由(写出一条理由即可).(3)、在此次测验中,有180人对款聊天机器人进行评分,240人对款聊天机器人进行评分,请估计此次测验中对聊天机器人不满意的人数. -
19、人间四月芳菲尽,山寺桃花始盛开.如图所示,点B为学校所在地,点D为歌乐山一寺庙,D点位于点B的北偏西方向.D点位于小雨家点A的北偏东方向.D点位于小瑜家点C的北偏西方向.又点A位于点B的正西方向,C点位于点B的正北方向,已知小雨家离学校的距离公里.(参考数据: , , )
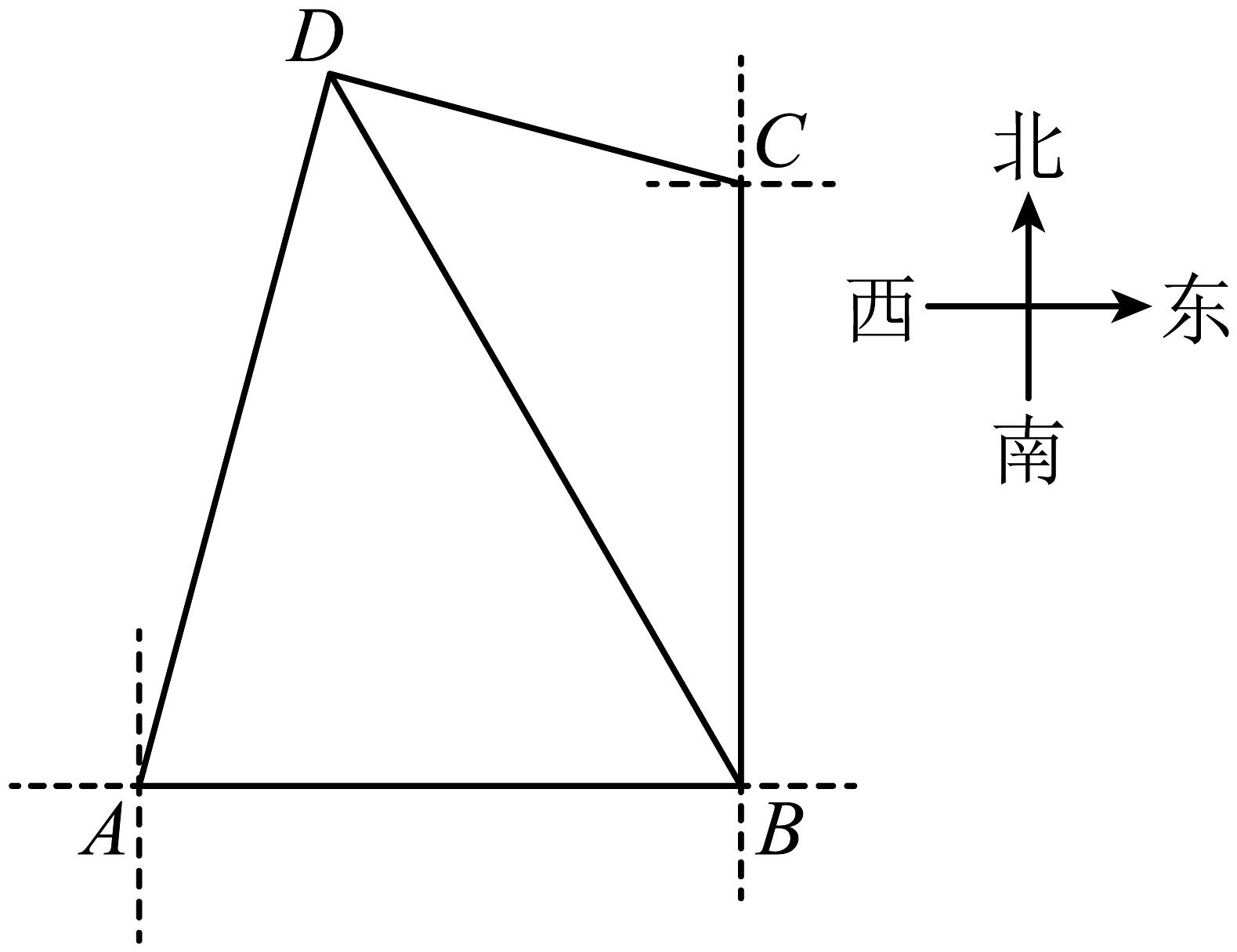 (1)、求小雨家A离寺庙D的距离(结果保留根号);(2)、甲、乙、丙三人邀约小雨和小瑜去寺庙D处看桃花,他们三人同时从学校出发,为了接A处的小雨,甲驾车以每小时60公里的速度从学校出发走路线① , 为了接C处的小瑜,乙驾车以每小时50公里的速度从学校出发走路线② , (接人时间忽略不计)丙骑共享电动自行车以每小时30公里的从学校出发走路线③ , 请通过计算说明,甲、乙、丙三人谁最晚达目的地D点?(结果精确到0.01)
(1)、求小雨家A离寺庙D的距离(结果保留根号);(2)、甲、乙、丙三人邀约小雨和小瑜去寺庙D处看桃花,他们三人同时从学校出发,为了接A处的小雨,甲驾车以每小时60公里的速度从学校出发走路线① , 为了接C处的小瑜,乙驾车以每小时50公里的速度从学校出发走路线② , (接人时间忽略不计)丙骑共享电动自行车以每小时30公里的从学校出发走路线③ , 请通过计算说明,甲、乙、丙三人谁最晚达目的地D点?(结果精确到0.01) -
20、请用直尺(无刻度)和圆规按下面要求作出符合条件的图形,不写作法但要求写出必要的文字说明(保留作图痕迹).
 (1)、如图1,在中, , , 在边上求作一点D,使得;(2)、如图2,在中,是钝角,在边的延长线上求作一点E,使得 .
(1)、如图1,在中, , , 在边上求作一点D,使得;(2)、如图2,在中,是钝角,在边的延长线上求作一点E,使得 .