相关试卷

1、项目式学习：圆弧在建筑中的应用

项目主题：圆弧在建筑中的应用
素材1	我国历史上著名的赵州桥，是现存世界上跨径最大、建造最早的单肩石拱桥，这是单圆弧设计在我国古代建筑中的一种成功典范．如图1，赵州桥主桥拱成圆弧形，跨度约37m ，拱高约7m ．
素材2	在西方建筑中，也有很多应用圆弧设计的元素．例如巴黎圣母院是典型的哥特式建筑．如图2，哥特式尖拱是由两段不同圆心的圆弧组成的对称图形，叫做两心尖拱．其中，点A、B称为起拱处，点C称为拱尖，C到AB的距离CD称为拱高．两心尖拱的几何特征就是 $\hat{A C}$ 、 $\hat{B C}$ 的圆心落在直线AB上．
素材3	如图3是古塔建筑中的方圆设计，寓意天圆地方．据古塔示意图，以塔底座宽AB为边作正方形ABCD（图4），塔高AF＝AC ，分别以点A ， B为圆心，AF为半径作圆弧，交于点G ．正方形ABCD内部由四个全等的直角三角形和一个小正方形组成．
问题解决
任务1	确定半径	（1）图1中赵州桥主桥拱半径R约为 m ．（结果保留整数）
任务2	计算拱高	（2）①请根据两心圆拱的几何特征利用尺规作出图2中 $\hat{A C}$ 、 $\hat{B C}$ 的圆心M、N ．（不写作法，保留作图痕迹）； ②在①的条件下，若MN＝2m ， AB＝3m ，求拱高CD ．
任务3	计算比值	（3）如图4，若点G落在AM的延长线上，连接GP交DQ于点T ，则 $\frac{G T}{G P}$ 的值为．

查看解析

2、“滨滨”和“妮妮”是2025年第九届亚洲冬季运动会的吉祥物．某亚冬会官方特许商品零售店购进了一批同一型号的“滨滨”和“妮妮”手办，连续两个月的销售情况如表：
月份
销售量/个
销售额/元
滨滨
妮妮
1月
80
50
6800
2月
100
60
8400

(1)、求该店“滨滨”和“妮妮”手办的单价；

(2)、为了扩大销量，增加盈利，该店对两种手办进行降价促销，其中“滨滨”手办八折销售，“妮妮”手办七五折销售，某学校欲购买若干个“滨滨”和“妮妮”手办作为亚冬会知识竞赛活动的奖品，且“滨滨”手办的数量恰好是“妮妮”手办数量的2倍，若总费用不超过1300元，那么该校最多可购买多少个“滨滨”手办？

查看解析
3、青少年是祖国的未来，民族的希望，有效保护、积极促进青少年身心健康成长十分重要．某校为了了解九年级学生的身体健康情况，从九年级随机抽取了若干名学生，测量他们的体重（均取整数，单位：kg），并将他们的体重进行整理，绘制了如下统计表与统计图：
组别
体重（kg）
频数（人）
A
39.5～46.5
2
B
46.5～53.5
a
C
53.5～60.5
8
D
60.5～67.5
5
E
67.5～74.5
4
已知C组的具体体重为（单位：kg）：54，54，55，55，56，57，59，60
根据以上信息，回答下列问题：

(1)、填空：a＝ ▲ ，所抽取学生体重的中位数是 ▲ ；

(2)、所抽取学生平均体重为58.8kg ，小敏的体重是57kg小敏推测自己的体重在所抽取的学生中处于中下游水平，请问小敏的推测正确吗？请简单说明理由．

(3)、如果该校九年级有600名学生，请估算九年级体重高于60.5kg的学生大约有多少人？

查看解析
4、先化简，再求值： $(\frac{a^{2} - 1}{a^{2} + 2 a + 1} - \frac{a}{a^{2} - a}) \div \frac{a - 2}{a + 1}$ ，其中 $a + \frac{1}{a} = 3$ ．

查看解析
5、计算： $\sqrt[3]{8} + | 3 - \sqrt{12} | + (\frac{π}{2} - 1.57)^{0} - 2 c o s 30 °$ ．

查看解析
6、如图，在▱ABCD中，∠B＝135°，AB $= \sqrt{2}$ BC ，将△ABC沿对角线AC翻折至△EAC ， AE与CD相交于点F ，连接DE ，则 $\frac{D E}{A C}$ 的值为．

查看解析
7、如图，以正方形ABCD顶点A为圆心，对角线AC为半径作弧交边AD延长线于点E ，若AB＝4，则图中阴影部分的面积为（结果保留π）．

查看解析
8、如图，在矩形ABCD中，AB＝8cm ， BC＝4cm ．将矩形ABCD沿EF折叠，使点A与点C重合，则EB的长为 cm ．

查看解析
9、若关于x的一元二次方程x²﹣5x+a＝0的一个根是3，则a的值为．

查看解析
10、数学的美无处不在．数学家们研究发现，弹拨琴弦发出声音的音调高低，取决于弦的长度，绷得一样紧的几根弦，如果长度的比能够表示成整数的比，发出的声音就比较和谐．例如，三根弦长度之比是15：12：10，把它们绷得一样紧，用同样的力弹拨，它们将分别发出很调和的乐声do、mi、so ．研究15、12、10这三个数的倒数发现： $\frac{1}{12} - \frac{1}{15} = \frac{1}{10} - \frac{1}{12}$ ．我们称15、12、10这三个数为一组调和数．现有一组调和数：x、8、5（x＞8），则x的值是（）

A、5 B、10 C、15 D、20

查看解析
11、如图，小茗同学在物理实验操作课中观察光的折射现象，发现水平放置的水杯底部有一束光线从水中射向空气时要发生折射．当入射光线和水杯的底面成75°，折射光线与水杯口平面成65°时，∠1的度数是（）

A、155° B、160° C、165° D、170°

查看解析
12、2025年是乙巳年，其中“乙”是天干，“巳”是地支．天干地支纪年法起源于古代中国的历法制定，用于记录年份、月份、日期等时间单位，由十个天干和十二个地支组成．天干包括甲、乙、丙、丁、戊、己、庚、辛、壬、癸．地支包括子、丑、寅、卯、辰、巳、午、未、申、酉、戍、亥．从“天干”中抽一个，抽到“乙”的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{10}$ C、 $\frac{1}{12}$ D、 $\frac{1}{22}$

查看解析
13、下列各式计算正确的是（）

A、2a（a+1）＝2a²+2a B、a³+a²＝a⁵ C、（﹣ab²）³＝a³b⁶ D、（a﹣b）²＝a²﹣b²

查看解析
14、每年3月21日为“国际森林日”，提醒着人们对森林问题的关注，善待森林即善待人类自己．根据官方数据，深圳市森林碳储量为217.03万吨，将“217.03万”用科学记数法表示为（）

A、21.703×10⁴ B、2.1703×10⁵ C、2.1703×10⁶ D、2.1703×10⁷

查看解析
15、某古村落的斜坡 $A D$ 上有一棵古树 $P Q$ ，斜坡的坡度i为 $1 : 2.4$ ，古树底端Q到坡底A点的距离 $A Q$ 为2.6米．为了保护这棵古树，在距离斜坡底A点4.4米的水平地面上立了一块古树信息牌 $M N$ ，古树 $P Q$ 和古树信息牌 $M N$ 均与地面 $B N$ 垂直．某校数学兴趣小组测得当太阳光线与水平线成 $53 °$ 角时，古树 $P Q$ 落在信息牌上的影子 $E N$ 长为3米，请帮助他们计算出古树 $P Q$ 的高度．（结果精确到0.1，参考数据： $\sin 53 ° \approx 0.8$ ， $\cos 53 ° \approx 0.6$ ， $\tan 53 ° \approx 1.3$ ）

查看解析
16、如图，在平面直角坐标系中，直线 $A B$ 分别交 $x$ 轴， $y$ 轴于点 $B, A, C$ 为 $A B$ 的中点，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象过点 $C$ ，且 $O A = 2, O B = 4$ ．

(1)、求 $k$ 的值；

(2)、求直线 $A B$ 的函数表达式．

查看解析
17、数学老师为了帮助班上的后进生进行“日日清”训练，每天为作业中有多处错误的同学设计A，B，C，D四份基础题，并将基础题写在背面完全相同且大小一样的四张卡片上，然后让这部分同学随机抽取卡片进行过关训练．

(1)、小明同学从A，B，C，D四份基础题中任选一份，选中A的概率是_____；

(2)、小明和小红分别从A，B，C，D四份基础题中随机抽取一份，求这两名同学恰好抽到同一份基础题的概率．

查看解析
18、如图，在 $△ A B C$ 中；点 $O$ 为 $A B$ 边上一点， $⊙ O$ 经过 $B 、 D$ 两点，交 $B C$ 于点 $E$ ，交 $A B$ 于点 $F$ ， $∠ C D B = ∠ D F B$ ．

(1)、求证： $A C$ 是 $⊙ O$ 的切线；

(2)、若 $A D = 5$ ， $A B = 10$ ，求 $⊙ O$ 的半径．

查看解析
19、如图， $A C$ 是正方形 $A B C D$ 的对角线，将 $△ A C D$ 绕着点A逆时针旋转 $60 °$ 得到 $△ A E F$ ．

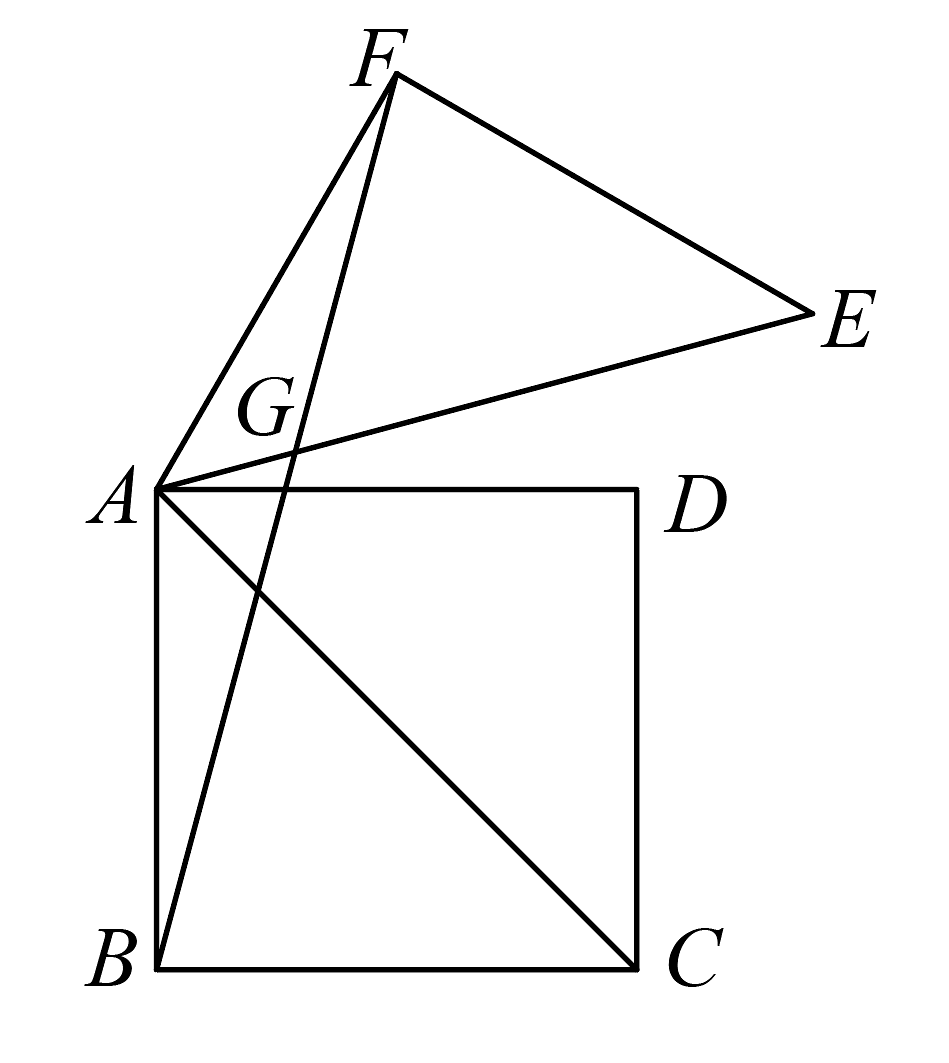(1)、求证：B，D，E三点共线；

(2)、连接 $B F$ ，交 $A E$ 于点G，求 $∠ E G F$ 的度数．

查看解析
20、为了满足人们对于精神文明的需求，某社区决定逐年增加微型图书阅览室的投入．已知2023年投入资金2万元，2025年投入资金 $2.88$ 万元，假定每年投入资金的增长率相同，求该社区2023年至2025年投入资金的增长率．

查看解析

上一页 296 297 298 299 300 下一页跳转

月份	销售量/个		销售额/元
月份	滨滨	妮妮	销售额/元
1月	80	50	6800
2月	100	60	8400

组别	体重（kg）	频数（人）
A	39.5～46.5	2
B	46.5～53.5	a
C	53.5～60.5	8
D	60.5～67.5	5
E	67.5～74.5	4