-
1、 张老师带领x名学生到某动物园参观,已知成人票每张10元,学生票每张5元,设门票的总费用为y元,则y关于x的函数表达式可表示为.
-
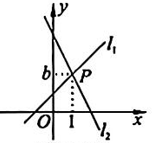
2、 如图,直线 与直线 相交于点P(1,b),则关于x,y的方程组 的解是.
-
3、 已知一次函数y= kx+b的图象经过点(1,0),且y随x的增大而减小,写出一个满足条件的一次函数的表达式为.
-
4、 已知函数y=2x-3,当y<5时,x的取值范围是.
-
5、 若直线y=2x-1经过点(a,3),则a的值为.
-
6、 如图,直线y=x+2与y轴相交于点过点作x轴的平行线交直线y=0.5x+1于点过点 作y轴的平行线交直线y=x+2于点再过点 作x轴的平行线交直线y=0.5x+1于点 , 过点B2作y轴的平行线交直线y=x+2于点 , 依此类推,得到直线y=x+2上的点 , 与直线y=0.5x+1上的点. 则 的长为( )
 A、64 B、128 C、256 D、512
A、64 B、128 C、256 D、512 -
7、 如图,在平面直角坐标系中,点A的坐标为(0,3),△ABO沿x轴向右平移得到△A'B'O',点A的对应点A'在直线 上,则点B与其对应点B'间的距离是( )
 A、 B、3 C、4 D、5
A、 B、3 C、4 D、5 -
8、 阳光中学举行学生运动会,小汪和小勇参加了800米跑.路程s(米)与时间t(分钟)之间的函数图象如图所示,两位同学在跑步中均保持匀速,则下列说法错误的是( )
 A、小勇的平均速度为160米/分 B、到终点前2分钟,小汪的速度比小勇的速度快80米/分 C、小勇和小汪同时达到终点 D、小汪和小勇的平均速度相等
A、小勇的平均速度为160米/分 B、到终点前2分钟,小汪的速度比小勇的速度快80米/分 C、小勇和小汪同时达到终点 D、小汪和小勇的平均速度相等 -
9、 一次函数y=3x-6的图象与y轴的交点坐标是( )A、(2,0) B、(0,2) C、(0,-6) D、(-6,0)
-
10、 若正比例函数y= kx的图象经过点(1,-3),则k的值为( )A、 B、 C、3 D、-3
-
11、 下列选项中的函数,y是x的正比例函数的是( )A、y=2x-1 B、 C、 D、y=-2x
-
12、 如图,一次函数与坐标轴分别交于A,B两点,C是AB的中点,且C的横坐标为 , 过点C,B分别作x轴、y轴的垂线,交于点D,点E,B为垂足.
 (1)、b=;(2)、过点C作交x轴于点F,连结BF,求证:直线AB平分(3)、求EF的长.
(1)、b=;(2)、过点C作交x轴于点F,连结BF,求证:直线AB平分(3)、求EF的长. -
13、 小嘉同学想要挑战“自制弹簧测力计”项目,为此他需要了解弹簧在弹性限度内的弹簧长度与拉力的关系,再根据实验数据制作弹簧测力计.经过测量,他得到5组拉力读数x(N)与弹簧长度之间的数据,如表所示:
x(N)
1
2
3
4
5
y(cm)
3.6
5.2
6.8
8.4
10
 (1)、请在如图的平面直角坐标系中描出各点(x,y),能否用你学过的函数模型来刻画两个变量之间的关系? 若能,试求出y关于x的函数表达式;(2)、当弹簧长度为7.6cm时,物体拉力是多少?
(1)、请在如图的平面直角坐标系中描出各点(x,y),能否用你学过的函数模型来刻画两个变量之间的关系? 若能,试求出y关于x的函数表达式;(2)、当弹簧长度为7.6cm时,物体拉力是多少? -
14、 如图,在△ABC中,AC=AB,AD⊥BC,过点C作CE∥AB,∠BCE=70°,连结ED并延长ED交AB于点F.
 (1)、求∠CAD的度数;(2)、求证:△CDE≌△BDF.
(1)、求∠CAD的度数;(2)、求证:△CDE≌△BDF. -
15、 如图,D是△ABC内部的一点,BD=CD,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,且BE=CF.
 (1)、求证:∠DBE=∠DCF;(2)、求证:△ABC为等腰三角形.
(1)、求证:∠DBE=∠DCF;(2)、求证:△ABC为等腰三角形. -
16、解不等式组 并把解集在数轴上表示出来.

-
17、 如图,在长方形ABCD中,AB=5,BC=8,E,F是边BC上的两点,连结AE,DF,将和△CDF沿AE,DF折叠后,点B和点C重合于点M,则EF的长是.

-
18、 在全民健身环城越野赛中,甲、乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示.有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中说法正确的序号是.

-
19、 定义:若三角形满足其中两边之和等于第三边的三倍,则称该三角形为“三倍三角形”.若等腰△ABC是三倍三角形,且其中一边长为3,则的周长为.
-
20、 如图,直线y=2x和y=ax+4交于点A(m,3),则不等式 的解为.
