-
1、在平面直角坐标系中,已知点 , 点 , 则直线与(填“x”或“y”)轴平行.
-
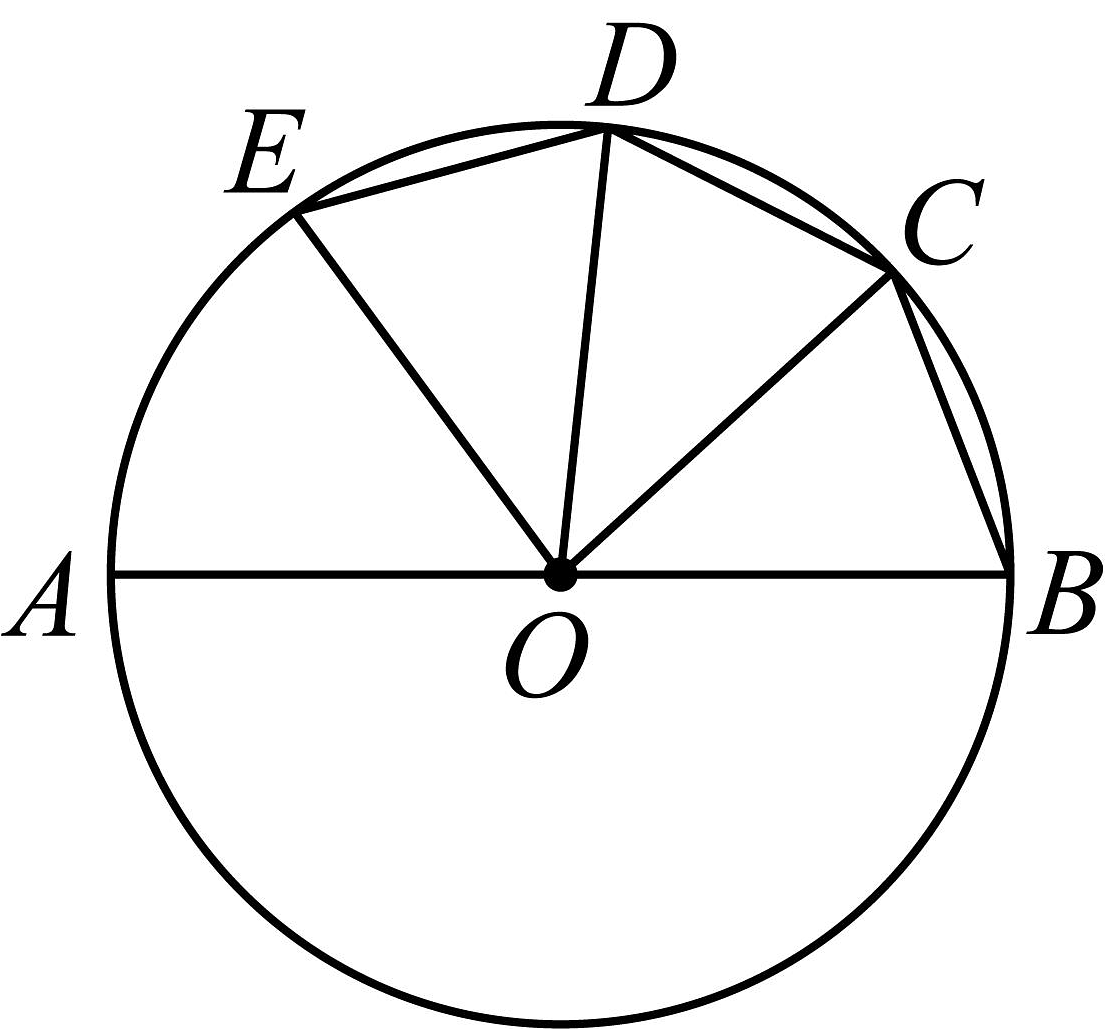
2、如图,已知是的直径, , , 那么弧度数等于 .
-
3、若 , 互为相反数, , 互为倒数,则 .
-
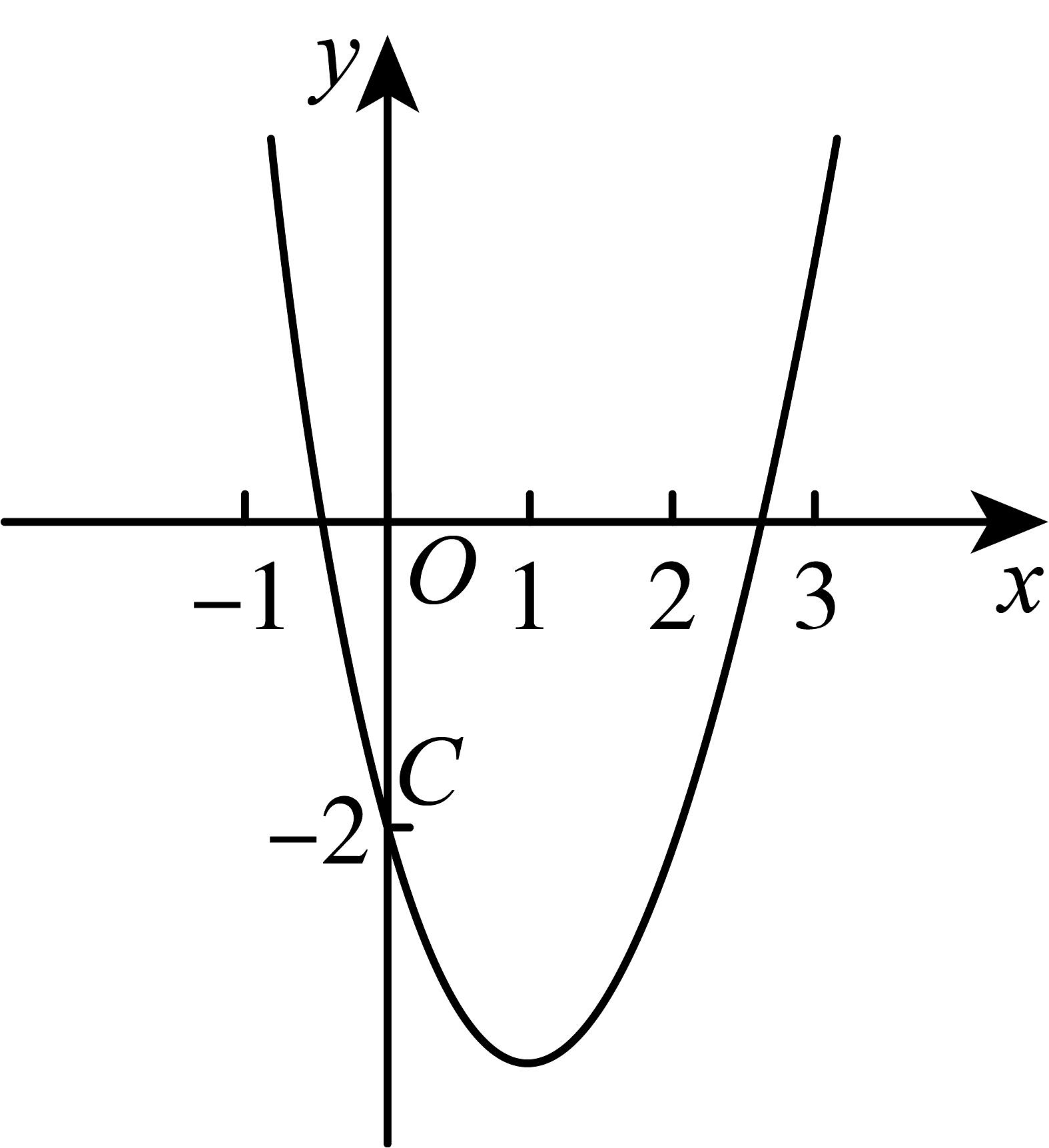
4、如图,已知抛物线过点与x轴交点的横坐标分别为 , , 且 , , 则下列结论:
①;
②方程有两个不相等的实数根;
③;
④;
⑤ . 其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
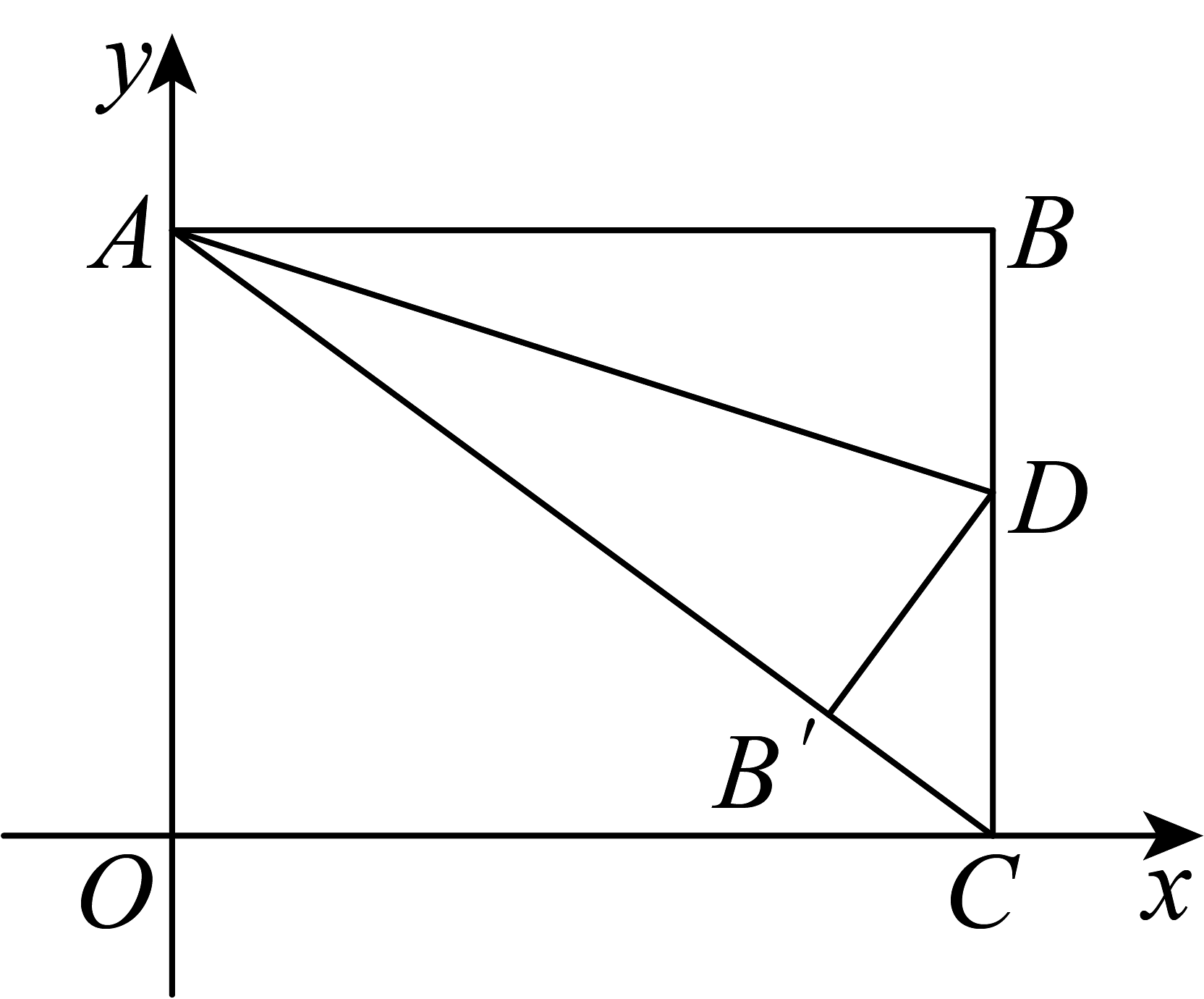
5、如图,在平面直角坐标系中,四边形为矩形,点 , 分别在轴、轴上,且点 , 为边上一点,将沿所在直线翻折,当点的对应点恰好落在对角线上时,点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、按一定规律排列的单项式: . 则第7个单项式是( )A、 B、 C、 D、
-
7、下列调查样本中最适合用普查的是( )A、了解一批电视机的使用寿命 B、了解我市居民的年人均收入 C、了解我市学生的视力情况 D、了解某校学生的课外阅读情况
-
8、已知 , 求代数式的值.
-
9、如图,已知 , , D为上一点,构造菱形 , 点E在线段上,G为上一点, , 连接交于点H.
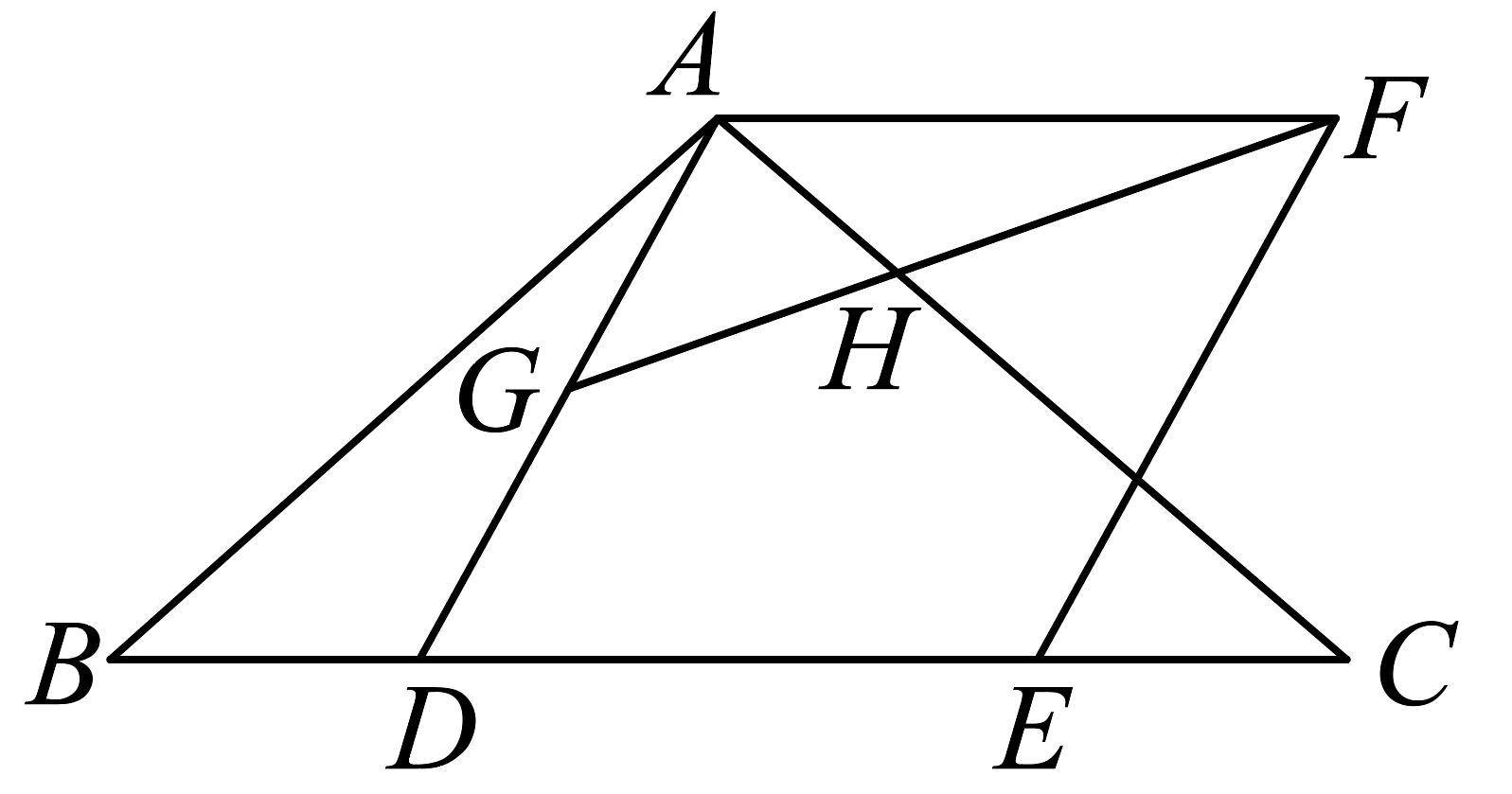 (1)、求证: .(2)、当G为的中点, , 时,求的长.(3)、若 , 求证: .
(1)、求证: .(2)、当G为的中点, , 时,求的长.(3)、若 , 求证: . -
10、如图,在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处保持的速度匀速运动.小聪测量黑球减速后运动距离(单位:cm)随运动时间(单位:s)变化的数据,整理得下表.

运动时间
0
1
2
3
4
…
运动距离
0
14
24
…
探究发现,与之间的数量关系可以用二次函数来描述.
(1)、求关于的函数关系式.(2)、当时,求两球之间的距离.(3)、黑球能否追上白球?若能,求出追上时的值;若不能,求出它们之间的最短距离. -
11、如图,四边形为的内接四边形,连结 , 交于点E.若 , .
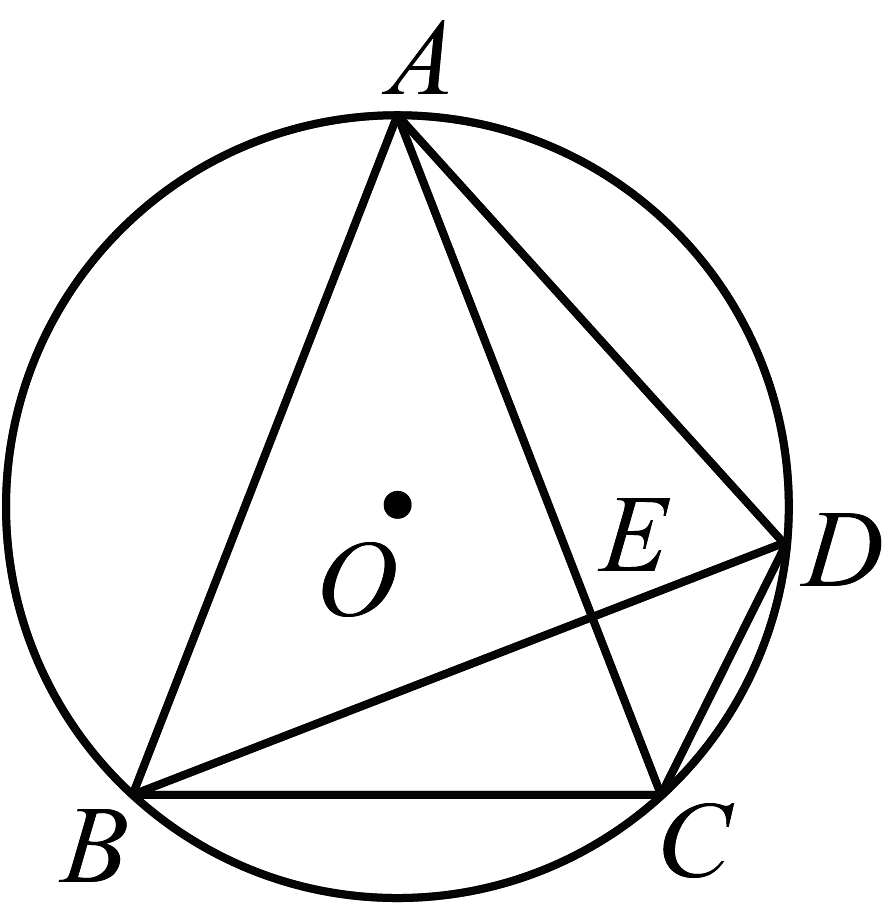 (1)、求的大小(用含的代数式表示).(2)、若 , , 求的长.
(1)、求的大小(用含的代数式表示).(2)、若 , , 求的长. -
12、云南被誉为“彩云之南”,拥有众多令人心动的风景名胜.其中昆明石林风景区、丽江玉龙雪山、大理古城、香格里拉普达措国家公园更是成为了打卡必去的旅游景点.某校兴趣小组准备调查同学们今年暑假最想去的旅游景点(每位同学只能选择一个),设定了“A.昆明石林风景区;B.丽江玉龙雪山;C.大理古城;D.香格里拉普达措国家公园”四个景点进行调查.
【收集数据】
(1)在确定调查方案时,小李同学设计了三种方案:
方案①:调查七年级的部分女生;
方案②:调查每个班级综合素质评价得分前10名学生;
方案③:每个班随机抽取一定数量的学生进行调查.
其中,最具有代表性的一个方案是____________(填序号).
【整理数据】
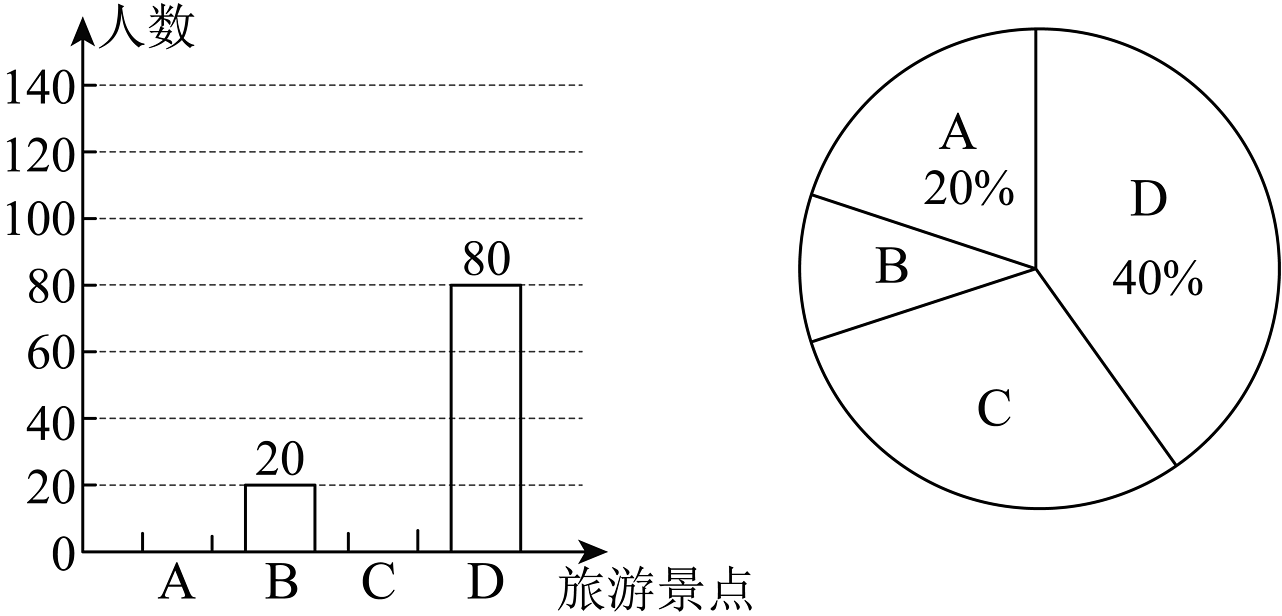
(2)小李采用了最具有代表性的方案,用收集到的数据绘制出两幅不完整的统计图,请你根
据图中信息,完成下列任务:
①该校随机抽取了____________名同学参加问卷调查;
②补全条形统计图;
③在扇形统计图中,C景点对应的扇形圆心角的度数为____________.
【分析数据】
(3)若该校共有学生2500人,请你估计最想去大理古城的学生有多少人?
-
13、计算: .
-
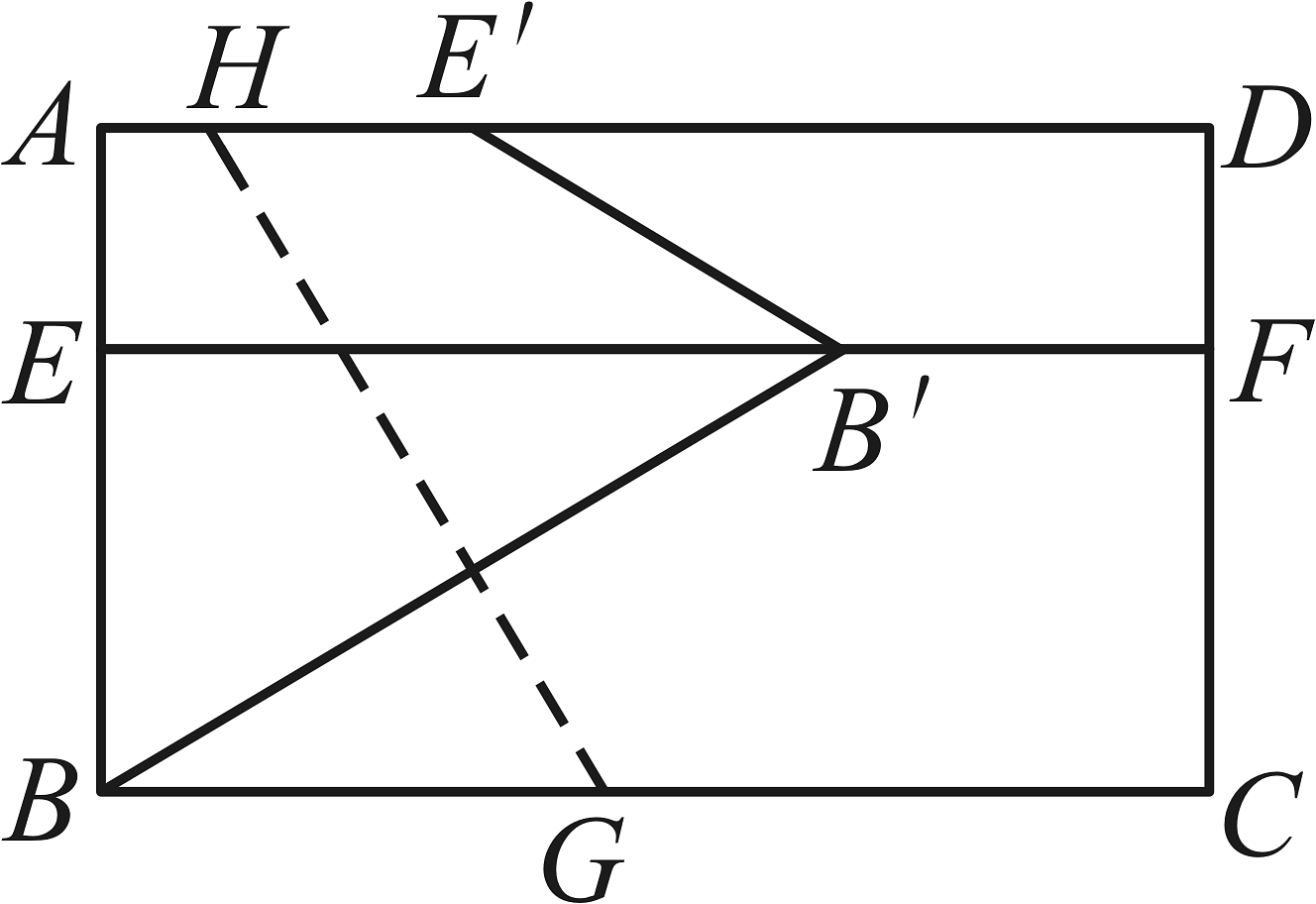
14、如图,矩形中,点E,F,G,H分别在 , , , 上, , 连接 , 作线段关于直线对称的线段 , 点 , 恰好落在线段 , 上,则 .
-
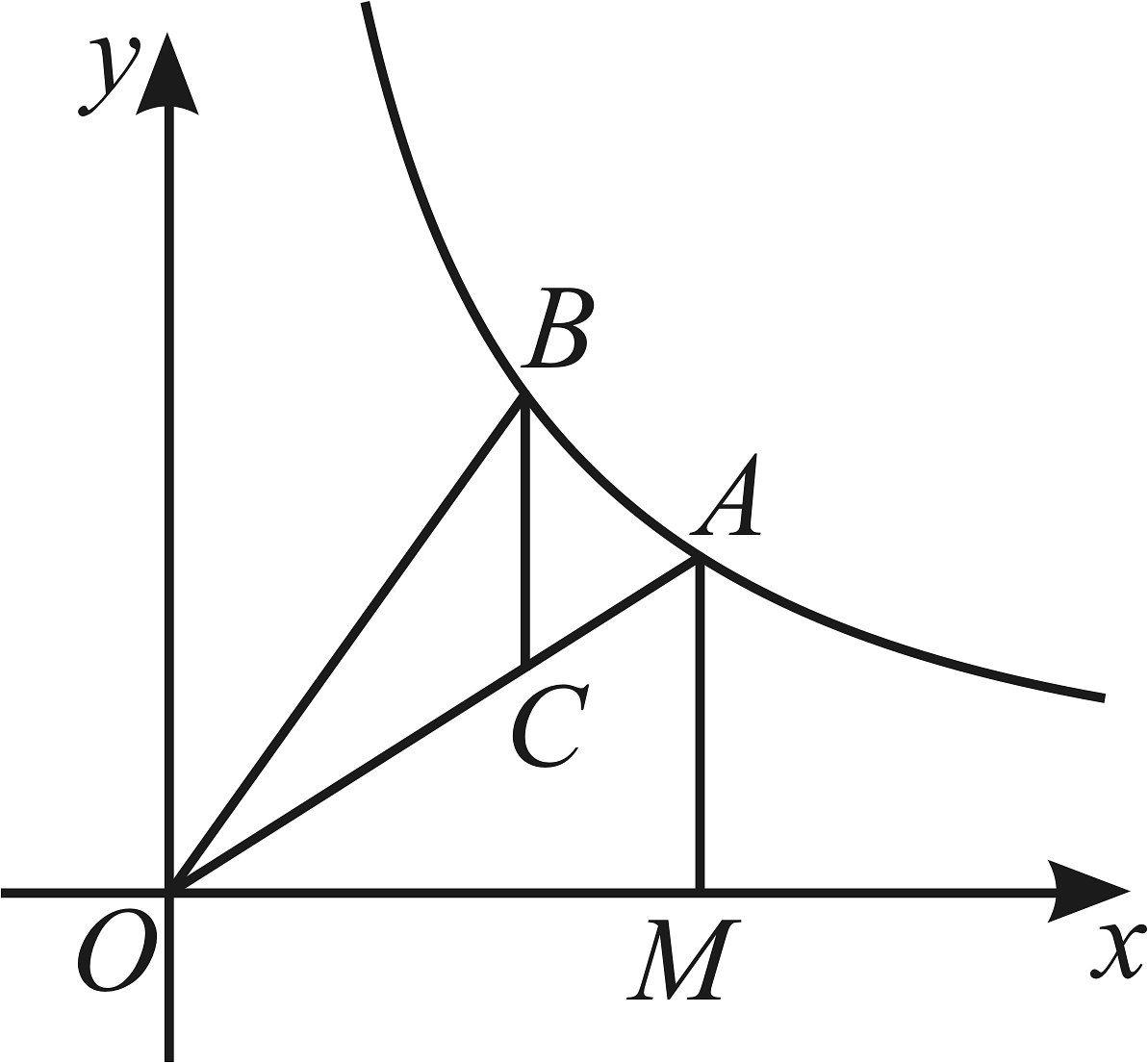
15、如图,点A,B在反比例函数的图象上,轴于点M,交线段于点C,连结 . 已知点A,B的横坐标分别为6,4.则的值为 .
-
16、如图是由正方形所组成的网格,点A,B,C分别在格点上,则的值为 .

-
17、如图,在中, , 分别切 , , 于点D,E,F.若 , 则 .

-
18、因式分解: .
-
19、如图所示,在中, , 以其三边为边向外作正方形.作 , 且 , 达·芬奇通过四边形旋转与四边形重合的思路证明了勾股定理.若 , 四边形的面积 , 则的长是( )
 A、4 B、 C、 D、
A、4 B、 C、 D、 -
20、抛物线经过 , , 三点,且该抛物线与x轴的交点位于y轴两侧,则 , , 的大小关系是( )A、 B、 C、 D、