-
1、如图,圆锥的底面半径 , 高 , 该圆锥的侧面积是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图所示电路中,随机闭合 , , 中的两个,能让其中一个灯泡发光的概率是( )
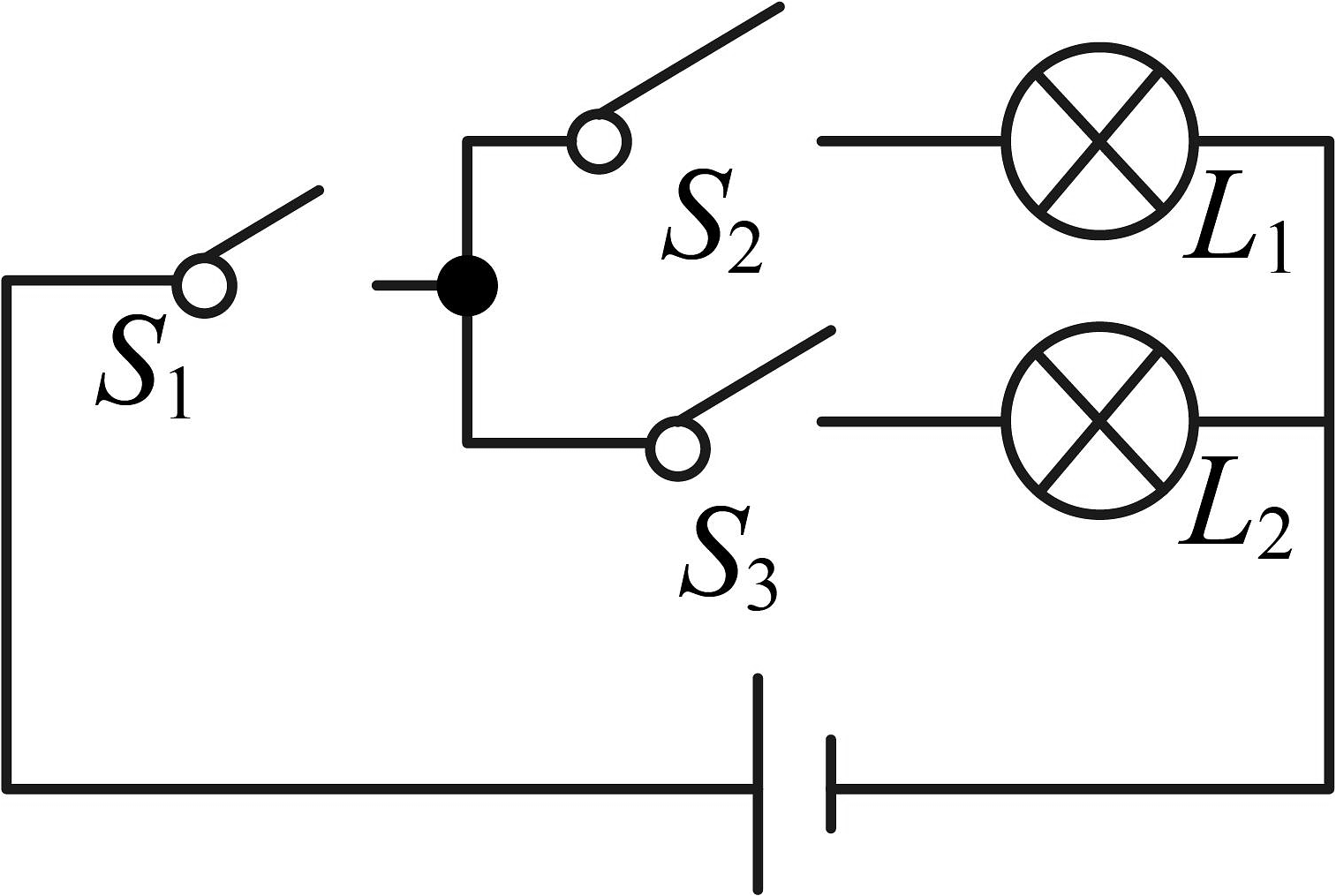 A、 B、 C、 D、1
A、 B、 C、 D、1 -
3、对某班同学课外活动最喜欢的项目进行问卷调查(每人选一项),绘制成如图所示的统计图.已知参与问卷的总人数为60人,则选“踢毽子”的人数为( )
 A、9人 B、12人 C、15人 D、24人
A、9人 B、12人 C、15人 D、24人 -
4、如图是一个正方体的平面展开图,若“家”字为正方体的上面,则该正方体下面的字是( )
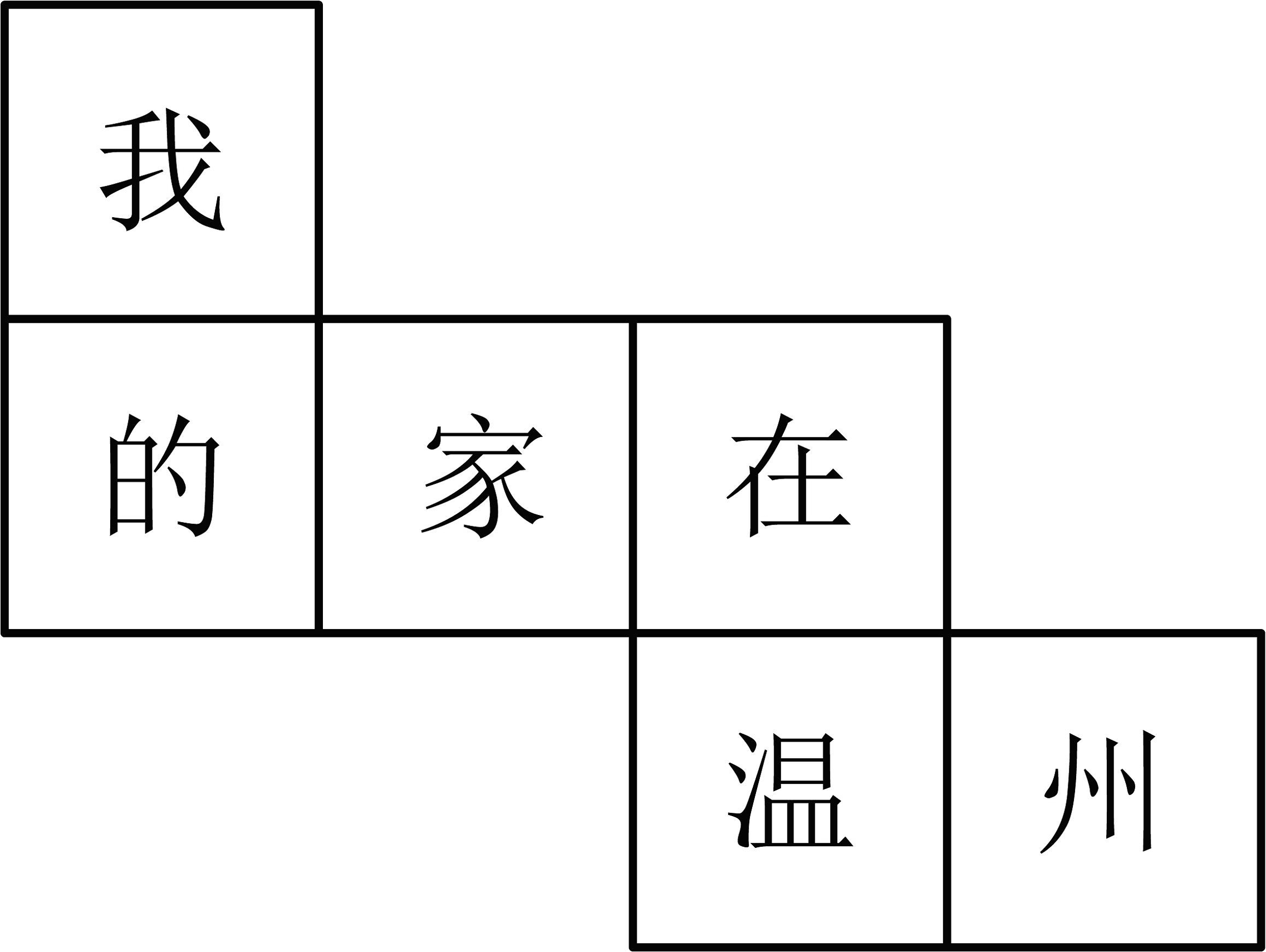 A、我 B、在 C、温 D、州
A、我 B、在 C、温 D、州 -
5、计算的结果为( )A、 B、 C、 D、
-
6、发布后,截至年月,其国内月度下载量约为次.其中数据用科学记数法表示为( )A、 B、 C、 D、
-
7、如图,在中,是钝角,以上一点O为圆心,为弦作 .
 (1)、在图中作出交于点D(不写作法,保留作图痕迹);(2)、若 .
(1)、在图中作出交于点D(不写作法,保留作图痕迹);(2)、若 .①求证:是的切线;
② , , 求弦的长.
-
8、一次函数的图象与反比例函数的图象相交于 , 两点.
 (1)、求反比例函数的解析式;(2)、以直线x=2为对称轴,作直线的轴对称图形,交x轴于点C,连接AC,求AC的长度.
(1)、求反比例函数的解析式;(2)、以直线x=2为对称轴,作直线的轴对称图形,交x轴于点C,连接AC,求AC的长度. -
9、无人机在实际生活中应用广泛.如图所示,小明利用无人机测量大楼的高度,无人机在空中P处,测得楼楼顶D处的俯角为 , 测得楼楼顶A处的俯角为.已知楼和楼之间的距离为100米,楼的高度为10米,从楼的A处测得楼的D处的仰角为(点A、B、C、D、P在同一平面内).
 (1)、填空:______.(2)、求此时无人机距离地面高度.
(1)、填空:______.(2)、求此时无人机距离地面高度. -
10、为庆祝中国共产党成立100周年,某校举行“学党史·感党恩”知识竞答活动.甲、乙两班各选出5名学生参加竞赛,其竞赛成绩(满分为100分)如表所示:
甲班
1号
2号
3号
4号
5号
80分
80分
80分
100分
90分
乙班
6号
7号
8号
9号
10号
80分
100分
85分
70分
95分
(1)、写出甲、乙两个班这10名学生竞赛成绩的中位数和众数:(2)、若从甲、乙两班竞赛成绩“≥90分”的4名学生中随机抽取2名参加全区党史知识竞赛,求这2名学生恰好来自同一个班的概率. -
11、已知 .(1)、化简P;(2)、若 , 求P的值.
-
12、如图,已知点E在平行四边形ABCD边DA延长线上,且AE=AD.求证:四边形AEBC是平行四边形.

-
13、解不等式组:
-
14、如图是一张菱形纸片 , 点E在边上, , 把沿直线折叠得到 , 点落在的延长线上.若恰好平分 , 则°, .

-
15、如图,每个小正方形的边长为1,在中,点D为的中点,则 .

-
16、如图,在纸上剪一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径 , 扇形的半径为R,扇形的圆心角等于 , 则R的值是 .

-
17、已知抛物线与x轴交于点和(点A在点B的左侧),对称轴为 , 直线与抛物线相交于两点 , , 则最小值为( )A、4 B、 C、2 D、
-
18、我国古代数学名著《九章算术》中对正负数的概念注有“今两算得失相反,要令正负以名之”.如收入100元记为元,那么支出60元记为( )A、元 B、60元 C、元 D、40元
-
19、 综合与探究
【探索发现】如图1,小军用两个大小不同的等腰直角三角板拼接成一个四边形.
【抽象定义】以等腰三角形为边向外作等腰三角形,使该边所对的的角等于原等腰三角形的顶角,此时该四边形称为“双等四边形”,原等腰三角形称为四边形的“伴随三角形”.如图2,在中, , .此时,四边形ABCD是“双等四边形”, 是“伴随三角形”.

 (1)、【问题解决】如图3,在四边形ABCD中,AB=AC,AD=CD,
(1)、【问题解决】如图3,在四边形ABCD中,AB=AC,AD=CD,求:
①AD与BC的位置关系为:;
②.(填“>”,“<”或“=”)(2)、【方法应用】①如图 4,△ABC中,AB=BC,将 绕点 A 逆时针旋转至 , 点 D 恰好落在 BC 边上,求证:四边形 ABDE 是双等四边形.②如图 5,在等腰三角形 ABC 中, , , AB=5,在平面内找一点 D,使四边形 ABCD 是以 为伴随三角形的双等四边形. 若存在,请求出 CD 的长. 若不存在,请说明理由.
-
20、【问题背景】排队是生活中常见的场景,如图,某数学小组针对某次演出,研究了排队人数与安检时间,安排通道数之间的关系

【研究条件】条件1:观众进场立即排队安检,在任意时刻都满足:排队人数=现场总人数-已入场人数;
条件2:若该演出场地最多可开放9条安检通道,平均每条通道每分钟可安检6人.
【模型构建】若该演出前30分钟开始进行安检,经研究发现,现场总人数y与安检时间x之间满足关系式:结合上述信息,请完成下述问题:
(1)、 若开设 3 条安检通道, 安检时间为 x 分钟, 则已入场人数为 (用 x 表示), 若排队人数为 w, 则 w 与 x 的函数表达式.(2)、【模型应用】 在(1)的条件下, 当安检时间在几分钟时, 排队人数达到最大值? 最大值为多少?(3)、已知该演出主办方要求:
①排队人数在 10 分钟内 (包含 10 分钟) 减少;
②尽量少安排安检通道,以节省开支.
若同时满足以上两个要求,可开设几条安检通道,请说明理由?
【总结反思】
函数可刻画生活实际场景,但要注意验证模型的正确性,未来可结合更多变量(如突发情况、安检流程优化等)进行更深入的分析,以提高模型的准确性和实用性.