相关试卷

1、若（x-2025）²+（x-2026）²=5，则（x-2025）（x-2026）的值是（）

A、-2 B、-1 C、1 D、2

查看解析
2、已知（2x-8）（3x-4）-（3x-4）（x-13）可分解因式为（3x+a）（x+b），则a+2b的值是（）

A、1 B、6 C、7 D、8

查看解析
3、如图，将三角形ABC沿BC方向平移得到三角形DEF，若BF=7，EC=1，则平移的距离是（）

A、3 B、4 C、6 D、8

查看解析
4、如图，直线AB与CD相交于点O，OB平分∠DOE.若∠DOE=60°，则∠AOE的度数是（）

A、140° B、150° C、160° D、170°

查看解析
5、下列多项式中，能运用平方差公式分解因式的是（）

A、 $- 4 x^{2} + 9 y^{2}$ B、 $- 4 x^{2} - 9 y^{2}$ C、 $4 x^{2} + 9 y^{2}$ D、 $4 x^{2} + 4 x y + y^{2}$

查看解析
6、计算 $(- a^{2})^{3}$ 的结果是（）

A、 $- a^{5}$ B、 $- a^{6}$ C、 $a^{5}$ D、 $a^{4}$

查看解析
7、质检部门为了检测某品牌电器的质量，从同一批次共10000件产品中随机抽取100件进行检测，检测出次品5件，由此估计这一批次产品中的次品件数是（）

A、5 B、100 C、500 D、1000

查看解析
8、空气由多种气体混合而成，为了直观介绍空气中各成分的百分比，最适合使用的统计图是（）

A、条形统计图 B、折线统计图 C、扇形统计图 D、频数直方图

查看解析
9、要使分式 $\frac{x - 2}{3 + x}$ 的值为0，则x的取值应满足（）

A、x≠-3 B、x≠2 C、x=-3 D、x=2

查看解析
10、如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法。配方法是一种重要的解决问题的数学方法，能解决一些与非负数有关的问题。如：求代数式的最大值或最小值等。求代数式x²+2x+2的最小值，同学们经过探究、合作、交流，最后得到如下解法：
解：x²+2x+2=（x²+2x+1²-1²）+2=（x+1）²+1. 因为（x+1）²是非负数，所以当（x+1）²=0时，（x+1）²+1的值最小，最小值为1，所以x²+2x+2的最小值是1.

(1)、求代数式y²-5y-4的最小值.

(2)、求代数式 $k^{2} + \frac{1}{k^{2}} + 5$ 的最小值.

(3)、求代数式 $k^{2} + 2 k + \frac{4}{k^{2}} - \frac{4}{k} + 3$ 的最小值.

查看解析
11、某校组织七年级师生参加春游活动，有中客车和大客车两种交通工具可供租用，已知1辆中客车可乘坐30人，1辆大客车可乘坐42人，且租用1辆大客车和1辆中客车的费用共900元，2500元能租用的大客车数量与2000元能租用的中客车数量相同。

(1)、分别求出租用1辆大客车的费用和租用一辆中客车的费用.

(2)、若全校师生共504人参加春游活动，那么有哪些不同租车方案可供选择（要求租用的客车都必须坐满）？

(3)、在(2)的条件下，请通过计算说明哪种租车方案最优惠？

查看解析
12、如图，已知 $∠ A E D = ∠ A D E = \frac{1}{2} ∠ B$ ， DE平分 $∠ A D C$ .

(1)、求证： $A D / / B C$ ．

(2)、若CE⊥DE，且 $∠ D A E = ∠ C E A$ ，求 $∠ E C B$ 的度数．

查看解析
13、 $2024$ 年 $4$ 月 $25$ 日 $20$ 时 $59$ 分，神舟十八号载人飞船成功发射，中国载人航天与空间站建设迎来全新的发展 $.$ 为了弘扬航天精神，某中学开展了航天知识竞答活动，学校随机抽取了八年级的部分同学的成绩进行整理 $.$ 数据分成五组， $A$ 组： $50 \leq x < 60$ ； $B$ 组： $60 \leq x < 70$ ； $C$ 组： $70 \leq x < 80$ ； $D$ 组： $80 \leq x < 90$ ； $E$ 组： $90 \leq x \leq 100 .$ 根据以上数据，我们绘制了频数分布直方图和扇形统计图．

根据以上信息，解答下列问题：

(1)、本次随机抽查_▲_名同学，并补全频数分布直方图；

(2)、扇形统计图中， $C$ 组所在扇形的圆心角为度；

(3)、规定本次航天知识竞赛活动成绩在 $80$ 分及以上的成绩为优秀，全校共有 $2000$ 名学生，请估计全校取得优秀成绩的同学共有多少？

查看解析
14、先化简： $(\frac{2 a - 3}{a - 2} - 1) \div \frac{a^{2} - 1}{a - 2} - \frac{2}{a - 1}$ ，并在 $- 2$ ， $- 1$ ， $1$ ， $2$ 中选一个合适的值代入求值．

查看解析
15、分解因式：

(1)、 $a^{3} - 2 a^{2} + a$ ．

(2)、 $x^{3} y - x y^{3}$ ．

查看解析
16、解方程 $($ 组 $)$ ：

(1)、 $\{\begin{array}{l} 2 x + 3 y = 8 \\ 3 x - y = 1 \end{array}$

(2)、 $\frac{2 x - 7}{x - 2} - \frac{3}{2 - x} = 1$ ．

查看解析
17、计算：

(1)、 $(- 1)^{2025} + (π - 3.14)^{0} + {(- \frac{1}{3})}^{- 2}$ ．

(2)、 $(2 x - y)^{2} - (x + y) (- x + y)$ ．

查看解析
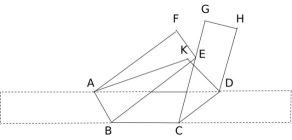
18、如图，将一张长方形纸带进行了两次折叠，折痕分别为AB，CD，线段BE交CG于点E， $∠ F A D$ 的平分线与 $∠$ HDA的平分线相交于点K. 若 $∠$ FEG=60°，则 $∠$ AKD的度数为．

查看解析
19、若实数x满足 $(x - 2025) (2020 - x) = \frac{9}{4}$ ，则x= ．

查看解析
20、关于 $x$ 的方程 $\frac{3 x + 1}{x + 1} - \frac{n}{x + 1} = 1$ 有增根，则 $n$ 的值是．

查看解析

上一页 602 603 604 605 606 下一页跳转