相关试卷

1、测量跳远项目的成绩时，老师会测量学生后脚跟落地点到起跳线的垂线段长度。现一学生跳远训练情况如图所示，点A表示后脚跟落点，点B表示前脚跟落点，AC，BD垂直于起跳线l，垂足分别为C，D，则测量成绩的线段是（）

A、AE B、AC C、AD D、BD

查看解析
2、下列运算的结果正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $(a^{2})^{3} = a^{6}$ C、 $(a b)^{3} = a b^{3}$ D、 $a^{6} \div a^{3} = a^{2}$

查看解析
3、要使分式 $\frac{x - 1}{x + 3}$ 的值为0，则 $x$ 的值是（）

A、-3 B、-1 C、1 D、3

查看解析
4、如图，统计七年级部分女生的跳远成绩，得到频数直方图（每组含前一个边界值，不含后一个边界值）。跳远成绩在1.46m（含1.46m）以上的人数为（）

A、13 B、20 C、33 D、46

查看解析
5、我国科研团队于今年研发的全球首例128比特光量子芯片登上《自然》封面。芯片每个组件定位精度达到0.000000002米。数据0.000000002用科学记数法表示为（）

A、 $2 \times 1 0^{- 9}$ B、 $20 \times 1 0^{- 8}$ C、 $0.2 \times 1 0^{- 10}$ D、 $2 \times 1 0^{- 8}$

查看解析
6、如图，AB，DE被AC所截，则∠A的内错角是（）

A、∠1 B、∠2 C、Z3 D、∠4

查看解析
7、如图1，某一动直线AB分别截两平行直线a，b于点A，B，点 C为直线b上（位于点B右侧）一点，满足∠BAC=30°，∠BCA角平分线CD交直线a于点D.在直线a上，点D左侧任取一点E，点A右侧任取一点F；在直线b上，点B左侧任取一点G，点C右侧任取一点H.CD右边取点I满足CILCD，满足∠CDI=45°，DI交直线AB于点J，∠JAD的角平分线交DI于点K. 设∠ABC=α(0°<α<180°且α≠60°).

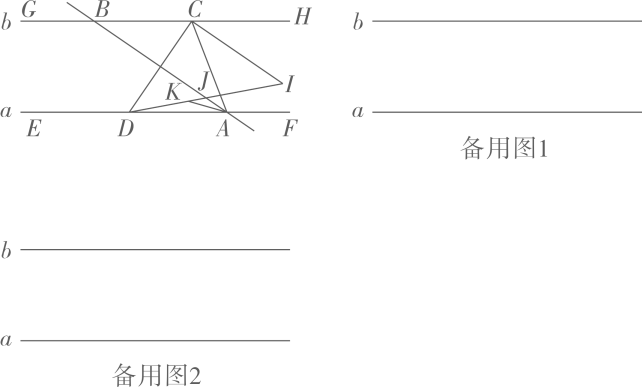(1)、若α=30°，求∠CAF-∠KAD的度数，写出过程；若α=90°，直接写出∠CAF-∠KAD的度数；

(2)、若∠CAF-∠KAD=0°，求α的度数；

(3)、若|∠CAK-110|=60°，求α的度数.

查看解析
8、规定一种新的运算“ $Δ (a^{x})$ ”，其中 $a \neq 0$ ， x为正整数.其运算规则如下：① $Δ (a^{x}) = x a^{x - 1}$ ；② $b Δ (a^{x}) = b x a^{x - 1}$ （其中b为常数）.

(1)、计算： $Δ (a^{3}) =$ ， $\frac{1}{2} Δ (a) =$ ；

(2)、已知 $p Δ (a^{3}) + q Δ (a^{2}) = 2 a - 6 a^{2}$ ，求p，q的值.

(3)、已知 $p Δ (a^{3}) + q Δ (a^{2}) + \frac{1}{m} Δ (a) = (q - 1) a^{2} + (2 p + 6) a - \frac{1}{n} + 1$ （其中m，n均不为0），化简并计算： $\frac{4 p m - 2 m n + q n}{(m - 1) (n - 1) m n}$ .

查看解析
9、2025年蛇年春晚吉祥物“已升升”，其形象既憨态可掬，又富有古意，深受大家喜爱，某商店，第一次用3000元购进一批吉祥物“已升升”，很快售完；该商店第二次购进吉祥物“已升升”时，进价提高了20%，同样用3000元购进的数量比第一次少了10件。

(1)、求第一次购进的吉祥物“已升升”每件的进价；

(2)、若两次购进的吉祥物“已升升”每件售价均为80元，且全部售完，求两次的利润总和.

查看解析
10、如图，已知∠1=47°，∠2=133°，∠A=∠F.

(1)、求证：AE//BF；

(2)、若∠C=56°，求∠D的度数.

查看解析
11、某校为七年级学生提供了“科学实验”“趣味棋艺”，“喵历史”，“时光合唱”四种课后服务项目，为了解学生最喜欢哪个项目，随机抽取了该校七年级部分学生进行调查，根据调查结果，绘制了如下两幅尚不完整的统计表和扇形统计图，请你根据统计图提供的信息，解答下列问题：

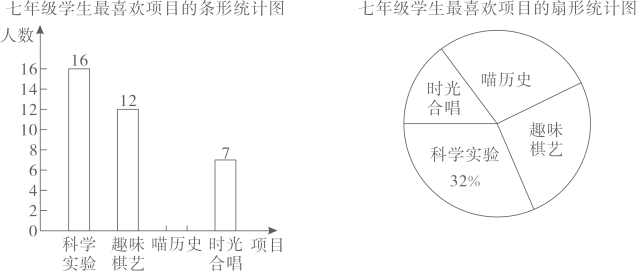(1)、本次被抽查的学生有多少名？

(2)、请补全条形统计图；“喵历史”项目所对应的扇形圆心角度数为多少度？

(3)、若该校七年级学生有600人，根据抽查结果，试估计全校七年级喜欢“趣味棋艺”项目的学生有多少人？

查看解析
12、先化简，再求值： $(\frac{2 x - 3}{x - 2} - 1) \div \frac{x^{2} - 2 x + 1}{x - 2}$ ，然后再从1，2，3中选一个合适的数作为x的值，求式子的值.

查看解析
13、解下列方程（组）：

(1)、 ${\begin{array}{l} 2 x - y = 3 \\ x + y = 6 \end{array}$

(2)、 $\frac{2}{1 - x} + 1 = \frac{x}{1 + x}$

查看解析
14、计算：

(1)、 $(- 3)^{2} + (π + \sqrt{5})^{0} + 2^{- 2}$

(2)、 $(x + 1)^{2} + (x + 1) (x - 1)$

查看解析
15、现有甲、乙、丙三张不同的正方形纸片（如图1）.将三张纸片按图2，图3两种不同方式放置于同一矩形中，记图2中阴影部分周长为 $C_{1}$ ，面积 $S_{1}$ ；图3中阴影部分周长为 $C_{2}$ ，面积为 $S_{2}$ .已知 ${\begin{array}{l} 3 C_{1} = 2 C_{2} \\ S_{2} - S_{1} = \frac{1}{6} C_{1} C_{2} \end{array}$ ，则 $\frac{b}{a} - \frac{c}{b} =$ .

查看解析
16、甲、乙两个小马虎，在解方程组 ${\begin{array}{l} a x + y = 10 \\ x + b y = 7 \end{array}$ 时，由于粗心，甲看错了方程组中的a，得到方程组的解为 ${\begin{array}{l} x = 1 \\ y = 6 \end{array}$ ，乙看错了方程组中的b，得到方程组的解为 ${\begin{array}{l} x = - 1 \\ y = 12 \end{array}$ ，则原方程组正确的解是.

查看解析
17、若关于x的分式方程 $\frac{m}{x^{2} - 9} + \frac{2}{x + 3} = \frac{1}{x - 3}$ 有增根 $x = 3$ ，则m的值是.

查看解析
18、如图，已知AB//DE，∠B=75°，∠D=140°，则∠C=.

查看解析
19、某中学随机抽取了10名学生，统计他们上一年参与志愿者活动的次数，数据如下（单位：次）：3，5，2，4，3，6，4，5，3，1，则志愿者活动次数是3的频率是.

查看解析
20、已知方程3x+2y=6，用关于x的代数式表示y，则y=.

查看解析

上一页 601 602 603 604 605 下一页跳转