-
1、如图,在平行四边形ABCD中,点E , F分别在边BC , AD上,BE=DF , 连接AE , CF , AC .
 (1)、求证:四边形AECF为平行四边形.(2)、若CF=AF=5,AC=8,求四边形AECF的面积.
(1)、求证:四边形AECF为平行四边形.(2)、若CF=AF=5,AC=8,求四边形AECF的面积. -
2、李老师要从小聪、小亮两人中选拔一人参加知识竞赛,现对两人的5次测试成绩进行整理分析,两人的成绩如下:
小聪:76,80,79,85,80;
小亮:77,79,81,82,81.
李老师将两人的成绩分析如下:(单位:分).
平均成绩
中位数
众数
小聪
a
80
c
小亮
80
b
81
(1)、填空:a= ;b= ;c= .(2)、李老师已经求得小聪5次测试成绩的方差S2=8.4,请你帮助李老师计算小亮5次测试成绩的方差.(3)、根据以上信息,请你运用所学的统计知识帮助李老师作出选择,并说明理由. -
3、已知关于x的一元二次方程x2+bx﹣12=0.(1)、当b=4时,求方程的解.(2)、若x=3是方程的一个解,求b的值和方程的另一个解.
-
4、计算:(1)、;(2)、 .
-
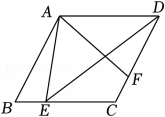
5、如图,在菱形ABCD中,点E , F分别在BC , CD上,BE=CF , 连接AE , AF , DE . 若菱形面积为 , AB=14,四边形AECF的面积是△ABE面积的3.5倍,则线段ED的长为 .
-
6、在直角坐标系中,函数y=k1x与函数的函数图象交于点A(﹣3,m),B(n , 5),则k2的值为 .
-
7、某位射击运动员的10次射击训练成绩统计如下:
成绩/环
6
7
8
9
10
次数
1
1
3
4
1
则10次成绩的中位数为环.
-
8、如图,在平行四边形ABCD中,对角线AC , BD交于点O , AC⊥BC , 若AC=4,AB=5,则对角线BD的长为 . .

-
9、若一个八边形的每个外角都相等,则它的一个内角等于度.
-
10、已知点M(x1 , n),N(x2 , n+2)都在反比例函数(a为实数)的图象上,( )A、若x1x2<0,则﹣2<n<0 B、若x1x2>0,则n<﹣2 C、若n<0,则x1﹣x2<0 D、若n>﹣2,则x1﹣x2>0
-
11、如图,在Rt△ABC中,∠BAC=90°,将它向右平移得到Rt△A'B'C',AC和A'B'交于点D , 延长BA , C'A'交于点E , 若BC'=7,B'C=3,则线段DE的长为( )
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5 -
12、随着生产技术的进步,某款药品的生产成本逐年下降.两年前生产1吨药品的成本是5000元,现在生产1吨该款药品的成本是3000元,设药品成本的年平均下降率为x , 则可列方程( )A、2×3000(1﹣x)=5000 B、3000(1﹣x)2=5000 C、2×5000(1﹣x)=3000 D、5000(1﹣x)2=3000
-
13、如图,在四边形ABCD中,对角线AC , BD交于点O , AO=CO , BO=DO . ( )
 A、若AC⊥BD , 则AO=BO B、若AC⊥BD , 则∠BAC=∠DAC C、若AC=BD , 则∠ABD=∠CBD D、若AC=BD , 则AB=BC
A、若AC⊥BD , 则AO=BO B、若AC⊥BD , 则∠BAC=∠DAC C、若AC=BD , 则∠ABD=∠CBD D、若AC=BD , 则AB=BC -
14、如图,点A在反比例函数的图象上,AM⊥y轴于点M , 若△AOM 的面积为4,则k的值为( )
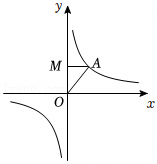 A、﹣8 B、﹣4 C、4 D、8
A、﹣8 B、﹣4 C、4 D、8 -
15、给出一组数据:a , b , c , c , d(a<b<c<d),将这组数据改变为a﹣2,b , c , c , d+2后,比较这两组数据,统计量一定发生变化的是( )A、平均数 B、中位数 C、方差 D、众数
-
16、若关于x的一元二次方程x2﹣mx+2=0有两个不相等的实数根,则m的值可以是( )A、2 B、1 C、﹣2 D、﹣3
-
17、下列各式运算正确的是( )A、 B、 C、 D、
-
18、已知反比例函数的图象经过点A(2,﹣3),则函数图象一定还经过( )A、(1,6) B、(3,2) C、(﹣6,1) D、(﹣3,﹣2)
-
19、以下图标中,既是轴对称图形又是中心对称图形的是( )A、
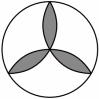 B、
B、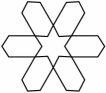 C、
C、 D、
D、
-
20、如图是象棋棋盘一部分示意图,建立平面直角坐标系,使“将”位于点 , “相”位于点 , 若“相”走一步(“相”只能沿着棋盘走“田”字格),那么“相”的新位置位于点( )
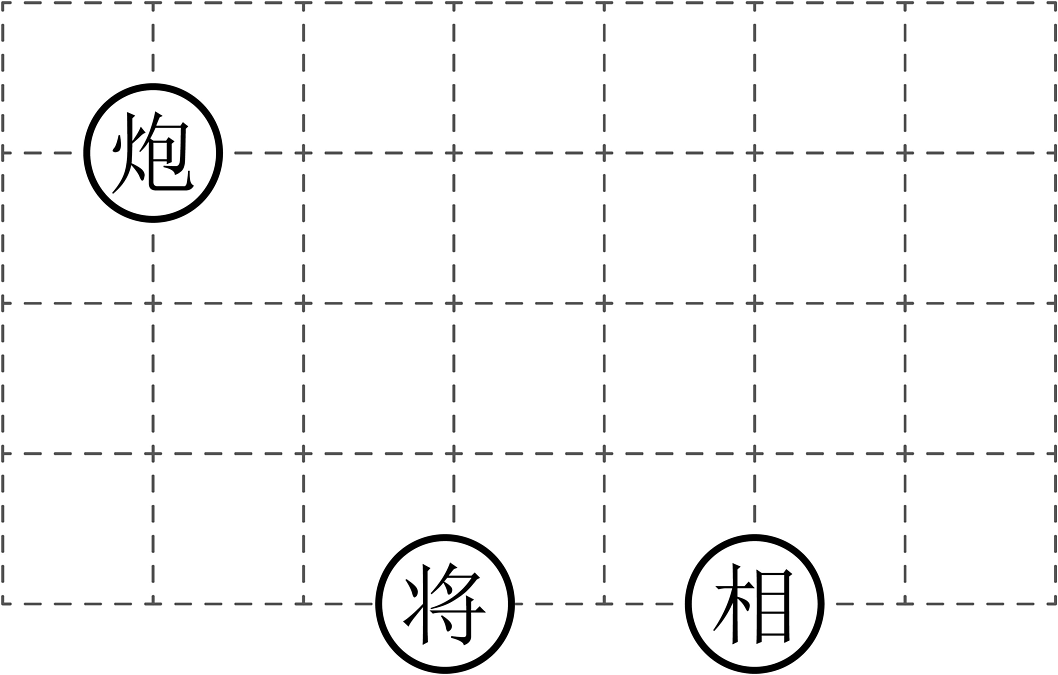 A、 B、或 C、 D、或
A、 B、或 C、 D、或