相关试卷

1、如图， $D$ 是 $B C$ 上一点， $D E / / A B$ ，交 $A C$ 于点 $E$ ，点 $F$ 在 $A B$ 边上，且 $∠ A = ∠ 1$ ．

(1)、判断 $D F$ ， $A C$ 的位置关系，并说明理由；

(2)、若 $∠ B + ∠ C = 115^{\circ}$ ，求 $∠ 1$ 的度数．

查看解析
2、某校组织开展了丰富多彩的主题活动，设置了“ $A$ ：诗歌朗诵表演， $B$ ：歌舞表演， $C$ ：书画作品展览， $D$ ：手工作品展览”四个专项，每个学生只能报名参加其中一个专项．为了解活动开展情况，学校随机抽取了部分学生进行调查，绘制了如图所示的不完整的条形统计图和扇形统计图．

(1)、本次随机调查的学生人数是人．

(2)、请你补全条形统计图．

(3)、在扇形统计图中，“ $B$ ”所在扇形的圆心角为度．

(4)、若该校有学生 $1800$ 人，则全校选择 $D$ ：手工作品展览的学生约有多少人？

查看解析
3、如图，按要求作答．

(1)、将 $▵ A B C$ 向右平移 $5$ 格，得 $▵ A' B' C'$ ，画出 $▵ A' B' C'$ ．

(2)、已知 $∠ C = 45^{\circ}$ ，则 $∠ C'$ 的度数是多少？

查看解析
4、解方程 $($ 组 $)$ ：

(1)、 $\{\begin{array}{l} 2 x - y = 9 ① \\ 3 x + y = 6 ② \end{array}$

(2)、 $\frac{3}{x - 4} - 1 = \frac{2}{4 - x}$

查看解析
5、计算或化简

(1)、 ${(- 1)}^{2022} + {(2023 - π)}^{0} + {(- \frac{1}{2})}^{- 2}$ ；

(2)、 $(3 - x) (3 + x) + x (x - 2)$ ．

查看解析
6、图 $1$ 是一款落地的平板支撑架， $A B$ ， $B C$ 是可转动的支撑杆．调整支撑杆使得其侧面示意图如图 $2$ 所示，此时平板 $D E / / A F$ ， $∠ B A F = ∠ B C E$ ， $∠ B = 84^{\circ}$ ，则 $∠ B C D =$ $^{\circ}$ ；现将支撑杆 $A B$ 调整至图 $3$ 所示位置，调整过程中 $∠ B$ ， $∠ B C E$ 大小不变， $∠ B A F = 146^{\circ}$ ，再顺时针调整平板 $D E$ 至 $D' E'$ ，使得 $D' E' / / A F$ ，则 $∠ D C D' =$ ．

查看解析
7、已知 $\{\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于 $x, y$ 的二元一次方程 $a x + y = 5$ 的一个解，那么 $a$ 的值是．

查看解析
8、下列各式从左到右的变形，属于因式分解的是( )

A、 $(x + 2) (x - 2) = x^{2} - 4$ B、 $x^{2} - y^{2} = (x + y) (x - y)$ C、 $x + 2 y = (x + y) + y$ D、 $x^{2} - 2 x - 1 = (x - 1)^{2}$

查看解析
9、下列各式计算正确的是( )

A、 $a^{3} + a^{3} = a^{6}$ B、 ${(a b)}^{2} = a b^{2}$ C、 $3 a \cdot 3 a = 9 a$ D、 $a^{7} \div a^{3} = a^{4}$

查看解析
10、如图，已知直线 $a 、 b$ 被直线 $c$ 所截，那么 $∠ 1$ 的内错角是( )

A、 $∠ 2$ B、 $∠ 3$ C、 $∠ 4$ D、 $∠ 5$

查看解析
11、空气的密度为 $0.00129 g / c m^{3}$ ， $0.00129$ 这个数用科学记数法可表示为( )

A、 $0.129 \times 10^{- 2}$ B、 $1.29 \times 10^{- 2}$ C、 $1.29 \times 10^{- 3}$ D、 $12.9 \times 10^{- 1}$

查看解析
12、下列调查中，适合全面调查的是( )

A、七年级数学课本中的错别字 B、某品牌护眼灯的使用寿命 C、五一长假期间某景点的游客流量 D、浙江省中小学生的睡眠情况

查看解析

13、活动与探究

解码蜜蜂的“家”——为什么蜂房是正六边形的?

蜜蜂的“集体宿舍”是由多个正六边形密铺在一起的，这些密铺的正六边形使得蜂房之间没有空隙，一点儿也不浪费空间.这是数学中的密铺(或镶嵌)问题.平面图形的密铺(或镶嵌)是指用形状、大小完全相同的一种或多种平面图形进行拼接，使彼此之间不留空隙、不重叠地铺成一片.

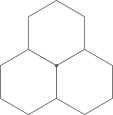(1)、探究一：若只用一种正多边形，哪些正多边形可以密铺?

平面图形	每个内角度数	能否整除	能否密铺
正三角形	60°	360°÷60°=6	能
正方形	①	②	能
正五边形	108°	$360 ° \div 108 ° = \frac{10}{3}$	不能
正六边形	120°	$360 ° \div 120 ° = 3$	能
正七边形	900° 7	$360 ° \div \frac{900 °}{7} = \frac{14}{5}$	不能
正八边形	135°	③	④
…	…	…

请补全上述表格①； ②； ③； ④.

(2)、探究二：在能密铺的正多边形中，哪种形状最省材料?

数学视角：蜜蜂的身体可近似看成圆柱，若圆柱底面半径为1，当蜂房恰好容纳一只蜜蜂即正多边形的内切圆半径均为1时，比较正三角形，正方形和正六边形周长的大小.

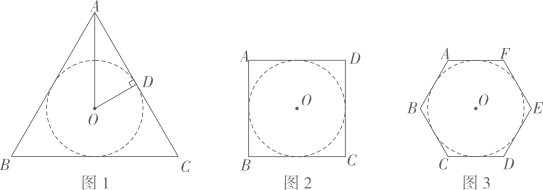
观察图1，发现⊙O是正三角形ABC的内切圆，与AC切于点D ， ( $O D ⟂ A D,$ $∠ O A D = 3 0^{\circ}, O D = 1,$ ，在Rt△ADO中， . $A D = \sqrt{3},$ 则 $△ A B C$ 的周长为( $6 \sqrt{3} .$

①如图2，正方形ABCD的周长为；

②如图3，求出正六边形的周长(写出求解过程).

(3)、探究三：在能密铺的正多边形中，哪种形状可以使蜜蜂的活动空间最大?

数学视角：假设蜜蜂建造蜂房的材料总量即周长一定，比较正三角形、正方形和正六边形面积的大小.

若正多边形的周长都为12，则正三角形的面积为；正方形的面积为；正六边形的面积为.

【得出结论】综上所述：在相同条件下，正六边形结构最省材料，能使蜜蜂的活动空间最大，是建造蜂房的最优方案.

查看解析

14、在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 3 (a \neq 0)$ 与x轴交于A ， B两点，点B的坐标为(1，0)，点 C(2，5)在抛物线上.

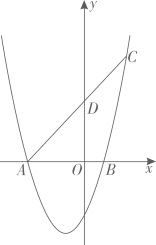(1)、求抛物线的解析式；

(2)、 ①求点A的坐标；
②当y＜0时，根据图象直接写出x的取值范围；

(3)、连接AC交y轴于点D ，在y轴上是否存在点 P ，使 $△ A C P$ 是以AC为直角边的直角三角形，若存在，请直接写出所有符合条件的点P坐标，若不存在，请说明理由.

查看解析
15、为了让学生体验青海民俗文化，某学校开设了特色艺术实践课程，课程分别是：A.五谷画，B.彩陶，C.剪纸，D.排灯.现学校要了解学生最感兴趣的课程情况，从全校学生中随机抽取部分学生进行调查(每位学生必选且只能选一个课程)，根据调查结果，绘制了如下两幅不完整的统计图：
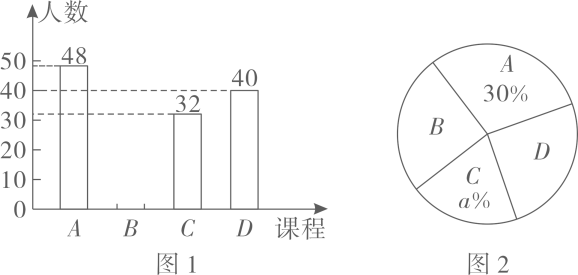
根据以上提供的信息，解答下列问题：

(1)、此次被调查的学生总人数为；扇形统计图中 $a =$ ；

(2)、补全条形统计图；

(3)、该校有1600人，请你估计该校对课程D感兴趣的学生有多少名?

(4)、甲、乙两名同学从A、B、C、D四个课程中任选一个，用树状图或列表法求两人恰好选到同一个课程的概率.

查看解析
16、如图，线段AB经过圆心O ，交⊙O于点A ， C ， AD为⊙O的弦，连接BD ， ∠A=∠B=30°.

(1)、求证：直线 BD是⊙O的切线；

(2)、已知BC=2，求 $\hat{D C}$ 的长(结果保留π).

查看解析
17、数学实践
【问题背景】中国传统农业智慧遇上现代数学模型.“豇豆不上架，产量少一半”的农谚流传至今，现代科学揭示了其秘密：当支架与地面形成( $6 5^{\circ}$ °夹角时，既能在早春聚热防冻害，又能在盛夏分散强光，就像给豇豆装了智能遮阳篷.
【问题呈现】用两根竹竿交叉，斜插入地面，交叉点在何处会使支架与地面形成65°夹角?
【模型建立】环节一：数据收集
两根竹竿长度均为 1.8米，插入地下的部分为 0.3米，竹竿与地面接触点间距为 0.6米且与地面所形成的夹角均为 $6 5^{\circ} .$
环节二：数学抽象
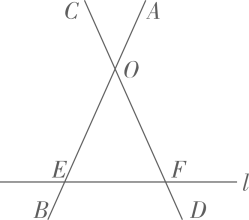
如图：已知线段AB与CD交于点O ， AB ， CD与直线l分别交于点E ， F ， $A B = C D = 1.8 m,$ $B E = D F = 0.3 m, ∠ A E F = ∠ C F E = 6 5^{\circ}, E F = 0.6 m,$ 求 OE的长度.(结果精确到0.1，参考数据： $s i n 6 5^{\circ} \approx 0.91, c o s 6 5^{\circ} \approx 0.42, t a n 6 5^{\circ} \approx 2.14)$
【模型求解】

【问题总结】交叉点O 距顶端A的长度即 OA为 m时，支架与地面形成( $6 5^{\circ}$ 夹角，这样更贴合作物的生长规律.

查看解析
18、如图，在 $△ A B C$ 中，点O ， D分别是边AB ， BC的中点，过点A作 $A E ‖ B C$ 交DO的延长线于点 E ，连接AD ， BE.

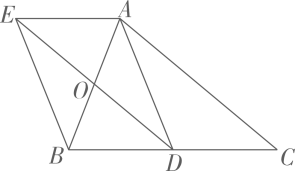(1)、求证：四边形AEBD是平行四边形；

(2)、若AB=AC ，试判断四边形AEBD的形状；并证明.

查看解析
19、如图，直线. $y = - x + b$ 与x轴交于点A(1，0)，与y轴交于点B ，与反比例函数 $y = \frac{m}{x}$ (m为常数， $m \neq 0)$ 的图象在第二象限交于点 $C (- 1, a) .$

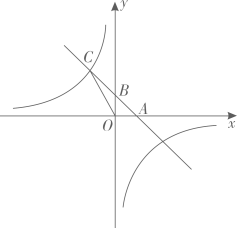(1)、求反比例函数的解析式；

(2)、求 $△ B O C$ 的面积.

查看解析
20、先化简 $(1 - \frac{a}{a + 2}) \div \frac{2}{a^{2} - 4},$ 再从-2，0，1中选一个合适的数代入求值.

查看解析

上一页 448 449 450 451 452 下一页跳转