-
1、计算:
-
2、下图是谢尔宾斯基地毯图案的形成过程.按此规律下去,第⑥个图形中黑色三角形的个数是.

-
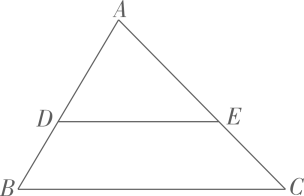
3、 如图, 在 中, 且 3, DB=2, 则 的值是.
-
4、 如图, 在菱形ABCD中, , E , F分别为AB , BC的中点, 且. 则菱形 ABCD的面积为.

-
5、在平面直角坐标系中,点 )在第三象限,则a的取值范围是.
-
6、 若 是一元二次方程 的一个根,则c的值为.
-
7、 七名同学一分钟排球垫球个数分别为 42, 47, 43, 43, 45, 43, 46. 这组数据的众数是.
-
8、实数a , b在数轴上对应点的位置如图所示,则a+b0. (填 “>” “=”或“<”)

-
9、如图,甲、乙两车从A地出发前往B地,在整个行程中,汽车离开A地的路程y(km)与时刻t之间的对应关系如图所示,下列结论错误的是( )
 A、乙车先到达B地 B、A、B两地相距300km C、甲车的平均速度为 100km/h D、在8:30时,乙车追上甲车
A、乙车先到达B地 B、A、B两地相距300km C、甲车的平均速度为 100km/h D、在8:30时,乙车追上甲车 -
10、 如图, AB是⊙O的直径, ∠CAB=40°, 则∠ADC的度数是( )
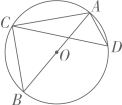 A、80° B、50° C、40° D、25°
A、80° B、50° C、40° D、25° -
11、我国明代数学著作《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.试问各位善算者,多少人分多少银?”译文:“隔着墙壁听见客人在分银两,不知道有多少人,多少银两.若每人分7两,则还多4两;若每人分9两,则还差8两.请问:有多少客人?分多少银两?”设客人为x人,银两为y两.根据题意可列方程组为( )A、 B、 C、 D、
-
12、下列计算正确的是( )A、 B、 C、 D、
-
13、工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA , OB上分别取 OM=ON , 移动角尺,使角尺两边相同的刻度分别与点M , N重合,即CM=CN , 过角尺顶点 C的射线 OC便是∠AOB的平分线,这种做法的依据是( )
 A、AAS B、SAS C、SSS D、ASA
A、AAS B、SAS C、SSS D、ASA -
14、2025年4 月 19 日,全球首次“人机共跑”半程马拉松在北京开跑.本次比赛全程约21公里,这意味着采用双足步态的人形机器人要完成约 25 万次精密关节运动.将数据“250000”用科学记数法表示为( )A、 B、 C、 D、
-
15、下列图形是轴对称图形的是 ( )A、
 B、
B、 C、
C、 D、
D、
-
16、 - (-2)的值为( )A、 B、2 C、- 2 D、
-
17、如图,在正方形ABCD中,点E是对角线AC上的一个动点(不与点A , C重合),连接BE , 点C关于直线BE的对称点为点F , 连接BF , EF .
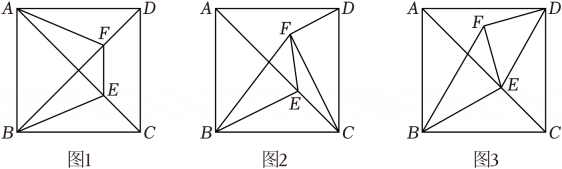 (1)、如图1,若点F恰好落在对角线BD上,连接AF , 求∠CAF的度数.(2)、如图2,连接DF , CF , 若DF∥BE , 试判断线段DF与CF的数量关系和位置关系,并说明理由.(3)、如图3,连接DF , DE , 记△DEF的面积为S1 , △BEF的面积为S2 , 若DF⊥FE , 求的值.
(1)、如图1,若点F恰好落在对角线BD上,连接AF , 求∠CAF的度数.(2)、如图2,连接DF , CF , 若DF∥BE , 试判断线段DF与CF的数量关系和位置关系,并说明理由.(3)、如图3,连接DF , DE , 记△DEF的面积为S1 , △BEF的面积为S2 , 若DF⊥FE , 求的值. -
18、某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元
…
12
14
16
18
20
…
销售量y/盒
…
56
52
48
44
40
…
(1)、求y关于x的函数表达式;(2)、糖果销售单价定为多少元时,所获日销售利润为448元?(3)、超市决定从售出的每盒糖果所获的利润中拿出2元捐赠给儿童福利院,那么该种糖果的日销售利润去掉捐款后可以为400元吗?若可以,请求出该糖果的销售单价;若不可以,请说明理由. -
19、综合与实践
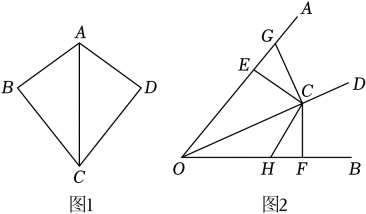
定义学习:若一个四边形有一组对角互补(即对角之和为180°),则称这个四边形为“圆满四边形”.
(1)、概念理解:在①矩形,②菱形中,是“圆满四边形”的是 ;(请填写序号)(2)、性质探究:如图1,已知四边形ABCD是“圆满四边形”,若AB=AD=3,CB=CD , 对角线AC=5,求四边形ABCD的周长.(3)、判定探究:如图2,已知OD平分∠AOB , 点C在射线OD上,CE⊥OA于点E , CF⊥OB于点F , 点G在射线EA上,点H在线段OF上,EG=FH , 连接CG , CH . 求证:四边形GOHC为“圆满四边形”. -
20、在直角坐标系中,函数和函数y2=﹣x+b(k≠0,k , b为常数)的图象交于点A(﹣1,4)和点B .(1)、求函数y1 , y2的表达式.(2)、求点B的坐标,并直接写出当y1<y2时,自变量x的取值范围.(3)、设坐标原点为O , 求△ABO的面积.