-
1、抛物线与x轴的一个交点是(-1,0),则抛物线与x轴的另一个交点坐标是( )A、(0,0) B、(3,0) C、(-3,0) D、(0,-3)
-
2、如图,在△ABC中,∠ACB=9O°,点D在边AC上,AE⊥BD交BD的延长线于E.
 (1)、若AD是△BAE角平分线,说明∠ABD与∠CBD的数量关系:(2)、若点D同时在AB的垂直平分线上,求证CD=DE;(3)、若AC=BC,BD是∠ABC的角平分线,直接写出AE与BD的数量关系.
(1)、若AD是△BAE角平分线,说明∠ABD与∠CBD的数量关系:(2)、若点D同时在AB的垂直平分线上,求证CD=DE;(3)、若AC=BC,BD是∠ABC的角平分线,直接写出AE与BD的数量关系. -
3、如图,∠ABC和∠ACD的平分线交于点E,过E作EG⊥BA交BA的延长线于点G,EF⊥AC交AC于点F.
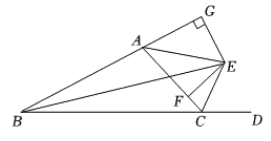 (1)、求证:EG=EF;(2)、连结AE,求证:∠AEG=∠AEF.
(1)、求证:EG=EF;(2)、连结AE,求证:∠AEG=∠AEF. -
4、如图,在三角形ABC中,过点B,A作BD⊥AC,AE⊥BC,BD,AE交千点F,若∠BAC=45°,AD=5,CD=2,求线段BF的长度.

-
5、如图,AB交DE于点F, , 点C在线段AB上, , .
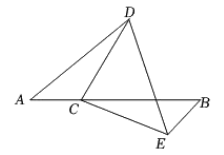 (1)、求证:.(2)、若 , , 求的度数.
(1)、求证:.(2)、若 , , 求的度数. -
6、先化简 , 再从-3,0,3这三个数中取一个合适的数作为x的值代入求值.
-
7、解方程(组):(1)、(2)、
-
8、计算:(1)、3x(2-x)(2)、.
-
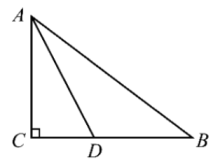
9、如图,在直角△ABC中,∠C=90°,AD是△ABC的角平分线,若AB=6,△ABD的面积为6,则CD的长为.
-
10、如图,作△ABC中,DE垂直平分AC,交AC边于点E,交BC边于点D,若AE=3,△ABD的周长为14,则△ABC的周长为.

-
11、如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与另一束经过光心O的光线相交于点P,点F为焦点,若∠1=α,∠2=β,则∠3的度数表示为( )
 A、а-β B、2a-β C、180°+α-β D、180°-α+β
A、а-β B、2a-β C、180°+α-β D、180°-α+β -
12、古代数学著作《孙子算经》中有“多人共车”问题:今有五人共车,二车空;三人共车,十人步,问人与车各几何?其大意是:每车坐5人,2车空出来;每车坐3人,多出10人无车坐,问人数和车数各多少?设共有x人,y辆车,则可列出的方程组为( )A、 B、 C、 D、
-
13、如图,在△ABC中,AE是△ABC的角平分线,AD是△ABC的高线,∠B=40°,∠C=70°,则∠EAD的度数为( ).
 A、10° B、15° C、20° D、25°
A、10° B、15° C、20° D、25° -
14、如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是1,那么△ABC的面积为( ).
 A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10 -
15、下列等式中,从左到右的变形是因式分解的是( ).A、 B、 C、 D、
-
16、下列运算正确的是( )A、 B、 C、 D、
-
17、如图,当AB//CD,EF与GH不平行时,则下列角中与∠1相等的角是( )
 A、∠2 B、∠3 C、∠4 D、∠5
A、∠2 B、∠3 C、∠4 D、∠5 -
18、已知三角形的两边长分别为5和8,则第三边的长可以是( )A、2 B、3 C、6 D、13
-
19、小明为了方便探究关于x,y的二元一次方程(ax+ by=9(a≠0,b≠0)的解的规律,把x 和y的部分值填入下表.
x
-7
-4
0
2
8
y
10
7
p
1
-5
(1)、p的值为.(2)、下列方程中,与 ax+ by=9组成方程组,在-7<x<8范围内有解的是.(填正确的序号)①2x+y=-5;②x+2y=-4;③3x-y=1.
(3)、已知关于x,y 的二元一次方程 cx+ dy=1(c≠0,d≠0)的部分解如下表所示.x
-7
0
… 8
y
-2
q
·· -
13
求关于x,y的方程组 的解.
-
20、已知实数a,b满足2 021a+2 020b=3,2a+b=1,则的值为.