-
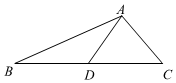
1、如图,在△ABC中,AD是BC边上的中线,AC=3,AD=5,则AB的取值范围是 .
-
2、直角三角形两条边长分别是6和8,则这个直角三角形的第三边长 .
-
3、已知实数 , , , 0.16, , 其中无理数有个.
-
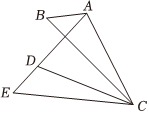
4、如图,在△ABC中,∠BAC=110°,将△ABC绕点C逆时针旋转得到△DEC , 点A , B的对应点分别为D , E , 连接AD , 当点A , D , E在同一条直线上时,则∠BAD的大小是( )
 A、60° B、70° C、40° D、50°
A、60° B、70° C、40° D、50° -
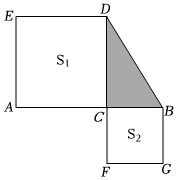
5、如图,点C是线段AB上一点,以AC , BC为边向两边作正方形ACDE和BCFG , 已知AB=10,两正方形的面积和S1+S2=60,则图中阴影部分的面积为( )
 A、10 B、20 C、40 D、25
A、10 B、20 C、40 D、25 -
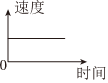
6、一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶,过了一段时间,汽车到达下一车站,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下面能近似刻画汽车速度变化情况的是( )A、
 B、
B、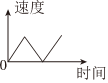 C、
C、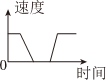 D、
D、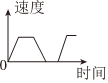
-
7、下列运算正确的是( )A、(-2a)3=-6a3 B、a3-a2=a C、a3•a2=a6 D、a3÷a2=a
-
8、 9的算术平方根是( )A、±3 B、-3 C、3 D、9
-
9、阅读与理解:
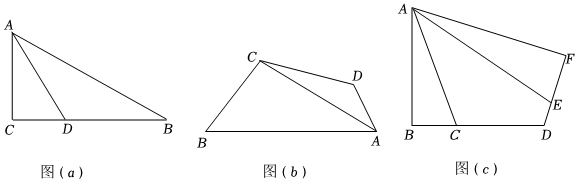
我们曾做过“折纸与证明”的数学活动.折纸,即构造轴对称,常能为我们提供解决问题的思路和方法,例如,在△ABC中,AB>AC(如图),怎样证明∠C>∠B呢?分析:把AC沿∠A的角平分线翻折,因为AB>AC , 所以点C落在AB上的点C'处;即AC=AC' , 据以上操作,易证明△ACD≌△AC'D , 所以∠AC'D=∠C , 一又因为∠AC'D>∠B , 所以∠C>∠B.

【感悟与应用】
(1)、如图(a),在△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB , 试判断CD和BD之间的数量关系,并说明理由;(2)、如图(b),在四边形ABCD中,AC平分∠BAD , AC=25,AD=12,DC=BC=17,求AB的长.(3)、【拓展提高】如图(c),在四边形ABDF中,∠B=∠F=90°,∠BCA=∠AEF , ∠D-∠BAC=90°,若CD=4,AC=5,AE=6,求四边形ABDF的边DE的长.
-
10、 “数形结合”是数学中的一种基本思想方法.我国著名数学家华罗庚对此曾有生动的描述:“数以形而直观,形以数而入微”.下面我们分别以我国三国时期的数学家赵爽(公元3~4世纪)和公元9世纪的阿拉伯数学家阿尔•花拉子在解一元二次方程x2+2x-35=0即x(x+2)=35时的做法为例加以说明.
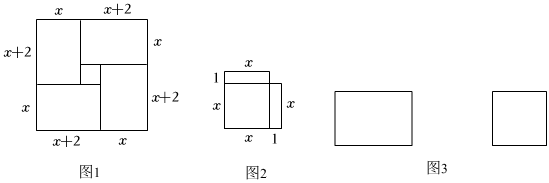
【学习研究】数学家赵爽的做法是,用四个边长分别为x , x+2且面积为x(x+2)=35的矩形构造成图1形状的大正方形,然后用两种方式表示出大正方形的面积,得到(x+2+x)2=4×35+22 , 从而得到一个正数解x=5.阿拉伯数学家阿尔•花拉子米采用的方法是用一个边长为x的正方形和2个边长分别为x , 1的矩形构造出图2的形状(面积为x2+2x=35)并把它补成一个大正方形,然后也是用两种方式表示出大正方形的面积,得到(x+1)2=(x2+2x)+12=35+1,从而得到一个正数解x=5.
(1)、图1中,小正方形的边长为 ▲ , 将图2中补充完整(补充的部分用阴影表示);(2)、【类比迁移】小明想通过以上述构造图形的方法来解一元二次方程方程x2+6x-55=0.①请分别构造以上两种图形,并在图中标注出相关线段的长;(注:第一种方法中已经画好了一个矩形,第二种方法中已经画好了一个正方形,请在已经画好的图形上进行补充)
②请分别根据所画图形,求出方程x2+6x-55=0的一个正数解.
(注:需要写出必要的推算过程)
(3)、【拓展应用】一般地,形如x2+ax=b的一元二次方程可以构造类似以上图形来求解,请选择其中的一种方法,进行图形构造,且在图中标注出相关线段的长,并直接写出该方程的正数解与负数解. -
11、扎染古称“绞缬”,是我国一种古老的纺织品染色技艺.扎染工艺的发展带动了当地旅游相关产业的发展.某扎染坊第一次用3700元购进甲、乙两种布料共80件,其中两种布料的成本价和销售价如表:
单价
类别
成本价/(元/件)
销售价/(元/件)
甲种布料
60
100
乙种布料
40
70
(1)、该扎染坊第一次购进甲、乙两种布料各多少件?(2)、因热销,第一次购进的布料全部售完,该扎染坊第二次以相同的成本价再次购进甲、乙两种布料共100件.若此次购进甲种布料的数量不超过乙种布料数量的1.5倍,且以相同的销售价全部售完这批布料.设第二次购进甲种布料m件,第二次全部售完后获得的利润为W元.第二次应怎样进货,才能使第二次购进的布料全部售完后获得的利润最大?最大利润是多少元? -
12、某校学生会向全校2100名学生发起了“爱心捐助”捐款活动,为了解捐款情况,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如图1、图2所示的统计图.
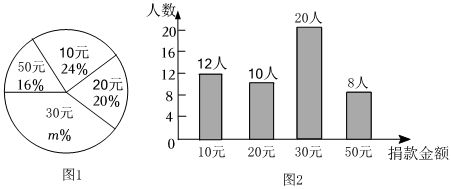
请根据相关信息,解答下列问题:
(1)、本次接受随机调查的学生人数为;(2)、本次调查获取的样本数据的平均数为元、众数为元、中位数为元;(3)、根据样本数据,估计该校本次活动捐款金额不少于30元的学生人数. -
13、用合适的方法解下列方程:(1)、x2-6x+4=0;(2)、2x2-4x=1.
-
14、计算.
-
15、如图,将直角三角形ABC沿着点B到C的方向平移到三角形DEF的位置,此时AB=14cm , DO=6cm , 阴影部分的面积为44cm2 , 则平移的距离为.
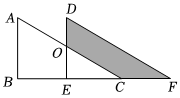
-
16、如图,在平面直角坐标系中,若菱形ABCD的顶点A , B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是.
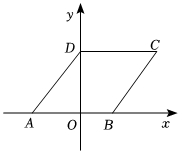
-
17、任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是.
-
18、如图,△ABC中,∠C=90°,AC=BC= , 将△ABC绕点A顺时针方向旋转60°到△AB'C'的位置,连接C'B , 则C'B的长为( )
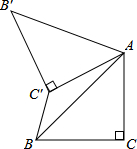 A、2- B、 C、-1 D、1
A、2- B、 C、-1 D、1 -
19、函数的自变量x的取值范围是( )A、x≥0 B、x≠1 C、x≥0且x≠1 D、x>1
-
20、已知关于x的一元二次方程(a+1)x2-2x+a2+a=0有一个根为x=0,则a的值为( )A、0 B、0或-1 C、1 D、-1