相关试卷

1、如图，是某几何体的表面展开图．

(1)、该几何体的名称是________；

(2)、求这个几何体的体积．（结果保留 $π$ ）

查看解析
2、已知单项式 $\frac{5}{6} x^{2} y$ 与 $- 3 x^{n + 1} y$ 是同类项，那么 $n$ 的值是（）

A、 $- 1$ B、 $0$ C、 $1$ D、 $2$

查看解析
3、甲、乙两店卖豆浆，每杯售价均相同．已知甲店的促销方式是：每买2杯，第1杯原价，第2杯半价；乙店的促销方式是；每买3杯，第1、2杯原价，第3杯免费．若东东想买12杯豆浆，则下列所花的钱最少的方式是（）

A、在甲店买12杯 B、在甲店买8杯，在乙店买4杯 C、在甲店买6杯，在乙店买6杯 D、在乙店买12杯

查看解析
4、综合与实践
折纸是一项有趣的活动，折纸活动也伴随着我们初中数学的学习．在折纸过程中，我们可以研究图形的运动和性质，也可以在思考问题的过程中，初步建立几何直观，现在就让我们带着数学的眼光来折纸吧．定义：将纸片折叠，若折叠后的图形恰能拼合成一个无缝隙、无重叠的长方形，这样的长方形称为完美长方形．

(1)、操作发现：
如图1，将 $△ A B C$ 纸片按所示折叠成完美长方形 $E F G H$ ，若 $△ A B C$ 的面积为18， $B C = 6$ ，则此完美长方形的边长 $F G =$ _____，面积为_____．

(2)、类比探究：
如图2，将 $▱ A B C D$ 纸片按所示折叠成完美长方形 $A E F G$ ，若 $▱ A B C D$ 的面积为40， $B C = 8$ ，求完美长方形 $A E F G$ 的周长．

(3)、拓展延伸：
如图3，将 $▱ A B C D$ 纸片按所示折叠成完美长方形 $E F G H$ ，若 $E F : E H = 3 : 4$ ， $A D = 25$ ，求此完美长方形 $E F G H$ 的周长与面积．

查看解析
5、如图， $A B C D$ （ $A D > A B$ ）是一张周长为36厘米的长方形纸片，设长方形纸片的长 $A D$ 为x厘米，将纸片的四个角各剪下一个边长为2厘米的正方形．

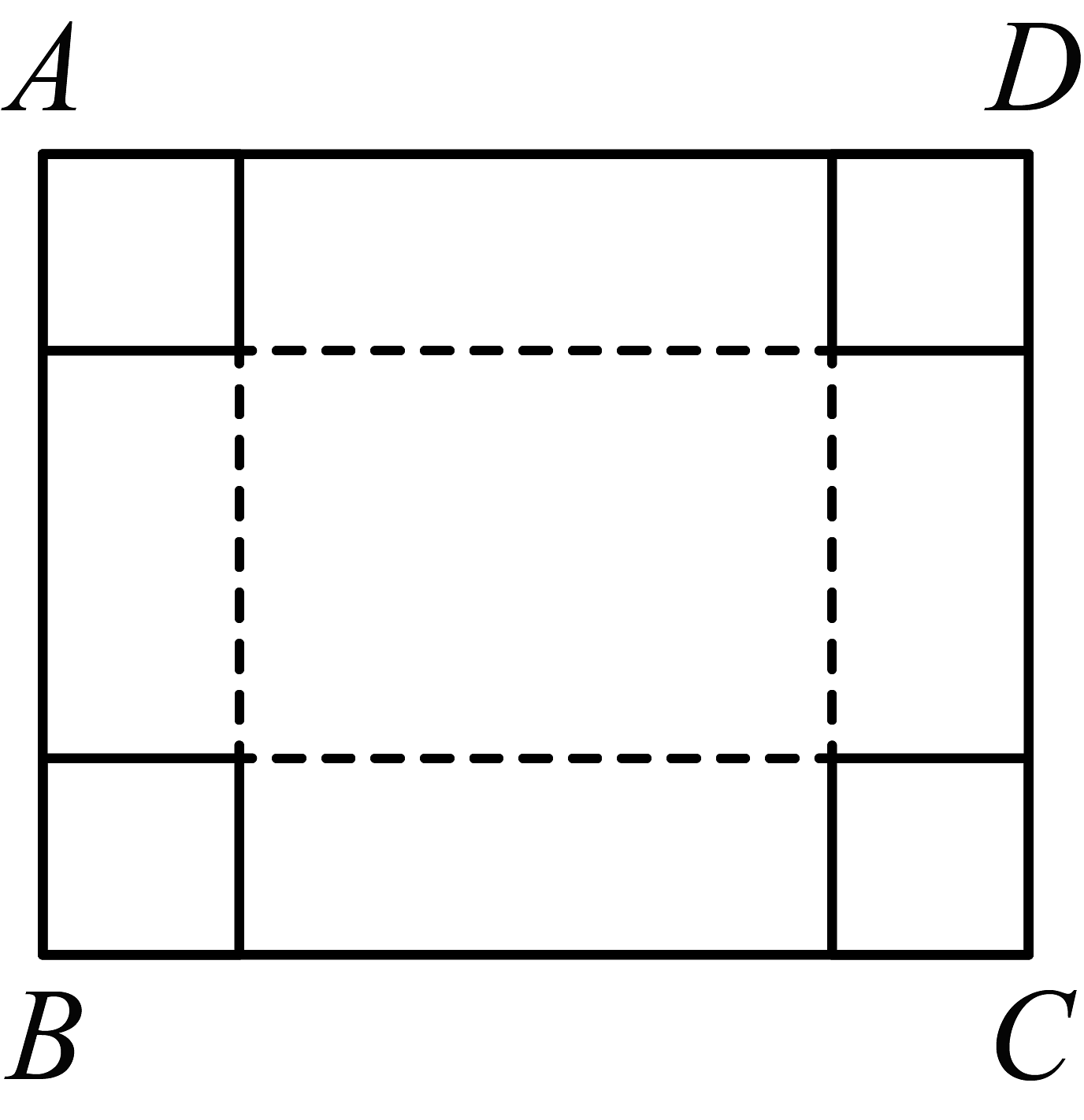(1)、如果剪去四个角剩下的纸片的面积为 $S_{1}$ ，请用含有x的式子表示 $S_{1}$ （结果要求化简）；

(2)、如图，沿虚线将剪去四个角剩下的纸片折成一个无盖的长方体纸盒，如果所得的长方体纸盒的体积是48立方厘米，求 $A D$ 的长．

查看解析
6、如图，线段 $A B ∥ C D$ ， $A D$ 与 $B C$ 交于点E．

(1)、求证： $A E \cdot C E = D E \cdot B E$ ；

(2)、过点E作 $E F ∥ C D$ ，交 $A C$ 于点F，如果 $E F = 2$ ， $C D = 3$ ，求 $A B$ 的长．

查看解析
7、中国古代有着辉煌的数学成就， $A$ ：《周髀算经》， $B$ ：《九章算术》， $C$ ：《海岛算经》， $D$ ：《孙子算经》等是我国古代数学的重要文献．

(1)、小聪想从这4部数学名著中随机选择1部阅读，则他选中《九章算术》的概率为___________；

(2)、某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容，求恰好选中 $A$ ：《周髀算经》和 $C$ ：《海岛算经》的概率．（用树状图或列表的方法）

查看解析
8、如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (3, 1), B (1, 2), C (4, 3)$ ．

(1)、以原点 $O$ 为位似中心，在第一象限内画出 $△ A B C$ 的位似图形 $△ A_{1} B_{1} C_{1}$ ，使它与 $△ A B C$ 的相似比为 $2 : 1$ ．

(2)、在（1）的条件下，若 $M (x, y)$ 为 $△ A B C$ 内部的一点，则点 $M$ 在 $△ A_{1} B_{1} C_{1}$ 内部的对应点 $M_{1}$ 的坐标为．

查看解析
9、如图，在 $△ A B G$ 中，C、E 和 D、F 分别是 $A G$ 、 $B G$ 的三等分点，且 $S_{△ G C D} = 6$ ，则 $S_{四边形 A B F E} =$ ．

查看解析
10、已知点 $C$ 是线段 $A B$ 的黄金分割点，若 $A B = 8$ ，则线段 $A C$ 的长为．

查看解析
11、已知 $x = - 2$ 是方程 $x^{2} - b x + c = 0$ 的一个根，则 $2 b + c$ 的值是（）

A、 $- 6$ B、6 C、4 D、 $- 4$

查看解析
12、任意抛掷一枚均匀的骰子两次，记两次朝上的点数的和为m，则下列m的值中，概率最大的是（）

A、6 B、7 C、8 D、9

查看解析
13、矩形具有而菱形不一定具有的性质是（）

A、对角相等 B、对边相等 C、对角线互相平分 D、对角线相等

查看解析
14、如图，在数轴上有A，B，M三点，分别表示有理数a，b，m．其中a，b，m满足 $|a + 1| + {(b - 2)}^{2} + |m - 3| = 0$ ．已知线段 $A B$ 的中点表示的数可以记作 $\frac{a + b}{2}$ ， A、B之间的距离为 $|a - b|$ ．

(1)、求a，b，m的值；

(2)、数轴上的一动点N从A出发，以2个单位长度/秒的速度向右运动，当N与B的距离为线段 $B M$ 长度的两倍时，求运动时间t，以及此时点N表示的数；

(3)、有一动点P从表示 $- 7$ 的点出发，以3个单位长度/秒的速度向右运动，动点Q从表示 $- 2$ 的点出发，以2个单位长度/秒的速度向右运动．点P比点Q先出发1秒，设点Q运动的时间为t秒，若线段 $P Q$ 上至少存在一点T与点A构成线段，当线段 $A T$ 的中点在线段 $O B$ （包含端点）上，求t最大值和最小值．

查看解析
15、观察下面三行数：
$- \frac{1}{2}$ 、 $\frac{1}{4}$ 、 $- \frac{1}{8}$ 、 $\frac{1}{16}$ 、 $- \frac{1}{32}$ ……；①
$- \frac{1}{4}$ 、 $\frac{1}{8}$ 、 $- \frac{1}{16}$ 、 $\frac{1}{32}$ 、 $- \frac{1}{64}$ ……；②
$\frac{1}{2}$ 、 $\frac{5}{4}$ 、 $\frac{7}{8}$ 、 $\frac{17}{16}$ 、 $\frac{31}{32}$ ……；③

(1)、第一行的第7个数可以表示为：______，第一行的第n个数可以表示为：______．

(2)、取每一行的第n个数，从上到下依次记作x、y、z，对于任意的正整数n均有， $x - a y + z$ 为一个定值，则 $a =$ ______．

(3)、是否存在这样的一列数，使得这样的一列三个数的和为 $\frac{123}{128}$ ？若存在，求出这一列数；若不存在，说明理由．

查看解析
16、某纸箱厂计划用20张白板纸制作某种型号的长方体纸箱，如图，每张白板纸有A，B，C三种剪裁方法，其中A种裁法：裁成4个侧面；B种裁法：裁成3个侧面与2个底面；C种裁法：裁成2个侧面与4个底面．已知四个侧面和两个底面恰好能做成一个纸箱．设按A种方法剪裁的白板纸有x张，按B种方法剪裁的白板纸有y张．（阴影部分为废料）

(1)、按C种方法剪裁的白板纸有______张．（用含x、y的式子表示）

(2)、将20张白板纸剪裁完后，裁出的侧面与底面一共有多少个？（用含x、y的式子表示，结果要化简）

(3)、请直接写出一种裁剪方案（三种裁法都要有），使得20张白纸板裁出的侧面和底面恰好可以全部配套做成长方体纸箱．并计算出可以做成______个纸箱．

查看解析
17、多项式 $\frac{1}{5} x^{2} + 3 x$ 与多项式A的和为 $- \frac{14}{5} x^{2} + 4 x$ ．式子 $A + t (5 x - 1)$ 不含一次项（t为常数）．

(1)、求多项式A．

(2)、求t的值．

查看解析
18、某快递站一名快递员以配送中心为基地，分别向东、西两方向各个小区送货，向东最远的洪林小区距离配送中心5000米，规定向东走为正，某一趟行程记录如下（单位：米） $+ 1500, - 320, - 430, + 2050, - 300, + 250, - 200, - 50, + 300, + 750, - 250$

(1)、他最终有没有到达洪林小区？如果没有，那么他离该小区还差多少米？

(2)、送货时，这名快递员全程都使用电动三轮车，且每米要消耗电动三轮车的电量0.85毫安时，问他共消耗了多少毫安时电量？（将结果用科学记数法表示．）

查看解析
19、（1）计算： $(\frac{1}{2} + \frac{3}{4} - \frac{1}{8}) \div \frac{1}{24}$ ；
（2）计算： ${(- 2)}^{3} - \frac{2}{5} \div 2 \times [- 2^{2} + {(- 3)}^{2}]$ ．

查看解析
20、（1）计算： $(- 8) + 10 + 2 - (- 7)$ ；
（2）计算： $\frac{1}{2} + (- \frac{2}{3}) + \frac{4}{5} + (- \frac{1}{3})$ ．

查看解析

上一页 992 993 994 995 996 下一页跳转