相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、如图,在中, , , 点在边上, , 点 , 在线段上, .
 (1)、求证:;(2)、若的面积为 , 的面积为 , 求的面积.
(1)、求证:;(2)、若的面积为 , 的面积为 , 求的面积. -
2、如图,点在四边形的内部,且点与点关于对称,交于点 , 点与点关于对称,交于点 , 分别交 , 于点 , .
 (1)、连接 , , 若 , 求的周长;(2)、若 , 求的度数.
(1)、连接 , , 若 , 求的周长;(2)、若 , 求的度数. -
3、如图,中, , 平分交于点D,E为线段上一点,连接 , 且 , 若 , , 求的长.

-
4、如图,在所给正方形网格(每个小正方格的边长均为1)中按要求完成下列各题.
 (1)、格点(顶点均在网格线的交点上)的面积为_____;(2)、画出格点关于直线对称的(点 , , 的对应点分别为 , , ).
(1)、格点(顶点均在网格线的交点上)的面积为_____;(2)、画出格点关于直线对称的(点 , , 的对应点分别为 , , ). -
5、如图,在中, , 分别垂直平分和 , 交于 , 两点.与相交于点 . 连接 , , .

(1)若的周长为 , 的周长为 , 则的长为 , 的长为;
(2)若 , 则的度数为 .
-
6、如图.已知 . 点E,F在边上.点G,H在边上,分别沿 , 折叠,使点和点都落在点处,若 , , 则的度数为 , 的度数为 .

-
7、如图,中,是延长线上一点, , 过点作且 , 连接并延长,分别交 , 点 , . 若 , , 则的度数为°

-
8、如图所示的方格中, .
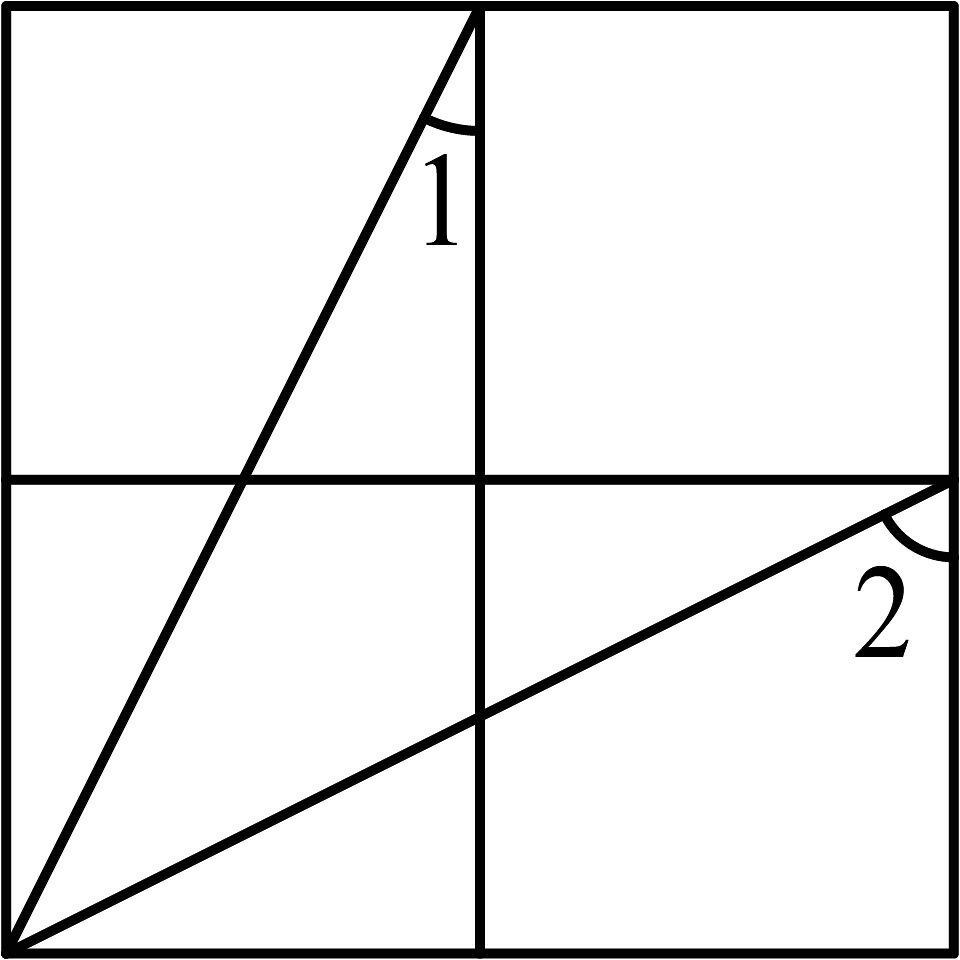
-
9、如图,等腰的底边长为6,面积是36,腰的垂直平分线分别交边于E,F两点若点为边的中点,点为线段上一动点,则周长的最小值为( )
 A、16 B、15 C、12 D、10
A、16 B、15 C、12 D、10 -
10、如图,在中, , 将沿直线m翻折,点B落在点D的位置,则的度数是( )度.
 A、68 B、58 C、34 D、17
A、68 B、58 C、34 D、17 -
11、下列消防标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
12、如图,点和点把线段分成三部分,点是线段的中点, , 求线段的长 .

-
13、如图,二次函数的图象与x轴的交点分别为和 , 与y轴交于点C,Q是直线上方二次函数图象上一动点.
 (1)、求二次函数的解析式.(2)、如图1,过点Q作x轴的平行线交于点E,过点Q作y轴的平行线交x轴于点D,求的最大值及点Q的坐标.(3)、如图2,设M为抛物线对称轴上一动点,当点Q,点M运动时,在坐标轴上确定点N,使四边形为矩形,求出所有符合条件的点N的坐标.
(1)、求二次函数的解析式.(2)、如图1,过点Q作x轴的平行线交于点E,过点Q作y轴的平行线交x轴于点D,求的最大值及点Q的坐标.(3)、如图2,设M为抛物线对称轴上一动点,当点Q,点M运动时,在坐标轴上确定点N,使四边形为矩形,求出所有符合条件的点N的坐标. -
14、如图,在平面直角坐标系中,已知 , . 动点M从点A出发,沿向终点O方向运动,动点N从点O出发,沿向终点B方向运动,如果点M的速度是每秒4个单位长度,点N的速度是每秒2个单位长度,它们同时出发,当有一点到达终点时,两点均停止运动.设运动时间为 .
 (1)、当时,求M,N两点之间的距离.(2)、用含t的代数式表示的面积S.(3)、当为多少时,以O,M,N为顶点的三角形与相似?
(1)、当时,求M,N两点之间的距离.(2)、用含t的代数式表示的面积S.(3)、当为多少时,以O,M,N为顶点的三角形与相似? -
15、综合与实践
【问题情境】图1是喷水管从点A向四周喷出水花的喷泉,喷出的水花是形状相同的抛物线.如图2,以点O为原点,建立平面直角坐标系,水平方向为x轴,所在直线为y轴,点C、D为水花的落水点在x轴上,抛物线的解析式为 .

【问题解决】
(1)、求喷水管的高度;(2)、现重新改建喷泉,降低喷水管,使落水点与喷水管的水平距离为 , 已知喷水管降低后,喷水管喷出的水花抛物线形状不改变,且水柱在距原点的水平距离处达到最高,求喷水管要降低的高度. -
16、如图,在中, , , , 点Q在边上, , 点P在边上, , 垂足为H.
 (1)、求证: .(2)、求的长.
(1)、求证: .(2)、求的长. -
17、如图,已知反比例函数的图象与直线相交于 , B两点.
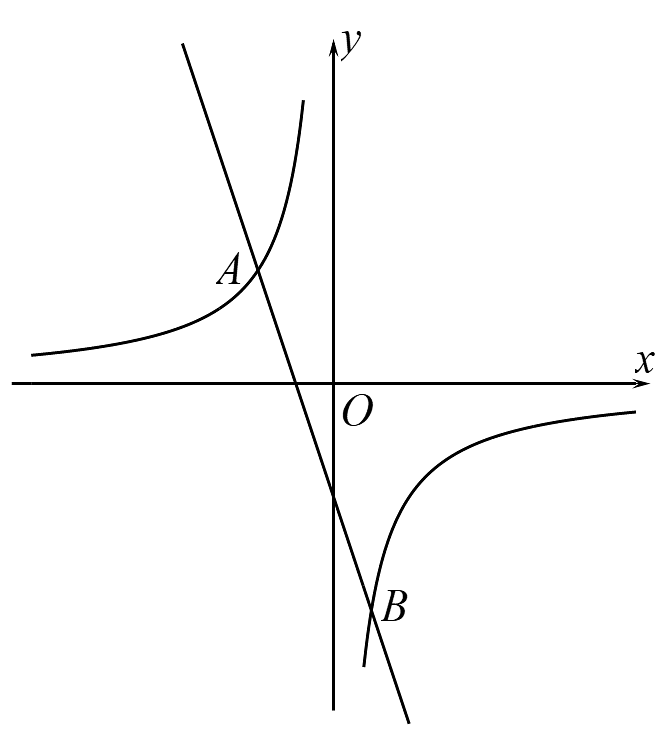 (1)、求k的值.(2)、当时,请直接写出x的取值范围.
(1)、求k的值.(2)、当时,请直接写出x的取值范围. -
18、定义:在平面直角坐标系中,横、纵坐标相等的点为“完美点”,顶点是“完美点”的二次函数为“完美函数”.(1)、若点是“完美点”,求a的值.(2)、已知某“完美函数”的顶点在直线上,且与y轴的交点到原点的距离为4,求该“完美函数”的解析式.
-
19、杠杆原理也称为“杠杆平衡条件”,要使杠杆平衡,作用在杠杆上两个力矩(力与力臂的乘积)大小必须相等,即:阻力阻力臂动力动力臂,用代数式表示为 . 如图,已知石头重量(阻力)为 , 阻力臂长 , 小华想用一根撬棍撬起这块石头,但他只有的力量,那么他该选择动力臂为多少米的撬棍才能撬动这块大石头?

-
20、如图,在边长为1个单位长度的小正方形组成的网格中,建立平面直角坐标系 , 的三个顶点A,B,C都在格点(网格线的交点)上.
 (1)、将向左平移6个单位长度,得到 , 画出 .(2)、画出与相似的 , 使它与的相似比为 .
(1)、将向左平移6个单位长度,得到 , 画出 .(2)、画出与相似的 , 使它与的相似比为 .