相关试卷

1、如图， AC=AD， AB 平分∠CAD，求证∠C=∠D.

查看解析
2、如图，在△ABC中， AD 是它的角平分线， DE∥AC， DE交 AB 于点 E， DF∥AB， DF 交 AC 于点 F.图中∠1与∠2有什么关系?为什么?

查看解析
3、如图，在△ABC 中，若 AB =2， BC =4，则△ABC 的高AD 与CE 的比是多少?（提示：利用三角形的面积公式.）

查看解析
4、

(1)、已知等腰三角形的一边长为5，一边长为6，求它的周长；

(2)、已知等腰三角形的一边长为4，一边长为9，求它的周长.

查看解析
5、一个等腰三角形的一边长为6，周长为20，求其他两边的长.

查看解析
6、如图，在△ABC 中， AE 是中线， AD 是角平分线， AF 是高. 填空：

(1)、 $B E =$ = $\frac{1}{2}$

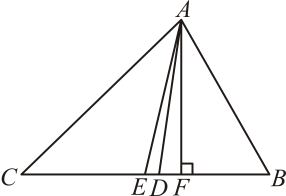(2)、 $∠ B A D =$ = $\frac{1}{2}$

(3)、∠AFB==90°；

(4)、若BC=8， AF=5，
则S△ABC= ， S△ABE=.

查看解析
7、对于下面每个三角形，分别过顶点 A 画出它的中线、角平分线和高.

查看解析
8、长为100 cm， 70 cm， 50cm， 30cm的四根木条，选其中三根组成三角形，有几种选法?为什么?

查看解析
9、三角形的三边长分别为2，7，a，则a的取值范围是.

查看解析
10、填空题.

(1)、如图（1）， AD，BE，CF 是△ABC的三条中线，则BD= ， $A E =$ $\frac{1}{2}$ ， $A B =$

(2)、如图（2）， AD， BE，CF 是△ABC的三条角平分线，则∠1= ， ∠3= $\frac{1}{2}$ ， ∠ACB=2.

查看解析
11、如图，过△ABC的顶点C分别画出它的中线、角平分线和高.

查看解析
12、一根4dm长的木条和两根1dm长的木条，能否组成一个等腰三角形?
两根4d m长的木条和一根1 dm长的木条呢?

查看解析
13、下列长度的三条线段能否组成三角形?为什么?

(1)、3， 4， 8；

(2)、5， 6， 11；

(3)、5， 6， 10.

查看解析
14、用一条长为18 cm的细绳围成一个等腰三角形.

(1)、如果腰长是底边长的2倍，那么各边的长是多少?

(2)、能围成有一边的长是4 cm的等腰三角形吗?为什么?

查看解析
15、中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录，下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”，其中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看解析
16、数轴是数学学习的一个很重要的工具，利用数轴可以将数与形完美结合 $.$ 研究数轴我们可发现许多重要的规律：
①绝对值的几何意义：一般地，若点A、点B在数轴上表示的数分别为a，b，那么A、B两点之间的距离表示为 $|a - b|$ ，记作 $A B = |a - b|$ ， $|3 - 1|$ 则表示数3和1在数轴上对应的两点之间的距离；又如 $|3 + 1 |=| 3 - (- 1)|$ ，所以 $|3 + 1|$ 表示数3和 $- 1$ 在数轴上对应的两点之间的距离；
②若数轴上点A、点B表示的数分别为a、b，那么线段 $A B$ 的中点M表示的数为 $\frac{a + b}{2}$ ．
请借用数轴和以上规律解决下列问题：
如图，已知数轴上有A、B两点，分别表示的数为 $- 10$ ， 6，点P以每秒2个单位长度的速度从点A出发沿数轴向右匀速运动，点Q以每秒1个单位长度从点B出发沿数轴向左匀速运动，当一个点到达终点，另一个点也随之停止运动，设运动时间为t秒 $(t > 0)$ ．

(1)、A、B两点的距离为______个单位长度；线段 $A B$ 的中点M所表示的数为______；

(2)、点P运动t秒后所在位置的点表示的数为______；点Q运动t秒后所在位置的点表示的数为______．（用含t的式子表示）

(3)、P、Q两点经过多少秒会相距5个单位长度？

(4)、在点P、Q运动过程中，O、P、Q三点有一点恰好是以另两点为端点的线段的中点时，直接写出此时t的值．

查看解析
17、对于有理数a、b，定义运算： $a \otimes b = a b + |a| - b$ ．

(1)、填空： $3 \otimes (- 2)$ ________ $(- 2) \otimes 3$ （填“ $>$ ”“ $<$ ”或“ $=$ ”）；

(2)、若m与 $- \frac{1}{5}$ 互为倒数，n与 $- 4$ 互为相反数，求 $m \otimes n$ 的值；

(3)、求 $[2 \otimes (- 3)] \otimes 4$ 的值．

查看解析
18、已知 $|a| = 2$ ， $|b| = 3$ ，且 $a b < 0$ ，求 $a - 2 b$ 的值．

查看解析
19、如图，数轴上每个刻度为1个单位长度，点A表示的数是 $- 4$ ．

(1)、在数轴上标出原点，把数轴补充完整，点B所表示的数是________；

(2)、在数轴上找一点C，使它与点B的距离为3个单位长度，那么点C表示的数为________；

(3)、在数轴上表示数 $2.5$ ， $- 4 \frac{1}{2}$ ， 0， $- |2|$ ， $- (- 5)$ ，并用“<”号把这些数按从小到大连接起来．

查看解析
20、计算：

(1)、 $- 4 - (- 3) - (+ 2) + (- 6)$

(2)、 $(\frac{7}{4} - \frac{7}{8} - \frac{7}{12}) \div (- \frac{7}{8}) + (- \frac{8}{3})$

(3)、 $(- 1) + {(- 2)}^{2} \times 3 - 8 + (- 2)$

(4)、 $- 1^{4} - |0.5 - \frac{2}{3}| \div \frac{1}{3} \times [- 2 - {(- 3)}^{2}]$

查看解析

上一页 816 817 818 819 820 下一页跳转