相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
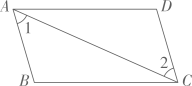
1、 如图, ∠1=∠2, ∠B=∠D. 求证AB=CD.
-
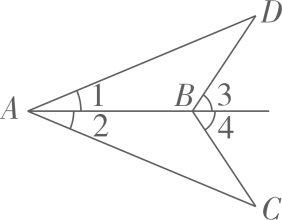
2、 如图, ∠1=∠2, ∠3=∠4. 求证 AC=AD.
-
3、如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).在图中,要测量工件内槽宽AB,只需要测量哪些量?为什么?

-
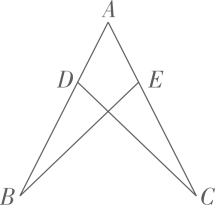
4、 如图, AB=AC, AD=AE, 求证∠B=∠C.
-
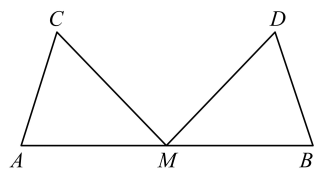
5、 如图, M是AB 的中点, ∠AMC=∠BMD, MC=MD. 求证AC=BD.
-
6、 如图, AB=CD, AE⊥BC, DF⊥BC, 垂足分别为E, F, CE=BF.求证AE=DF.

-
7、如图,C是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走, 并同时到达D, E 两地, 且 DA⊥AB, EB⊥AB.D,E到路段AB 的距离相等吗?为什么?

-
8、如图, AC⊥BC, BD⊥AD, 垂足分别为C, D, AC=BD. 求证BC=AD.

-
9、如图,用直尺和圆规作一个三角形,使这个三角形的两角分别等于∠α,∠β,这两角的夹边等于线段a.

-
10、如图,用直尺和圆规作一条直线,使这条直线过△ABC 的顶点A,并且与边 BC 平行.

-
11、 如图, 已知线段a, b和∠α, 求作△ABC, 使AB=a,AC=b, ∠A=∠α.

-
12、如图,已知直线AB 及直线AB 外一点C.利用直尺和圆规过点C 作直线AB 的平行线CD.

-
13、工人师傅常用角尺平分一个任意角.如图,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合.过角尺顶点C的射线OC 便是∠AOB 的平分线.为什么?

-
14、 如图, AC=BD, BC=AD. 求证∠ABC=∠BAD.

-
15、在如图14.2-14所示的三角形钢架中, AB=AC, AD 是连接点A与BC 中点 D 的支架. 求证AD⊥BC.

-
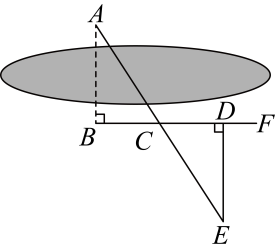
16、如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD, 再画出BF的垂线DE,使点E与点A,C在一条直线上,这时测得DE的长就是AB 的长.为什么?
-
17、 如图, AB⊥BC, AD⊥DC, 垂足分别为B, D, 且∠1=∠2. 求证AB=AD.

-
18、如图14.2-8, 点D 在AB 上, 点E 在AC上, AB=AC,∠B=∠C. 求证AD=AE.

-
19、 如图, 点E,F在BC上, BE=CF,AB=DC,∠B=∠C. 求证∠A=∠D.

-
20、如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A 和点B.连接AC 并延长到点D, 使CD=CA.连接BC 并延长到点E, 使CE=CB.连接DE,那么量出 DE的长就是A,B的距离.为什么?
