相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、已知二次函数的自变量与函数的部分对应值列表如下,则方程的解是 .
…
0
…
…
3
…
-
2、二次函数的部分图象如图所示,图象过点 , 对称轴为直线 , 下列结论:(1);(2);(3);(4)若点 , 点 , 点在该函数图象上,则 , 其中正确的结论有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个 -
3、如图,半径为10的⊙中,弦 , 所对的圆心角分别是 , . 已知 , , 则点到的距离等于( )
 A、8 B、6 C、 D、
A、8 B、6 C、 D、 -
4、如图,已知点 , , 与关于轴对称,连接 , 现将线段以点为中心顺时针旋转得 , 点的对应点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、关于的一元二次方程有实数根,则的取值范围是( )A、 B、且 C、 D、且
-
6、下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
7、在平面直角坐标系中,直线与x轴、y轴分别相交于A、B两点,C为的中点,点D在线段上(),连接 , 将绕点C逆时针旋转得到 , 旋转角为(),连接 , .
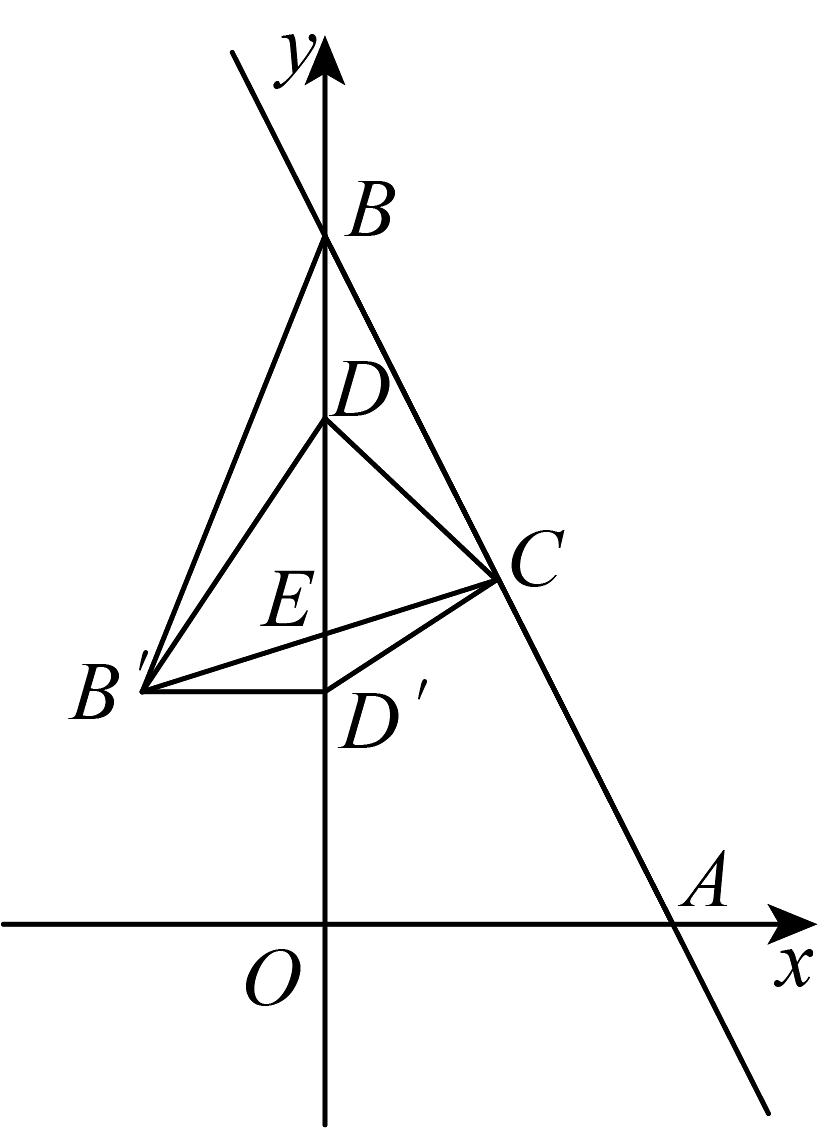 (1)、求的值;(2)、如图,当点恰好落在y轴上时,交y轴于点E,求证:;(3)、当点D的坐标为 , 且时,求点的坐标.
(1)、求的值;(2)、如图,当点恰好落在y轴上时,交y轴于点E,求证:;(3)、当点D的坐标为 , 且时,求点的坐标. -
8、【问题背景】
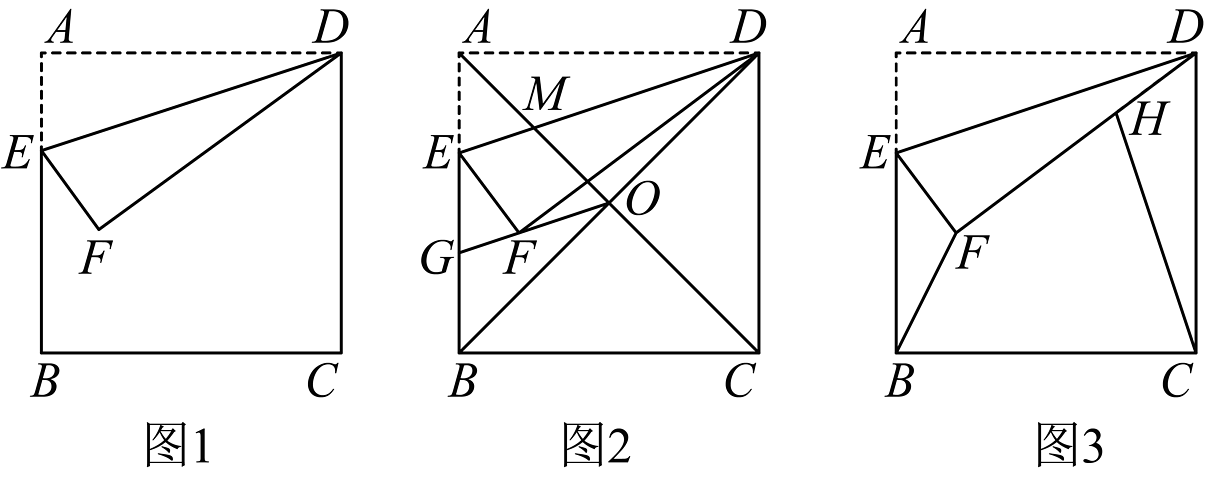
如图1,已知正方形的边长为3,点E是边上的一点,把沿直线对折后,点A落在点F处.
【问题探究】
(1)如图2,当时,正方形的对角线与相交于点M,与正方形另一条对角线相交于点O,连接并延长,交线段于点G.
①求的值,并说明点M是的中点;
②试探究与有怎样的位置关系,并说明理由.
【拓展延伸】
(2)如图3,点H是线段上的一点,且 , 连接、 . 在点E从点A运动到点B的过程中,求的最小值.
-
9、如图,在中, , , . 点D从点C出发沿方向以每秒个单位长的速度向点B匀速运动,同时点E从点A出发沿方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒().过点D作交于点F,连接、 .
 (1)、用t表示_______,________,________.(2)、是否存在某一时刻使四边形成为菱形?如果能,求出相应的t值;如果不能,说明理由;
(1)、用t表示_______,________,________.(2)、是否存在某一时刻使四边形成为菱形?如果能,求出相应的t值;如果不能,说明理由; -
10、如图,在菱形中,对角线 , 交于点O,过点A作于点F,延长到点E,使得 , 连接 .
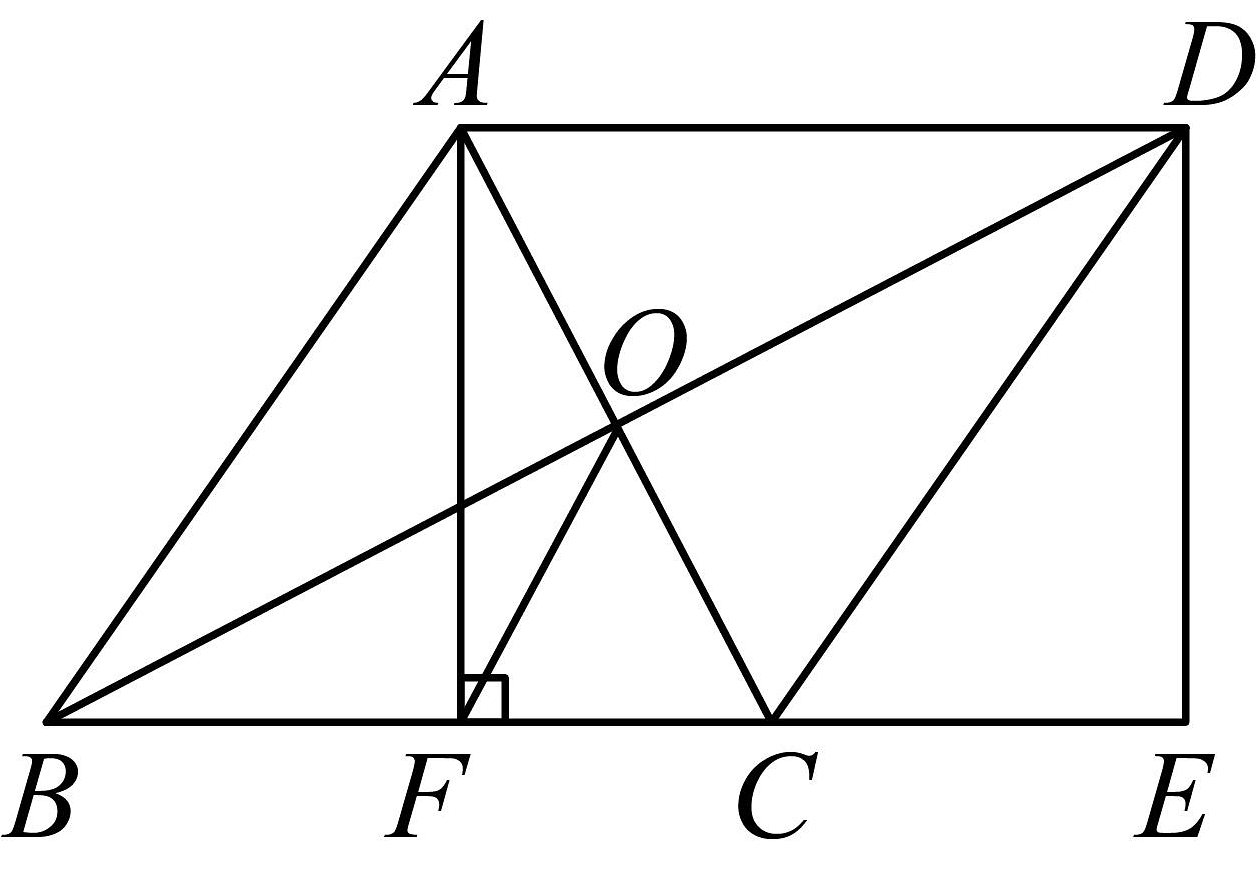 (1)、求证:四边形是矩形;(2)、连接 , 若 , , 求的长.
(1)、求证:四边形是矩形;(2)、连接 , 若 , , 求的长. -
11、某工厂生产一批小家电,2022年的出厂价是144元,2023年,2024年连续两年改进技术,降低成本,2024年出厂价调整为100元.(1)、如果这两年出厂价下降的百分比相同,求平均下降率.(百分数小数点后保留两位小数)(2)、某商场今年销售这批小家电的售价为140元时,平均每天可销售20台,为了减少库存,商场决定降价销售,经调查发现小家电单价每降低5元,每天可多售出10台,如果每天盈利1200元,单价应降低多少元?当降价多少元时,每天可以获得最大利润?最大利润是多少?
-
12、某市利用各类灵活多样的宣传方式、各种宣传载体,全方位开展“国家反诈中心” 宣传推广工作,截至2023年底,注册人数已达216.39万人,某社区工作人员为调 查本社区居民对于“国家反诈中心”的了解情况,进行了一次问卷调查,本次问卷共设置10个问题,每题10分,问卷调查结束后,根据问卷结果分为A:非常了解(80-100分)、B:比较了解(60-80分)、C:基本了解(40-60分)、D:不太了解(0-40分)
四个等级并绘制了如下两幅不完整的统计图.
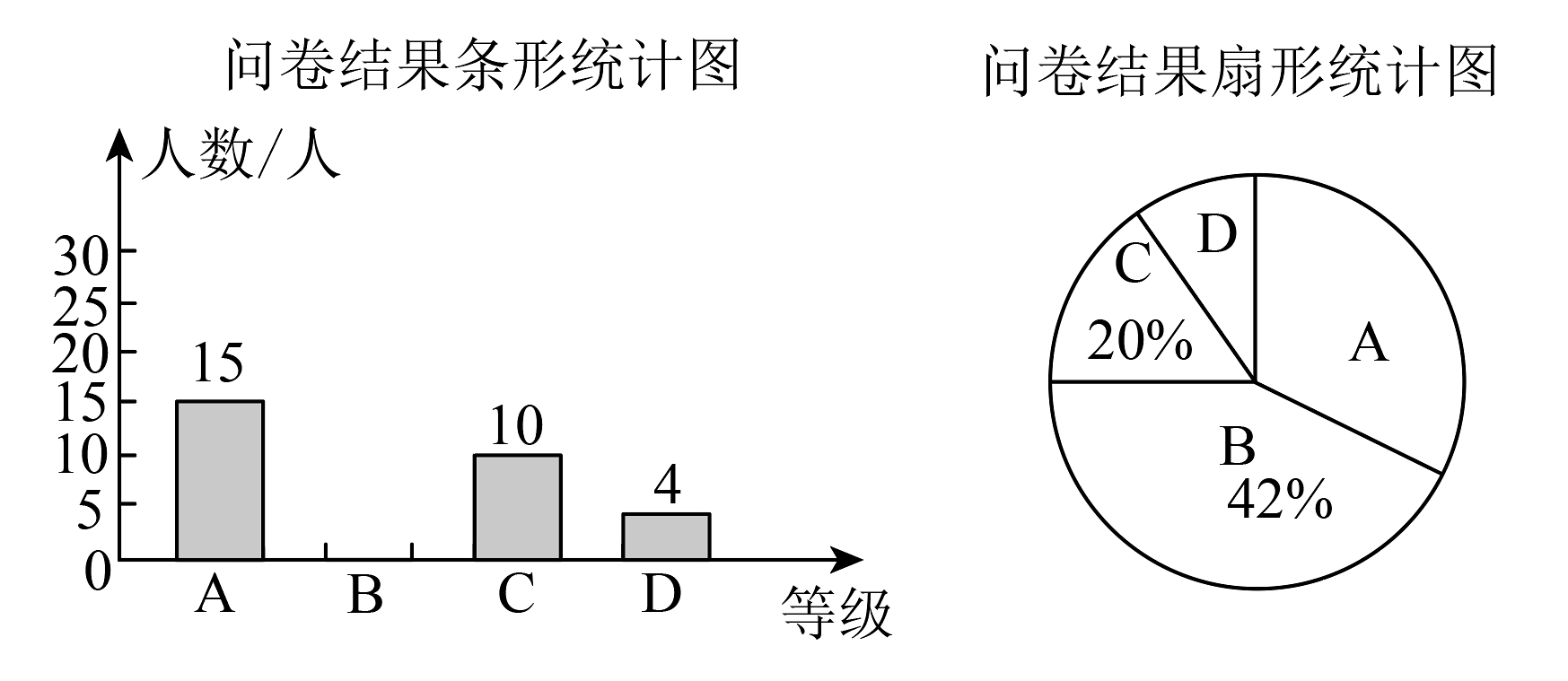
请根据如图提供的信息解答下列问题:
(1)、扇形统计图中,A等级对应的扇形的圆心角度数为________,补全条形统计图;(2)、若该社区共有居民8000人,请你估计对于“国家反诈中心”非常了解的人数;(3)、为更好地开展“国家反诈中心”宣传推广工作,社区准备招募2名宜讲人员,现有问卷结果等级为A的4人报名,其中3人为一组居民,1人为二组居民,若从中随机选取2人,求选取的2人不是同一组居民的概率. -
13、已知a,b是方程的两个实数根,则的值是 .
-
14、黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性,蕴藏着丰富的美学价值.如图,某校艺术节“达人秀”活动舞台的长为16米,主持人站在点C处自然得体(点C是线段靠近点B的黄金分割点),此时主持人与点A的距离是米;
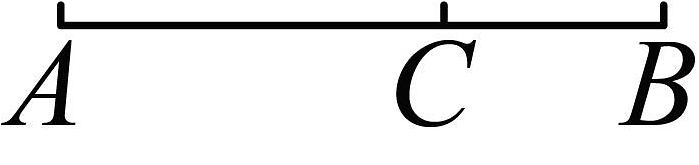
-
15、如果 , 那么的值为 .
-
16、如图,已知正方形 , E为的中点,F是边上的一个动点,连接将沿折叠得 , 延长交于M,现在有如下5个结论:①一定是直角三角形;②;③当M与C重合时,有;④平分正方形的面积;⑤ , 在以上5个结论中,其中正确的结论个数是( )
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5 -
17、如图,AD是△ABC的中线,E是AC边上一点,且CE:AE=1:2,BE交AD于点F,则AF:FD为( )
 A、5:1 B、4:1 C、3:1 D、2:1
A、5:1 B、4:1 C、3:1 D、2:1 -
18、如图中, , 延长至点A,使 , 连结 , 此时 . 则的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、定义:我们把一次函数的图象与正比例函数的图象的交点称为一次函数图象的“亮点”.例如:求一次函数图象的“亮点”时,联立方程得 , 解得 , 则一次函数图象的“亮点”为 .(1)、一次函数图象的“亮点”为 ;(2)、一次函数图象的“亮点”为 , 求m,n的值;(3)、若一次函数的图象分别与x轴,y轴交于点A,B,且一次函数的图象上没有“亮点”,点P在y轴上, , 直接写出满足条件的点P的坐标.
-
20、如图,中,于点D, , 点E在上, , 连接 .
 (1)、求证: ;(2)、延长交于点F,连接 , 求的度数;(3)、过点C作 , , 连接交于点N,若 , , 直接写出的面积 .
(1)、求证: ;(2)、延长交于点F,连接 , 求的度数;(3)、过点C作 , , 连接交于点N,若 , , 直接写出的面积 .