相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、n边形的每个内角都为 , 则边数n为( )A、13 B、14 C、15 D、16
-
2、在等边中,线段 为边上的高,点 D 是直线 上 的一个动点,以为一边,在的下方作等边 , 连接 .
 (1)、填空:如图① , 当点 D 在线段上时,(2)、如图② ,当点D在线段的反向延长线上时,求的度数;
(1)、填空:如图① , 当点 D 在线段上时,(2)、如图② ,当点D在线段的反向延长线上时,求的度数; -
3、如图,点C在线段上, , , , 平分 .
 (1)、求证:;(2)、请你写出与的位置关系,并说明理由.
(1)、求证:;(2)、请你写出与的位置关系,并说明理由. -
4、如图1,在中,是的角平分线;
 (1)、填写下面的表格.
(1)、填写下面的表格.的度数
的度数
(2)、试猜想与之间存在一个怎样的数量关系,并证明你的猜想; -
5、如图,△ABC在平面直角坐标系中,点A, B ,C的坐标分别为 .
 (1)、作出关于y 轴对称的;(2)、写出三点的坐标 , , ;(3)、请写出点关于直线n(直线n上各点的纵坐标都为)对称的点的坐标 .
(1)、作出关于y 轴对称的;(2)、写出三点的坐标 , , ;(3)、请写出点关于直线n(直线n上各点的纵坐标都为)对称的点的坐标 . -
6、如图, , , 要使 , 则应补充条件:(填写一个即可).

-
7、若等腰三角形的一个角是 , 它的另外两个角的度数分别是 .
-
8、如图所示, , , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9、在平面直角坐标系中,点关于y轴对称的点的坐标是( ).A、 B、 C、 D、
-
10、若正多边形的内角和是 , 则该正多边形的一个外角是( )A、 B、 C、 D、
-
11、在中, , , 则的度数为( )A、 B、 C、 D、
-
12、如图,是正方形内一点,将绕点顺时针方向旋转得到 .
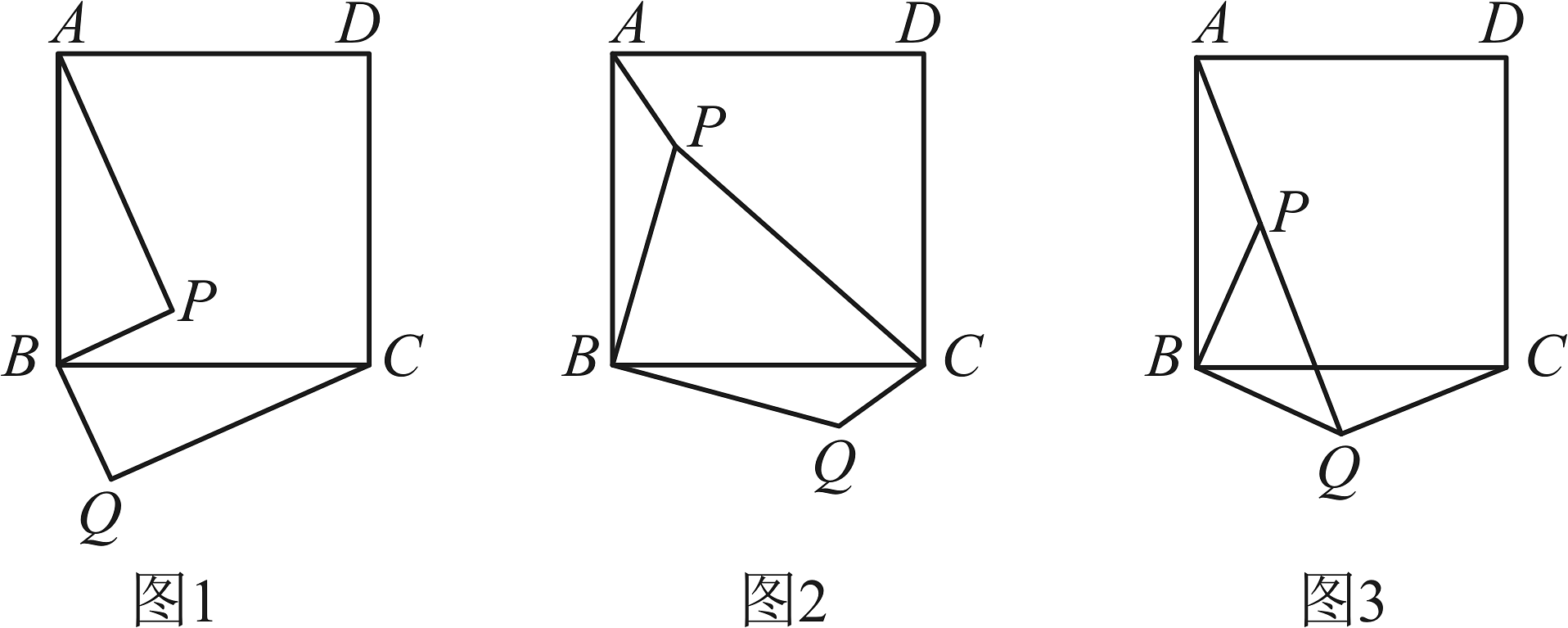 (1)、观察猜想:如图1,线段与的数量关系是______,位置关系是______.(2)、探究实践:如图2,连接 , 若 , , , 求的度数.(3)、拓展延伸:如图3,A,P,Q三点在一条直线上,若 , , 请求出的长度.
(1)、观察猜想:如图1,线段与的数量关系是______,位置关系是______.(2)、探究实践:如图2,连接 , 若 , , , 求的度数.(3)、拓展延伸:如图3,A,P,Q三点在一条直线上,若 , , 请求出的长度. -
13、如图,是的弦,半径 , 垂足为H, , 交延长线于点C.
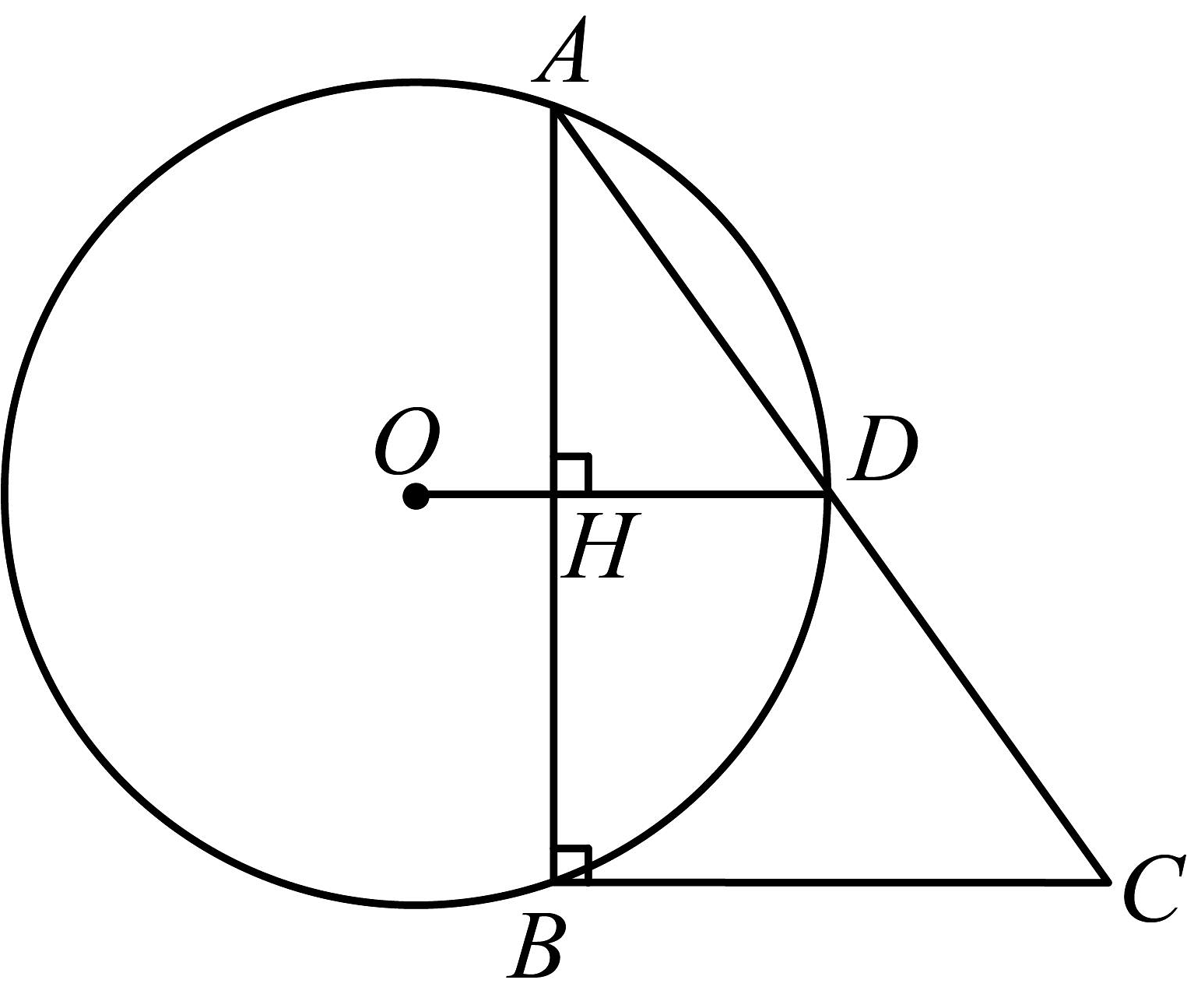 (1)、求证:D是的中点;(2)、若 , , 求的半径.
(1)、求证:D是的中点;(2)、若 , , 求的半径. -
14、解方程:(1)、;(2)、 .
-
15、在平面直角坐标系中,点绕原点顺时针旋转所得点的坐标是 .
-
16、已知一元二次方程的一个根为 , 则c的值为 .
-
17、如图,的直径与弦的延长线交于点 , 若 , , 则等于( )
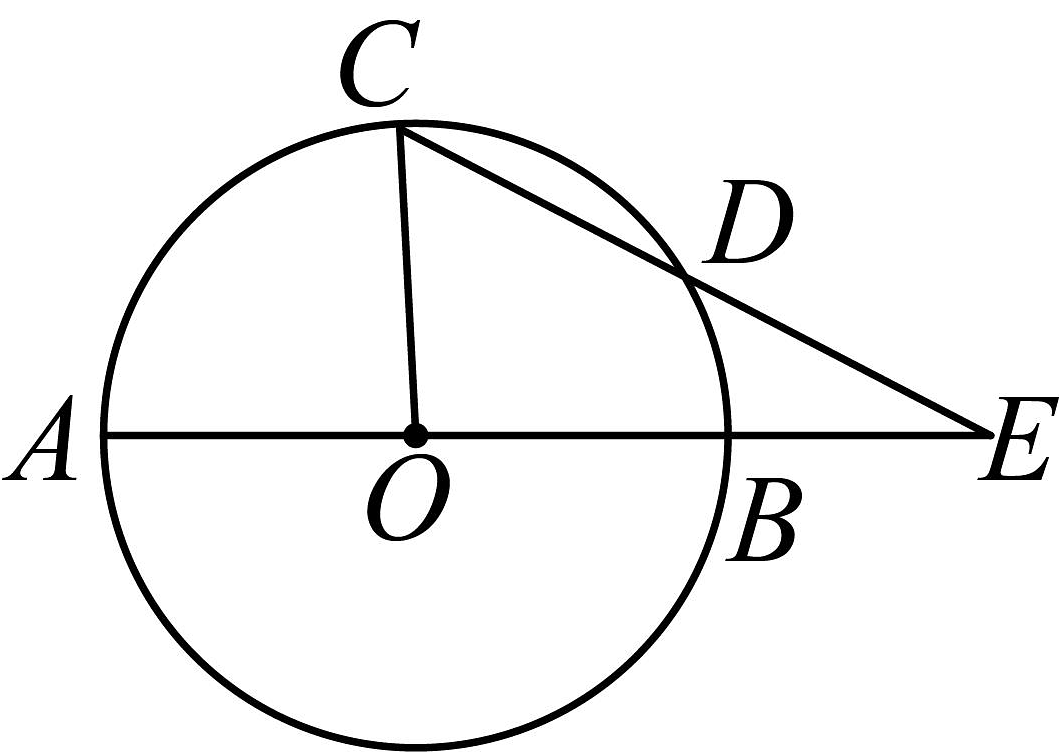 A、 B、 C、 D、
A、 B、 C、 D、 -
18、下列语句中:①直径是弦,弦是直径;②平分弦的直径垂直于弦;③长度相等的弧是等弧;④经过圆心的每一条直线都是圆的对称轴;⑤相等的圆心角所对的弧度数相等.其中正确的个数是( )A、1个 B、2个 C、3个 D、4个
-
19、在平面直角坐标系中,点A,B在坐标轴上, , . 点C为的中点,D为上一点.
 (1)、如图(1),将线段绕点A逆时针旋转 , 得到线段 .
(1)、如图(1),将线段绕点A逆时针旋转 , 得到线段 .①求证: .
②P为x轴上一点,且在点D左侧,点D关于点P对称的点为Q,连接 , . 是否存在这样的点P,使得对于任意的点D,总有成立?若存在,请写出P的坐标,并证明;若不存在,请说明理由.
(2)、如图(2),过点C作的垂线,交y轴于点F.连接 , . 若 , 请写出 , , 的数量关系,并证明. -
20、如图,在等边中,点D为边上一点,将沿翻折得到 , 连接并延长,交的延长线于点F.
 (1)、求的度数;(2)、过点D作交于点G,连接交于点H,求证: .(3)、若 , , 则的长为______(用含a,b的式子表示).
(1)、求的度数;(2)、过点D作交于点G,连接交于点H,求证: .(3)、若 , , 则的长为______(用含a,b的式子表示).